Física molecular
La ionización es el fenómeno químico o físico mediante el cual se producen iones, estos son átomos o moléculas cargadas eléctricamente debido al exceso o falta de electrones respecto a un átomo o molécula neutra. A la especie química con más electrones que el átomo o molécula neutros se le llama anión, y posee una carga neta negativa, y a la que tiene menos electrones catión, teniendo una carga neta positiva. Hay varias maneras por las que se pueden formar iones de átomos o moléculas.
Química
En ciertas reacciones químicas la ionización ocurre por transferencia de electrones; por ejemplo, el cloro reacciona con el sodio para formar cloruro de sodio, que consiste en iones de sodio (Na+) e iones de cloruro (Cl-). La condición para que se formen iones en reacciones químicas suele ser una fuerte diferencia deelectronegatividad entre los elementos que reaccionan o por efectos de resonancia que estabilizan la carga. Además la ionización es favorecida por medios polares que consiguen estabilizar los iones. Así el pentacloruro de fósforo (PCl5) tiene forma molecular no iónica en medios poco polares como el tolueno y disocia en iones endisolventes polares como el nitrobenceno (O2NC6H5).
La presencia de ácidos de Lewis como en los haluros de aluminio o el trifluoruro de boro (BF3) también puede favorecer la ionización debido a la formación de complejos estables como el [AlCl4-]. Así la adición de tricloruro de aluminio a una disolución del cloruro de tritl (Cl-CPh3), un compuesto orgánico, resulta en la formación del tetracloroaluminato de tritilio ([AlCl4]-[CPh3]+), una sustancia iónica y la adición de cloruro de alumino a tetraclorociclopropeno (C3Cl4, un líquido orgánico volátil) proporciona el tetracloroaluminato de triclorociclopropenilio ([AlCl4]-[C3Cl3]+) como sólido incoloro. A este proceso se le suman las umas de los electrones compuestos por menos cargas negativas al núcleo del primer átomo consecutivo.
Física
En el ambiente (aire, agua, suelo, etc.) existen microorganismos o microbios que contaminan, aprovechando los nutrientes a su alcance para desarrollarse o permanecer en ellos.
La esterilización es la práctica que tiene por fin destruir o eliminar todos los microbios. El efecto bactericida de las radiaciones es conocido desde tiempos antiguos como la era de hielo, así por ejemplo se sabe que la radiación solar, o más precisamente las radiaciones ultravioletas, son agentes naturales de esterilización.Sin embargo, las radiaciones electromagnéticas infrarrojas son las menos eficaces debido a su gran longitud de onda. La esterilización mediante rayos gamma es una tecnología que ha sido identificada como una alternativa segura para reducir la carga microbiana en alimentos y en insumos que entran en contacto directo con ellos, reduciendo el riesgo de contagio de enfermedades transmitidas por alimentos, en la producción, procesamiento, manipulación y preparación de éstos, todo lo cuál aumenta la calidad y competitividad de los productos otorgándoles un mayor valor añadido.
La energía ionizante se puede originar a partir de tres fuentes distintas: rayos gamma, una máquina generadora de electrones y rayos X. La fuente más común de losrayos gamma es el cobalto-60.
Los rayos gamma se componen de ondas electromagnéticas de longitud de onda muy cortas que penetran en los envases y productos expuestos a dicha fuente, ocasionando pequeños cambios estructurales en la cadena de ADN de las bacterias o microorganismos, causándoles la muerte o dejándolas inviables o estériles, sin capacidad de replicarse. La tecnología permite el tratamiento de los productos en su envase final.
La energía ionizante es factible de ser aplicada a una gran variedad de productos, con el fin de esterilización o reducción de carga microbiana, eliminando patógenos que pueden ser dañinos para la salud. Entre los productos tratados se encuentran: Alimentos, cosméticos, productos médicos, hierbas medicinales, productos de laboratorio y farmacéutico, alimento animal y embalajes.
La tecnología existe en forma comercial desde la década de 1950 y está autorizada su uso en más de treinta países, para más de cincuenta productos alimentarios. Cuenta con la aprobación de importantes organismos internacionales como: la WHO, FAO y la IAEA. También cuenta con la aprobación de la FDA, que plasma su normativa en el código 21 CFR 179.26. Estas entidades pueden recomendar, regular o legislar sobre la correcta aplicación de la tecnología, estableciendo los parámetros adecuados de operación y las dosis máximas aplicables a cada tipo de producto.
- WHO (World Health Organization) Organización Mundial de la Salud.
- IAEA (International Atomic Energy Agency) organismo autónomo que promueve el uso pacífico de la energía nuclear (en español: OIEA, Organización Internacional de Energía Atómica).
- FDA (Food and Drug Administration) Agencia de gobierno de los EEUU que regula alimentos y productos farmacéuticos.
- FAO (Food and Agriculture Organization) Organización de las Naciones Unidas para la Agricultura y la Alimentación.
Los rayos gamma no dejan ningún tipo de residuos y es efectivo contra organismos patógenos y permite la obtención de alimentos inocuos y sanos. Así lo aseguran quienes han apostado por esta alternativa, cuyo uso ha venido ampliándose en los últimos años. Diversas investigaciones han demostrado que no se producen pérdidas significativas de nutrientes en los alimentos.
Aplicación: detección de explosivos y sustancias peligrosas o prohibidas
Otra aplicación importante aún en fase de I+D es la de la detección de explosivos y sustancias peligrosas o prohibidas mediante la ionización por electrospray, conjuntamente con análisis de movilidad (DMA) y espectrometría de masas (MS / MS). En España, una empresa tecnológica, "SEDET"(Sociedad Europea de Detección), está desarrollando un equipo con estas características útil para la detección de explosivos, drogas o cualquier tipo de sustancias peligrosas o prohibidas que utilizaría la ionización por electrospray. El equipo se denomina "Air Cargo explosivo Screener (ACES)" y está dirigido fundamentalmente a contenedores de carga aérea o puertos.
Sedet es una Joint Venture creada por SEADM, Morpho y CARTIF con el fin de desarrollar esta nueva generación de sistemas de detección de las trazas que dejan las sustancias explosivas.
Un electro-spray (ES) ionizador es un dispositivo que fue propuesto originalmente por Fenn. La mezcla de este aerosol cargado iónicamente con una muestra de aire que pueda contener vapores de explosivos (o partículas) conduce a la ionización de las moléculas de explosivos, ya sea por el contacto con las gotas o por intercambio de carga con los iones producidos por la evaporación de gotas ES. Esto conduce a la formación de iones moleculares que pueden ser analizados en la DMA y la MS. La ionización ES se utiliza con mayor frecuencia para las grandes especies de peso molecular biológicos, pero también es ideal para trazar la detección de explosivos de baja volatilidad por las razones siguientes:
- ESI es una técnica "blanda", es decir, no se fragmenta la molécula a ionizar, permitiendo así que la especificidad y la sensibilidad química mayor.
- ESI permite la ionización de vapores y partículas suspendidas en un gas.
- ESI se pueden adaptar para la ionización de muchos tipos diferentes de moléculas, mezclando un reactivo químico con el líquido pulverizado. El spray crea iones de este reactivo.
La energía de ionización, también llamada potencial de ionización, es la energía que hay que suministrar a un átomo neutro, gaseoso y en estado fundamental, para arrancarle el electrón más débil retenido.
Podemos expresarlo así:
X + 1ªE.I.  X+ + e-
X+ + e-
Siendo esta energía la correspondiente a la primera ionización. La segunda energía de ionización representa la energía necesaria para arrancar un segundo electrón y su valor es siempre mayor que la primera, ya que el volumen de un ión positivo es menor que el del átomo neutro y la fuerza electrostática es mayor en el ión positivo que en el átomo, ya que se conserva la misma carga nuclear:
X+ + 2ªE.I.  X2+ + e-
X2+ + e-
Puedes deducir tú mismo el significado de la tercera energía de ionización y de las posteriores.
La energía de ionización se expresa en electrón-voltio, julios o en Kilojulios por mol (kJ/mol).
1 eV = 1,6.10-19 culombios . 1 voltio = 1,6.10-19 julios
En los elementos de una misma familia o grupo la energía de ionización disminuye a medida que aumenta el número atómico, es decir, de arriba abajo.
En los alcalinos, por ejemplo, el elemento de mayor potencial de ionización es el litio y el de menor el francio. Esto es fácil de explicar, ya que al descender en el grupo el último electrón se sitúa en orbitales cada vez más alejados del núcleo y, además, los electrones de las capas interiores ejercen un efecto de apantallamiento frente a la atracción nuclear sobre los electrones periféricos por lo que resulta más fácil extraerlos.
En los elementos de un mismo período, la energía de ionización crece a medida que aumenta el número atómico, es decir, de izquierda a derecha.
Esto se debe a que el electrón diferenciador está situado en el mismo nivel energético, mientras que la carga del núcleo aumenta, por lo que será mayor la fuerza de atracción y, por otro lado, el número de capas interiores no varía y el efecto de apantallamiento no aumenta.
Sin embargo, el aumento no es continuo, pues en el caso del berilio y el nitrógeno se obtienen valores más altos que lo que podía esperarse por comparación con los otros elementos del mismo período. Este aumento se debe a la estabilidad que presentan las configuraciones s2 y s2p3, respectivamente.
La energía de ionización más elevada corresponde a los gases nobles, ya que su configuración electrónica es la más estable, y por tanto habrá que proporcionar más energía para arrancar un electrón. Puedes deducir y razonar cuáles son los elementos que presentan los valores más elevados para la segunda y tercera energías de ionización.
El método Hückel, propuesto en 1930 por el físico químico alemán Erich Hückel (1896-1980) , es el método de aproximación más simple de la teoría de orbitales moleculares. Su aplicación está restringida al tratamiento de sistemas de hidrocarburos planos con enlaces π conjugados como, por ejemplo, etano (etilo), benceno,butadieno, etc. Sólo es aplicable al estudio de aquellas propiedades que estén dominadas por los orbitales moleculares π. Asimismo, es la base teórica de la regla de Hückel.
Aunque inicialmente sólo trataba sistemas formados en su totalidad por átomos de carbono, más tarde se extendió su uso a otras sustancias como la piridina, el pirrol y el furano, moléculas en cuya composición se encuentran átomos de nitrógeno y oxígeno, entre otros. Son los denominados heteroátomos.
Postulados
El método más simple de la teoría de orbitales moleculares se basa en:
- Existe una separación σ−π, de modo que los orbitales moleculares π están separados del esqueleto σ de la molécula.
- En la construcción de los orbitales moleculares π, sólo intervienen los orbitales p perpendiculares al plano molecular.
- El conjunto de orbitales p constituye una base ortonormal:
 (Donde
(Donde 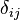 es lDelta de Kronecker)
es lDelta de Kronecker)
- Los elementos de la matriz de Hückel
 se aproximan mediante los parámetros α y β de acuerdo con la siguiente regla:
se aproximan mediante los parámetros α y β de acuerdo con la siguiente regla:
Procedimiento
La aplicación del método Hückel se realiza mediante la construcción del determinante asociado a la molécula, para lo cual es necesario especificar qué átomos la componen y cuál es su conectividad. En un ejemplo sencillo sobre la molécula de etileno (eteno) se tendría:
al que aplicando la regla de determinación de los elementos de la matriz quedaría:
Si se realiza a continuación la sustitución  , pasaría a
, pasaría a 
 , pasaría a
, pasaría a 
Dado que los coeficientes de contribución atómica  no pueden ser nulos, la única opción es que el determinante en los que se incluyen los términos α y β sea nulo:
no pueden ser nulos, la única opción es que el determinante en los que se incluyen los términos α y β sea nulo:
 no pueden ser nulos, la única opción es que el determinante en los que se incluyen los términos α y β sea nulo:
no pueden ser nulos, la única opción es que el determinante en los que se incluyen los términos α y β sea nulo:
Al resolver el determinante se obtiene la energía de los orbitales moleculares π en unidades β (tiene un valor negativo) y los coeficientes  que indican la contribución de un átomo dado r al orbital molecular j.
que indican la contribución de un átomo dado r al orbital molecular j.
 que indican la contribución de un átomo dado r al orbital molecular j.
que indican la contribución de un átomo dado r al orbital molecular j.
Conocidos estos datos se pueden realizar los siguientes cálculos:
- La energía total del sistema π:
- siendo
 el número de electrones en el orbital molecular j y noc el número de orbitales moleculares ocupados.
el número de electrones en el orbital molecular j y noc el número de orbitales moleculares ocupados.
- El orden de enlace π.
El método de Hückel
De los métodos de la Química Cuántica que se aplican al estudio de moléculas orgánicas no saturadas, el de Hückel es el más popular. El éxito de este método se debe a su gran simplicidad, lo que nos permite incluso hacer cálculos a mano, ahora bien, cuando el número de átomos es mayor de tres o cuatro, este cálculo se hace tedioso e impracticable, a menos que la simetría de la molécula permita alguna simplificación; es por ello que se hace necesario el uso del ordenador.Dicho método es aplicable al estudio de las funciones de onda
| (3.1) |
En este método se parte de considerar simplemente:
| (3.2) |
Lógicamente:
| (3.3) |
| (3.4) |
Se consideran los O.M.s
| (3.5) |
En cada
Luego
Aplicando el método variacional de Rayleigh-Ritz, se llega al conjunto de ecuaciones:
| (3.6) |
cuya solución no trivial surge de resolver el determinante secular:
| (3.7) |
Para resolver este determinante, se utilizan las aproximaciones de Hückel:
.
. Si
y
están enlazados
Si
y
no están enlazados
, para todo
.
si
.
Ambos valores ,
Para los heteroátomos se construyen constantes
| (3.8) |
donde
El resultado es un conjunto de orbitales moleculares con sus respectivas energías:
| (3.9) |
Lógicamente, se irán ocupando los de más baja energía, por lo que a cada orbital le corresponderá un número de ocupación (
La energía
| (3.10) |
Energía de deslocalización:
Es la diferencia entre la energía
| (3.11) |
donde
Densidad
La densidad electrónica definida para un O.M. Hückel, será:
| (3.12) |
Y como están normalizados, y las funciones de base son ortonormales,
A partir de esto se puede decir que un electrón definido por un O.M.
| (3.13) |
Siendo
Orden de enlace
Está muy relacionado con lo anterior:
Si tenemos dos átomos
| (3.14) |
nos dará una medida de la densidad electrónica en la región del enlace entre los átomos





No hay comentarios:
Publicar un comentario