Algoritmos cuánticos
algoritmo de Deutsch-Jozsa es un algoritmo cuántico, propuesto por David Deutsch y Richard Jozsa en 1992. Fue uno de los primeros algoritmos diseñados para ejecutar sobre un computador cuántico y que tiene el potencial de ser más eficiente que los algoritmos clásicos al aprovechar el paralelismo inherente de los estados de superposición cuánticos.
En el problema de Deutsch-Jozsa nos dan una función cuántica (que para nosotros es una caja negra) f(x1, x2,..., xn) que toma n bits de entrada x1, x2,..., xn y devuelve un valor binario f(x1, x2,..., xn). Sabemos que la función es constante (0 en todas las entradas o 1 en todas las entradas) o balanceada (devuelve 1 para la mitad de las entradas y 0 para la otra mitad); el problema es entonces determinar cómo es la función (constante o balanceada) aplicando entradas a la caja negra y observando su salida.
Algoritmo de Deutsch
Esta es una versión del algoritmo para una función f(x) de una sola entrada. Se utilizan dos qubits auxiliares en los cálculos. El algoritmo se ilustra en la figura de la derecha.
El bloque H es una puerta Hadamard cuya operación es la siguiente:
El bloque Uf realiza la operación siguiente:
Además,
La entrada al circuito es:  , que atraviesa dos puestas Hardamard (véase la figura) obteniéndose
, que atraviesa dos puestas Hardamard (véase la figura) obteniéndose  . Esto atraviesa el bloque Uf obteneniéndose
. Esto atraviesa el bloque Uf obteneniéndose
 , que atraviesa dos puestas Hardamard (véase la figura) obteniéndose
, que atraviesa dos puestas Hardamard (véase la figura) obteniéndose  . Esto atraviesa el bloque Uf obteneniéndose
. Esto atraviesa el bloque Uf obteneniéndose
Esta expresión puede escribirse:
Al atravesar la última puerta de Hadamard obtenemos:
Puesto que si  y si
y si 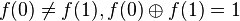 , podemos escribir
, podemos escribir
 y si
y si 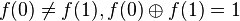 , podemos escribir
, podemos escribir
Este es el resultado final: midiendo el primer qubit de la ecuación obtenemos  . Si resulta el valor 0, entonces la función f(x) es constante, mientras que si resulta 1, la función es balanceada.
. Si resulta el valor 0, entonces la función f(x) es constante, mientras que si resulta 1, la función es balanceada.
 . Si resulta el valor 0, entonces la función f(x) es constante, mientras que si resulta 1, la función es balanceada.
. Si resulta el valor 0, entonces la función f(x) es constante, mientras que si resulta 1, la función es balanceada.Algoritmo de Deutsch-Jozsa
Esta es la versión general del algoritmo para funciones f(x) de n entradas.
En este caso, la entrada al circuito es:
A continuación de las puertas Hadamard se obtiene:
A la salida del bloque Uf se tiene:
La última puerta Hadamard produce la siguiente salida
Y por último, realizando la medición, se obtiene z. En el caso en que la función f(x) sea balanceda, las contribuciones para  se cancelan y la medida de zdebe dar una combinación distinta. Por el contrario, si f(x) es constante se obtiene
se cancelan y la medida de zdebe dar una combinación distinta. Por el contrario, si f(x) es constante se obtiene  en la medida, pues el resto de las contribuciones se cancelan en este caso. Por consiguiente, comprobando si z es cero o distinto de cero se sabe que la función es, respectivamente, constante o balanceada.
en la medida, pues el resto de las contribuciones se cancelan en este caso. Por consiguiente, comprobando si z es cero o distinto de cero se sabe que la función es, respectivamente, constante o balanceada.
 se cancelan y la medida de zdebe dar una combinación distinta. Por el contrario, si f(x) es constante se obtiene
se cancelan y la medida de zdebe dar una combinación distinta. Por el contrario, si f(x) es constante se obtiene  en la medida, pues el resto de las contribuciones se cancelan en este caso. Por consiguiente, comprobando si z es cero o distinto de cero se sabe que la función es, respectivamente, constante o balanceada.
en la medida, pues el resto de las contribuciones se cancelan en este caso. Por consiguiente, comprobando si z es cero o distinto de cero se sabe que la función es, respectivamente, constante o balanceada.
muy buena web , sobre la computación cuántica .- ....................................................:http://www.fisicafundamental.net/misterios/computacion.html
Por razones históricas el primero de los algoritmos a estudiar es el propuesto por David Deutsch en 1985. Aunque en el fondo no sea de una gran utilidad para casos prácticos, en él se empieza a apreciar el funcionamiento y la potencia de los programas cuánticos.
Antes debemos hacer algún comentario sobre la forma de evaluar una función en computación cuántica. Para asegurar la reversibilidad del proceso de evaluación, es necesario siempre un registro auxiliar en donde se guarde el resultado de la consulta auxiliar (a veces denominada query por contagio de los lenguajes de bases de datos) además de encontrarse también los valores iniciales en el registro de salida. Es decir, usaremos un registro dividido en dos, la fuente (source) y el destino (target):
Para implementar una función booleana por tanto necesitaremos únicamente un qubit adicional que nos dé el resultado, el cual se puede evaluar fácilmente mediante la suma módulo 2 (⊕) , o, dicho de otra forma, el operador lógico XOR:
o gráficamente
El problema de Deutsch trata de discernir, para m=1, si la función es constante o no con una sola pregunta. Es decir, una función puede que dé en una query f(0)=1, pero por esto no podemos afirmar, clásicamente, que la función sea constante, habrá que averiguar también cuánto vale f(1), es decir, hacer dos queries. Pues bien, usando adecuadamente el llamado a veces oráculo cuántico Uf (no deja de ser una puerta a la que se le hace una pregunta) se demuestra que con sólo una indagación en computación cuántica podemos averiguar el resultado. El circuito es el siguiente:
Vamos analizar el programa paso por paso. Antes recordemos la forma de actuar del operador de Hadamard:
Partimos del estado inicial
aplicamos los operadores de Hadamard:
ahora haremos actuar el operador que implementa nuestra función, teniendo en cuenta que:
con lo que se podrá poner
y por último el primer qubit pasa por una puerta de Hadamard:
Sólo queda medir el primer qubit. Si está en el estado |0>, la función será constante, de lo contrario no. Esto es así debido al siguiente hecho:
La generalización a funciones booleanas sobre n qubits la hizo Deutsch junto a Richard Jozsa en 1992. Ahora se trataba de ver si una función es constante o está equilibrada o balanceada, es decir, si es 0 para la mitad de las entradas y 1 para el resto. El circuito que se emplea es similar:
Ahora el estado inicial es de la forma:
aplicando los operadores de Hadamard, recordando el resultado en notación decimal se obtiene:
y después de pasar por la puerta funcional queda:
Para aplicar el operador de Hadamard sobre los n primeros estados hay que tener en cuenta el resultado:
por ejemplo
resultado que se puede compactar usando el producto escalar binario pero en notación decimal:
Usando el resultado obtenemos el estado final:
y de nuevo se puede obtener, con una sola medida, que si los primeros n qubits están en el estado |0n> con probabilidad 1, la función será constante, y si la probabilidad es 0, la función estará balanceada, en los restantes casos la función simplemente no sería constante. Como ilustración, los términos para n=2 para el primer qubit serían:
por tanto, con una sola query podemos adivinar la constancia o el balanceo de la función. Nótese que, si a priori sabemos que la función es constante o balanceada, clásicamente en teoría habría que hacer tres medidas para averiguar cuál de las dos opciones es, en el peor de los casos (en el mejor con dos nos valdría). En general en el peor de los casos habría que indagar en la mitad más uno de los posibles resultados, es decir, para una función de n bits habría que hacer 2n/2+1 queries, frente a dos si tenemos suerte o a uno si aplicamos la computación cuántica.
La primera implementación experimental de este algoritmo fue propuesta, para dos qubits, en 1998 por Jonathan Jones y Michele Mosca para técnicas de espines bajo resonancia magnética nuclear (RMN). Hay que señalar que este algoritmo en el fondo no mejora exponencialmente los cálculos clásicos, ya que siempre se puede diseñar un algoritmo clásico probabilista (consultas aleatorias a la función) que nos dé el resultado con gran margen de precisión en muy poco tiempo.
Este algoritmo fue propuesto por Daniel Simon en 1994. Se trata de encontrar el periodo de una función vectorial booleana del tipo:
El periodo por tanto será un vector booleano T que cumpla:
Se puede probar que de nuevo clásicamente habría que evaluar f sobre la mitad más uno de los elementos del dominio (2n-1+1), es decir, el coste sería exponencial. Incluso con un algoritmo probabilista no podríamos ir más acá de las 2n/2 consultas. Veremos que en este caso la ganancia cuántica es clara ya que bastará evaluar Uf unas pocas veces, del orden de n, para encontrar el periodo con una buena cota de aproximación.
Ahora los dos registros del estado inicial tienen n qubits:
Aplicando los operadores de Hadamard al primer registro obtenemos:
Si hacemos actuar ahora la función obtenemos, dado que todos los bits del registro están a cero:
Ahora añadimos un paso que no es necesario pero sí es muy útil desde el punto de vista pedagógico. Se trata de medir el segundo registro y obtener uno de los posibles valores de la función, digamos f(x0), quedando el estado colapsado a:
en donde por supuesto suponemos el estado más general combinación de x0 y x0+T, dado que sólo conocemos el valor de la función. Si ahora aplicamos Hadamard sobre los primeros qubits se obtiene:
en donde lógicamente ahí sólo sobrevivirán los términos que cumplen que T· y=0, ya que el resto interferirá destructivamente. Si ahora medimos el primer registro:
obtendremos para cada estado yi una probabilidad:
Repitiendo estos pasos del orden de n veces obtenemos n vectores yi que nos darán un sistema lineal homogéneo de ecuaciones cuya solución no trivial nos dará las componentes de T:
que podemos resolver con un algoritmo clásico obteniendo T con un orden O(n) de repeticiones. Como se ha dicho, este algoritmo es exponencialmente más eficiente que cualquier algoritmo clásico, incluso de tipo aleatorio.



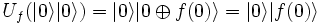
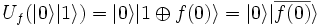













No hay comentarios:
Publicar un comentario