Algoritmos de factorización de enteros
división por tentativa es el algoritmo de factorización de enteros más sencillo y fácil de entender.
Descripción
Dado un entero compuesto n (a lo largo de este artículo, n será «el entero a factorizar»), la división por tentativa consiste en intentar dividir n entre todo número primomenor o igual a √n. Si se encuentra un número que es divisor de n, en división entera, ese número es un factor de n.
Es posible determinar un límite para los factores primos. Supóngase que  es el i-ésimo primo, de modo que
es el i-ésimo primo, de modo que  ,
,  ,
,  etc. Entonces el valor del último número primo probado como un posible factor de n sería
etc. Entonces el valor del último número primo probado como un posible factor de n sería  puesto que
puesto que  ; si fuese igual querría decir que
; si fuese igual querría decir que  es un factor. Aunque todo esto está muy bien, normalmente el inconveniente de inspeccionar un n concreto para determinar el valor correcto de i es más costoso que simplemente probar con el único candidato innecesario
es un factor. Aunque todo esto está muy bien, normalmente el inconveniente de inspeccionar un n concreto para determinar el valor correcto de i es más costoso que simplemente probar con el único candidato innecesario  que estaría incluido en la tentativa con todos los
que estaría incluido en la tentativa con todos los  tales que
tales que  . Puede la raíz cuadrada de n ser entera, entonces es un factor y nes un cuadrado perfecto, pero no es esta una manera buena de encontrarlos.
. Puede la raíz cuadrada de n ser entera, entonces es un factor y nes un cuadrado perfecto, pero no es esta una manera buena de encontrarlos.
 es el i-ésimo primo, de modo que
es el i-ésimo primo, de modo que  ,
,  ,
,  etc. Entonces el valor del último número primo probado como un posible factor de n sería
etc. Entonces el valor del último número primo probado como un posible factor de n sería  puesto que
puesto que  ; si fuese igual querría decir que
; si fuese igual querría decir que  es un factor. Aunque todo esto está muy bien, normalmente el inconveniente de inspeccionar un n concreto para determinar el valor correcto de i es más costoso que simplemente probar con el único candidato innecesario
es un factor. Aunque todo esto está muy bien, normalmente el inconveniente de inspeccionar un n concreto para determinar el valor correcto de i es más costoso que simplemente probar con el único candidato innecesario  que estaría incluido en la tentativa con todos los
que estaría incluido en la tentativa con todos los  tales que
tales que  . Puede la raíz cuadrada de n ser entera, entonces es un factor y nes un cuadrado perfecto, pero no es esta una manera buena de encontrarlos.
. Puede la raíz cuadrada de n ser entera, entonces es un factor y nes un cuadrado perfecto, pero no es esta una manera buena de encontrarlos.
La división por tentativa garantiza encontrar un factor de n, puesto que comprueba todos los factores primos posibles de n. Por tanto, si el algoritmo no encuentra ningún factor, es una prueba de que n es primo.
Complejidad computacional
En el peor caso, la división por tentativa es un algoritmo costoso. Si se empieza en 2 y se va subiendo hasta la raíz cuadrada de n, el algoritmo requiere
tentativas, donde  es la función contador de primos, el número de primos menores que x. En lo anterior no se ha tenido en cuenta la sobrecarga del test de primalidad para obtener los números primos candidatos a ser factores. Si se utiliza una variante sin el test de primalidad, sencillamente dividiendo por todo número impar menor que la raíz cuadrada de n, ya sea primo o no, puede llegar a necesitarse alrededor de
es la función contador de primos, el número de primos menores que x. En lo anterior no se ha tenido en cuenta la sobrecarga del test de primalidad para obtener los números primos candidatos a ser factores. Si se utiliza una variante sin el test de primalidad, sencillamente dividiendo por todo número impar menor que la raíz cuadrada de n, ya sea primo o no, puede llegar a necesitarse alrededor de
 es la función contador de primos, el número de primos menores que x. En lo anterior no se ha tenido en cuenta la sobrecarga del test de primalidad para obtener los números primos candidatos a ser factores. Si se utiliza una variante sin el test de primalidad, sencillamente dividiendo por todo número impar menor que la raíz cuadrada de n, ya sea primo o no, puede llegar a necesitarse alrededor de
es la función contador de primos, el número de primos menores que x. En lo anterior no se ha tenido en cuenta la sobrecarga del test de primalidad para obtener los números primos candidatos a ser factores. Si se utiliza una variante sin el test de primalidad, sencillamente dividiendo por todo número impar menor que la raíz cuadrada de n, ya sea primo o no, puede llegar a necesitarse alrededor de
tentativas, que para un n grande es peor.
Esto significa que para un n con factores primos grandes de tamaños similares (como aquellos empleados en la criptografía asimétrica), la división por tentativa es computacionalmente impracticable.
Sin embargo, para un n con al menos un factor pequeño, la división por tentativa puede ser un método rápido para encontrar ese factor pequeño. Vale la pena percatarse de que para un n aleatorio, existe un 50% de probabilidad de que 2 sea un factor de n, un 33% de probabilidad de que 3 sea un factor, y así sucesivamente. Se puede observar que el 88% de todos los enteros positivos tiene un factor menor que 100, y que el 91% tiene un factor menor que 1000.
LA CRIBA DE ERASTÓTENES y DIVISIÓN POR TENTATIVA
Las pruebas rápidas de primalidad son utilizados para la determinación de primos pequeños. Son procesos manuales que, obviamente, también pueden ser realizados por el ordenador. Sus algoritmos son simples sin embargo no necesariamente rápidos, tanto es que, en determinadas situaciones, los procedimientos manuales son más rápidos que los informatizados.
Lo CRIBO DE ERATÓSTENES
Para encontrar todos los números primos en una lista de números enteros pequeños, el modo más rápido y fácil es lo de Erastótenes. Teniendo en cuenta que la multiplicación es una operación más fácil de realizar que la división, Erastótenes de Cirene (el siglo III a.C.) tuvo la brillante idea de organizar estas computaciones en forma de criba o tamiz.
Creando uno cribo
Uno de los medios más eficientes de hallar todos los números primos pequeños, por ejemplo los menores que 10.000.000, es usando la Criba de Erastótenes (± 240 a.C.). Basta hacer una lista con todos los enteros mayores que uno y menores o igual a n y tachar los múltiplos de todos los primos menores o igual a la raíz cuadrada de n (n½). Los números que no estuvieran tachados son los números primos.
Vamos a determinar, por ejemplo, los primos menores o igual la 20:
1. Inicialmente se hace la lista de los enteros de 2 la 20.
| 2. | 3. | 4. | 5. | 6. | 7. | 8. | 9. | 10. | |
| 11. | 12. | 13. | 14. | 15. | 16. | 17. | 18. | 19. | 20. |
2. El primer número (2) es primo. Vamos a mantenerlo y tachar todos sus múltiplos. De esta forma, obtenemos:
| 2. | 3. | 5. | 7. | 9. | |||||
| 11. | 13. | 15. | 17. | 19. |
3. El próximo número "libre" es el 3, otro primo. Vamos a mantenerlo y tachar sus múltiplos:
| 2. | 3. | 5. | 7. | ||||||
| 11. | 13. | 17. | 19. |
4. El próximo número primo es 5, sin embargo no es necesario repetir el procedimiento porque 5 es mayor que la raíz cuadrada de 20 (20½ = 4,4721). Los números restantes son primos, destacados abajo:
| 2. | 3. | 5. | 7. | ||||||
| 11. | 13. | 17. | 19. |
Los números primos encontrados fueron {2, 3, 5, 7, 11, 13, 17, 19}.
La DIVISIÓN POR TENTATIVA
Para determinar si un determinado número entero pequeño es primo, la división por tentativa funciona bien. Basta dividirlo por todos los primos menores o igual a la su raíz cuadrada.
Por ejemplo, queremos saber se 323 es un número primo. La raíz cuadrada de 323 es 323½ = 17,9722, por lo tanto, vamos a dividir 323 por 2, 3, 5, 7, 11 y 17. Si ninguno de estos primos dividir 323, entonces él será primo:
| División | Resto | Divide |
| 323 ÷ 2 = 161. | 1. | No |
| 323 ÷ 3 = 107. | 2. | No |
| 323 ÷ 5 = 64. | 3. | No |
| 323 ÷ 7 = 46. | 1. | No |
| 323 ÷ 11 = 29. | 4. | No |
| 323 ÷ 13 = 24. | 11. | No |
| 323 ÷ 17 = 19. | 0. | SÍ |
El entero 323 NO es primo porque es dividido por 17.
Si estuviéramos buscando por un primo titânico, con más de 10.000 dígitos decimales, nunca podríamos dividirlo por todos los primos menores que su raíz cuadrada. Aun así, aún en estos casos la división por tentativa es utilizada, solamente para hacer un rastreo inicial. Se hace divisiones por algunos millones de primos pequeños y después se aplica una prueba de primalidad.
En el caso de que n haya 25 dígitos o más, la división por tentativa usando primos menores que su raíz cuadrada es impracticable. Si n tuviera 200 dígitos, entonces la división por tentativa es imposible.
la factorización con fracciones continuas, conocido como método de factorización con fracciones continuas(CFRAC del inglés Continued Fraction Factorization Method ) es un algoritmo de factorización de enteros. Es un algoritmo de propósito general, lo que significa que es apropiado para factorizar cualquier entero n, no dependiente de una forma espacial o de propiedades. Fue descrito por D. H. Lehmer y R. E. Powers en 1931,1 y desarrollado como un algoritmo de computadora por Michael A. Morrison yJohn Brillhart en 1975.2
El método de fracciones continuas está basado sobre el método de factorización de Dixon. Este usa convergentes en las expansiones de fracciones continuas regulares de
 .
.
Puesto que es un irracional cuadrático, la fracción continua debe de ser periódica (a no ser que n sea un cuadrado, en cuyo caso la factorización es obvia).
La factorización de curva elíptica de Lenstra o método de factorización de curva elíptica ( del inglés elliptic curve factorization method, ECM) es un rápido algoritmo de tiempo de ejecución sub-exponencial para la factorización de enteros que emplea curvas elípticas. Para una factorización de propósito general, ECM es el tercer método más rápido conocido de factorización. El segundo más rápido es la criba cuadrática de múltiples polinomios y el más rápido es la criba general del cuerpo de números. La factorización de curva elíptica de Lenstra es llamada así en honor a Hendrik Lenstra.
Prácticamente hablando, ECM es considerado un algoritmo de factorización de propósito especial así como el más adecuado para encontrar factores pequeños. A fecha de 2012, es todavía el mejor algoritmo para divisores que no superen los 20 a 25 dígitos decimales(64 a 83 bits respectivamente), así como su tiempo de ejecución está dominado por el tamaño del factor más pequeño p en lugar de por el tamaño del número n a ser factorizado. Frecuentemente, ECM se usa para eliminar factores pequeños de un entero muy grande con muchos factores; si el entero resultante todavía es compuesto, entonces solo tiene factores grandes y es factorizado mediante el uso de técnicas de propósito general. El factor más grande encontrado usando ECM cuenta con 75 dígitos y fue descubierto el 2 de agosto de 2012 por Samuel Wagstaff.1 Incrementando el número de curvas probadas se mejoran las posibilidades de encontrar un factor, pero no son lineales con el incremento en el número de dígitos.
La factorización de formas cuadradas de Shanks es un método para factorizar enteros inventado por Daniel Shanks como una mejora del método de factorización de Fermat.
El éxito del método de depende de encontrar números enteros  e
e  tales que
tales que  , donde
, donde  es el entero a ser factorizado. Una mejora (indicada por Kraitchik) es buscar enteros
es el entero a ser factorizado. Una mejora (indicada por Kraitchik) es buscar enteros  e
e  tales que
tales que  . Encontrando un par adecuado
. Encontrando un par adecuado  no se garantiza una factorización de
no se garantiza una factorización de  , pero esto implica que
, pero esto implica que  es un factor de
es un factor de 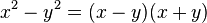 , y hay una buena posibilidad de que los divisores primos de
, y hay una buena posibilidad de que los divisores primos de  estén distribuidos entre esos dos factores, así que el cálculo del máximo común divisor de
estén distribuidos entre esos dos factores, así que el cálculo del máximo común divisor de  y
y  dará un factor no trivial de
dará un factor no trivial de  .
.
 e
e  tales que
tales que  , donde
, donde  es el entero a ser factorizado. Una mejora (indicada por Kraitchik) es buscar enteros
es el entero a ser factorizado. Una mejora (indicada por Kraitchik) es buscar enteros  e
e  tales que
tales que  . Encontrando un par adecuado
. Encontrando un par adecuado  no se garantiza una factorización de
no se garantiza una factorización de  , pero esto implica que
, pero esto implica que  es un factor de
es un factor de 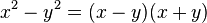 , y hay una buena posibilidad de que los divisores primos de
, y hay una buena posibilidad de que los divisores primos de  estén distribuidos entre esos dos factores, así que el cálculo del máximo común divisor de
estén distribuidos entre esos dos factores, así que el cálculo del máximo común divisor de  y
y  dará un factor no trivial de
dará un factor no trivial de  .
.
Una algoritmo práctico para encontrar pares  que satisfagan
que satisfagan  fue desarrollado por Shanks, que lo llamóFactorización de formas cuadradas (en inglés Square Forms Factorization o SQUFOF). El algoritmo puede ser expresado en términos defracciones continuas, o en términos de formas cuadráticas.A pesar de que ahora existen métodos de factorización más eficientes disponibles, SQUFOF tiene la ventaja de que es lo suficientemente pequeño para ser implementado en una calculadora programable.
fue desarrollado por Shanks, que lo llamóFactorización de formas cuadradas (en inglés Square Forms Factorization o SQUFOF). El algoritmo puede ser expresado en términos defracciones continuas, o en términos de formas cuadráticas.A pesar de que ahora existen métodos de factorización más eficientes disponibles, SQUFOF tiene la ventaja de que es lo suficientemente pequeño para ser implementado en una calculadora programable.
 que satisfagan
que satisfagan  fue desarrollado por Shanks, que lo llamóFactorización de formas cuadradas (en inglés Square Forms Factorization o SQUFOF). El algoritmo puede ser expresado en términos defracciones continuas, o en términos de formas cuadráticas.A pesar de que ahora existen métodos de factorización más eficientes disponibles, SQUFOF tiene la ventaja de que es lo suficientemente pequeño para ser implementado en una calculadora programable.
fue desarrollado por Shanks, que lo llamóFactorización de formas cuadradas (en inglés Square Forms Factorization o SQUFOF). El algoritmo puede ser expresado en términos defracciones continuas, o en términos de formas cuadráticas.A pesar de que ahora existen métodos de factorización más eficientes disponibles, SQUFOF tiene la ventaja de que es lo suficientemente pequeño para ser implementado en una calculadora programable.

![O\left(e^{\sqrt{2\log n \log\log n}}\right)=L_n\left[1/2,\sqrt{2}\right]](https://upload.wikimedia.org/math/5/3/7/53775a79d6335c647e21011c569b5b02.png) , en las notaciones
, en las notaciones
No hay comentarios:
Publicar un comentario