Algoritmos cuánticos
transformada cuántica de Fourier es una transformación sobre bits cuánticos, y es la analogía cuántica de la transformada de Fourier discreta. La transformada de Fourier es una parte de muchos algoritmos cuánticos, el algoritmo de factorización de Shor y el cálculo del logaritmo discreto, el algoritmo de estimación de fase para estimar los eigenvalores de un operador unitario, y logaritmos para HSP hidden subgroup problem.
La transformada de Fourier puede ser realizada eficientemente en un ordenador cuántico, con una particular descomposición en un producto de matrices unitarias simples. Usando una descomposición simple, la trasformación discreta de Fourier puede ser implementada como un circuito cuántico que tiene solo  puertas Hadamar y puertas de desplazamiento de fase controladas, donde
puertas Hadamar y puertas de desplazamiento de fase controladas, donde  es el número de qubits.1 Esto puede ser comparado con la transformada de Fourier discreta, que utiliza
es el número de qubits.1 Esto puede ser comparado con la transformada de Fourier discreta, que utiliza  puertas (donde
puertas (donde  es el número de bits), lo cual es exponencialmente mejor que
es el número de bits), lo cual es exponencialmente mejor que  . Sin embargo, la transformada cuántica de Fourier actúa sobre un estado cuántico, mientras que la trasformada de Fourier clásica actúa sobre un vector, así que no todas las tareas que usan la transformada de Fourier clásica pueden utilizar la ventaja de esta aceleración exponencial.
. Sin embargo, la transformada cuántica de Fourier actúa sobre un estado cuántico, mientras que la trasformada de Fourier clásica actúa sobre un vector, así que no todas las tareas que usan la transformada de Fourier clásica pueden utilizar la ventaja de esta aceleración exponencial.
 puertas Hadamar y puertas de desplazamiento de fase controladas, donde
puertas Hadamar y puertas de desplazamiento de fase controladas, donde  es el número de qubits.1 Esto puede ser comparado con la transformada de Fourier discreta, que utiliza
es el número de qubits.1 Esto puede ser comparado con la transformada de Fourier discreta, que utiliza  puertas (donde
puertas (donde  es el número de bits), lo cual es exponencialmente mejor que
es el número de bits), lo cual es exponencialmente mejor que  . Sin embargo, la transformada cuántica de Fourier actúa sobre un estado cuántico, mientras que la trasformada de Fourier clásica actúa sobre un vector, así que no todas las tareas que usan la transformada de Fourier clásica pueden utilizar la ventaja de esta aceleración exponencial.
. Sin embargo, la transformada cuántica de Fourier actúa sobre un estado cuántico, mientras que la trasformada de Fourier clásica actúa sobre un vector, así que no todas las tareas que usan la transformada de Fourier clásica pueden utilizar la ventaja de esta aceleración exponencial.
Los mejores algoritmos cuánticos de transformada de Fourier conocidos actualmente requieren solo  puertas para alcanzar una aproximación eficiente.
puertas para alcanzar una aproximación eficiente.
 puertas para alcanzar una aproximación eficiente.
puertas para alcanzar una aproximación eficiente.Definición
La transformada de Fourier cuántica es la transformada de Fourier discreta clásica aplicada al vector de amplitudes de un estado cuántico. La transformada de Fourier clásica (unitaria) actúa sobre un vector en 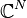 , (x0,..., xN−1) y lo mapea al vector (y0,..., yN−1) de acuerdo con la fórmula:
, (x0,..., xN−1) y lo mapea al vector (y0,..., yN−1) de acuerdo con la fórmula:
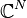 , (x0,..., xN−1) y lo mapea al vector (y0,..., yN−1) de acuerdo con la fórmula:
, (x0,..., xN−1) y lo mapea al vector (y0,..., yN−1) de acuerdo con la fórmula:
Donde  es una raíz de la unidad Nth primitiva.
es una raíz de la unidad Nth primitiva.
 es una raíz de la unidad Nth primitiva.
es una raíz de la unidad Nth primitiva.
De forma similar, la transformada cuántica de Fourier actúa sobre un estado cuántico  y lo mapea a un estado cuántico
y lo mapea a un estado cuántico  de acuerdo con la fórmula:
de acuerdo con la fórmula:
 y lo mapea a un estado cuántico
y lo mapea a un estado cuántico  de acuerdo con la fórmula:
de acuerdo con la fórmula:
Esto puede ser expresado como la aplicación
De forma equivalente, la transformada de Fourier cuántica puede ser vista como una matriz unitaria actuando sobre vectores estado cuántico, donde la matriz unitaria 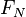 está dada por
está dada por
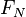 está dada por
está dada porPropiedades
Unitaria
Muchas de las propiedades de la transformada de Fourier surgen del hecho de que es una transformación unitaria. Esto puede ser comprobado realizando la multiplicación de matrices y verificando la relación  , donde
, donde  es la Hermitica adjunta de
es la Hermitica adjunta de  . Alternativamente, podemos comprobar que los vectores de norm 1 obtienen relación con los vectores de 1.
. Alternativamente, podemos comprobar que los vectores de norm 1 obtienen relación con los vectores de 1.
 , donde
, donde  es la Hermitica adjunta de
es la Hermitica adjunta de  . Alternativamente, podemos comprobar que los vectores de norm 1 obtienen relación con los vectores de 1.
. Alternativamente, podemos comprobar que los vectores de norm 1 obtienen relación con los vectores de 1.
De las propiedades unitarias surge que la inversa de la transformada cuántica de Fourier es la hermítica adjunta de la matriz de Fourier, así  . Existe un circuito cuántico eficiente que implementa la transformada inversa cuántica de Fourier. Así que ambas transformaciones pueden ser realizadas en un ordenador cuántico.
. Existe un circuito cuántico eficiente que implementa la transformada inversa cuántica de Fourier. Así que ambas transformaciones pueden ser realizadas en un ordenador cuántico.
 . Existe un circuito cuántico eficiente que implementa la transformada inversa cuántica de Fourier. Así que ambas transformaciones pueden ser realizadas en un ordenador cuántico.
. Existe un circuito cuántico eficiente que implementa la transformada inversa cuántica de Fourier. Así que ambas transformaciones pueden ser realizadas en un ordenador cuántico.Implementación del Circuito
La transformada de Fourier puede ser implementada aproximadamente para cualquier N, sin embargo, la implementación para el caso en el que N es una potencia de 2 es mucho más simple. Supongamos N = 2n. Tenemos la base ortogonal consistente en los vectores
La base de todos los posibles estados de los qubits es:
donde, con la notación producto tensorial  ,
,  indica que el qubit
indica que el qubit  está en el estado
está en el estado  , con
, con  entre 0 y 1. Por convención, el índice de la base de estados
entre 0 y 1. Por convención, el índice de la base de estados  ordena los posibles estados de los qubits lexicográficamente, por ejemplo, por convención el paso de binario a decimal es de la forma.:
ordena los posibles estados de los qubits lexicográficamente, por ejemplo, por convención el paso de binario a decimal es de la forma.:
 ,
,  indica que el qubit
indica que el qubit  está en el estado
está en el estado  , con
, con  entre 0 y 1. Por convención, el índice de la base de estados
entre 0 y 1. Por convención, el índice de la base de estados  ordena los posibles estados de los qubits lexicográficamente, por ejemplo, por convención el paso de binario a decimal es de la forma.:
ordena los posibles estados de los qubits lexicográficamente, por ejemplo, por convención el paso de binario a decimal es de la forma.:
Esto también es útil para la notación binaria fraccionaria:
Por tanto, ![[0.x_1] = \frac{x_1}{2}](https://upload.wikimedia.org/math/8/1/f/81f5aa000c6e06bb4c4f7d3754163847.png) and
and ![[0.x_1 x_2] = \frac{x_1}{2}+\frac{x_2}{2^2}.](https://upload.wikimedia.org/math/9/2/3/92321535d9bde231974bcc49dd9a44b5.png)
![[0.x_1] = \frac{x_1}{2}](https://upload.wikimedia.org/math/8/1/f/81f5aa000c6e06bb4c4f7d3754163847.png) and
and ![[0.x_1 x_2] = \frac{x_1}{2}+\frac{x_2}{2^2}.](https://upload.wikimedia.org/math/9/2/3/92321535d9bde231974bcc49dd9a44b5.png)
Con esta notación, la acción de la transformada de Fourier cuántica puede ser expresada por:
donde la salida del qubit 1 es una superposición del estado 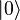 y
y ![e^{2 \pi i \, [0.x_n] }|1\rangle](https://upload.wikimedia.org/math/e/3/0/e30cfa739a36e5f6814be428c34e1f19.png) , y así en los otros qubits.
, y así en los otros qubits.
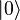 y
y ![e^{2 \pi i \, [0.x_n] }|1\rangle](https://upload.wikimedia.org/math/e/3/0/e30cfa739a36e5f6814be428c34e1f19.png) , y así en los otros qubits.
, y así en los otros qubits.
En otras palabras, la operación de la transformada de Fourier discreta sobre n-qubits, puede ser factorizada dentro del producto tensor de n qubits-únicos, sugiriendo que es fácil de representar en un circuito cuántico. De hecho, cada una de las operaciones de los qubits-únicos puede ser implementada eficientemente usando una puerta Hadamar y puertas controladas de desplazamiento de fase. El primer término requiere una puerta Hadamar, el siguiente requiere una puerta Hadamar y una puerta controlada de desplazamiento de fase y cada siguiente término requiere una puerta adicional de desplazamiento de fase. Sumando el número de puertas da  puertas, el cual es proporcional al número de qubits.
puertas, el cual es proporcional al número de qubits.
 puertas, el cual es proporcional al número de qubits.
puertas, el cual es proporcional al número de qubits.Ejemplo
Considerar la transformada cuántica de Fourier sobre 3 qubits. Es la siguiente transformación:
donde  satisface
satisface  (ya que
(ya que  ).
).
 satisface
satisface  (ya que
(ya que  ).
).
La matriz que representa esta transformación es
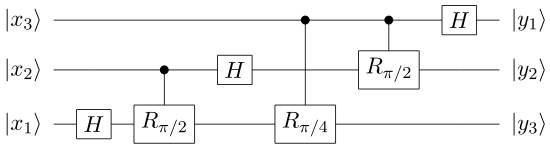
La transformada de Fourier cuántica de 3-qubit es las siguiente operación:
Este circuito cuántico implementa la transformada cuántica de Fourier sobre el estado cuántico  .
.
 .
.
Las puertas cuánticas usadas en el circuito de arriba son la puerta Hadamar y la puerta controlada de desplazamiento de fase  .
.
 .
.
Como se calculó antes, el número de puertas usadas es  lo cual es igual a 6, para n = 3.
lo cual es igual a 6, para n = 3.
 lo cual es igual a 6, para n = 3.
lo cual es igual a 6, para n = 3.La Transformada de Fourier Cuántica (QFT)
La transformada de Fourier cuántica toma un estado  y lo transforma en un estado
y lo transforma en un estado  tal que
tal que
donde los  son los coeficientes de la transformada de Fourier de
son los coeficientes de la transformada de Fourier de  . Como los estados cuánticos deben estar normalizados, la transformada de Fourier cuántica cumple con la siguiente ecuación
. Como los estados cuánticos deben estar normalizados, la transformada de Fourier cuántica cumple con la siguiente ecuación
Si el estado cuántico además corresponde a una secuencia de qubits podemos decir que  y la expresión se traduce a
y la expresión se traduce a
También sabemos que el coeficiente  multiplica al ket base
multiplica al ket base  asi que
asi que
Y como  es el coeficiente del vector base
es el coeficiente del vector base  , entonces por linealidad la ecuación 3.5 es equivalente a decir que
, entonces por linealidad la ecuación 3.5 es equivalente a decir que
ya que
El algoritmo del temple cuántico (en inglés, quantum annealing), también llamado aleación, cristalización o recocido, es análogo al temple simulado pero sustituyendo la activación térmica por el efecto túnel.
QA es una clase algorítmica parecida al temple simulado (“Simulated Annealing” o 'SA' de Kirkpatrick y otros) que consiste en una adaptación del algoritmo clásico deMetropolis-Hastings. Sin embargo, QA emplea un campo cuántico en lugar de ungradiente térmico. Para explorar el paisaje del problema de optimización, SA y sus variantes (como el Temple Paralelo) aprovechan las fluctuaciones “térmicas” correspondientes a gradientes de temperatura, mientras que QA utiliza para ello fluctuaciones “cuánticas”. Una fluctuación cuántica es un cambio en la cantidad de energía de un punto del espacio durante brevísimos lapsos de tiempo, como resultado del principio de incertidumbre enunciado por Heisemberg.
En cierto modo, los métodos de temple, cristalización o 'annealing' son una metáfora de la naturaleza que trata de imitar la forma en que se ordenan las moléculas de un metal al magnetizarse, o de un cristal durante la transición de fase, que ocurre por ejemplo, al enfriarse el agua o el dióxido de silicio tras haber sido previamente calentados: si el enfriamiento fuese lento, habitualmente el cristal así generado tendrá pocas imperfecciones (es decir, se encontrará en un metaestado de baja energía) que si se enfriara demasiado rápido (metaestado de alta energía). Este modelo físico natural se basa en la propensión a minimizar su energía libre (en el sentido de Helmholtz) de un sistema ergódico, tal como un sistema termodinámico cerrado en que todos los estados configuracionales sean equiprobables.
Los métodos de temple se basan por lo general en el algoritmo de Monte Carlo, que repite una gran cantidad de muestreos aleatorios sobre un hipercubo de dimensión 'N' (espacio de soluciones del problema), a fin de generar estados muestrales y permitiendo reducir mucho la complejidad de cómputo a costa de perder algo de precisión estadística.
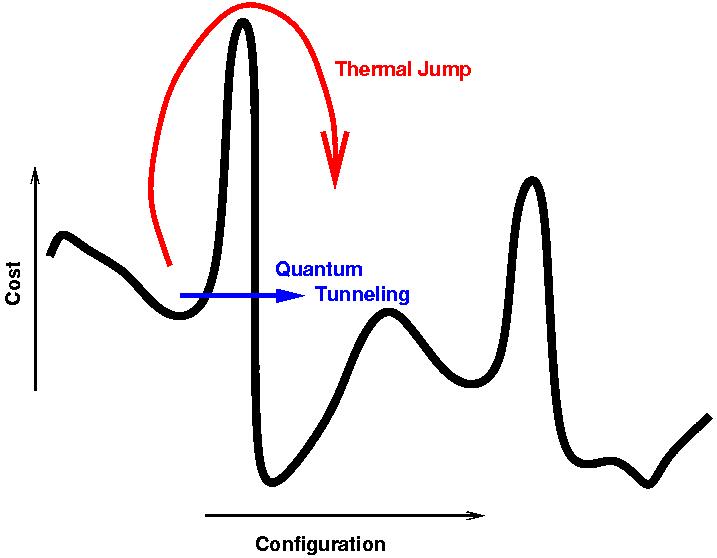








![[0. x_1 \ldots x_m] = \sum_{k = 1}^m x_k 2^{-k}.](https://upload.wikimedia.org/math/9/c/d/9cd5c7ee8df1996a331263e2b02bc537.png)
![|x_1 x_2 \ldots x_n \rangle \mapsto \frac{1}{\sqrt{N}} \ \left(|0\rangle + e^{2 \pi i \, [0.x_n] }|1\rangle\right) \otimes \left(|0\rangle + e^{2 \pi i \, [0.x_{n-1} x_n] }|1\rangle\right) \otimes \cdots \otimes \left(|0\rangle + e^{2 \pi i \, [0.x_1 x_2 \ldots x_n] }|1\rangle\right),](https://upload.wikimedia.org/math/1/5/4/15453e44e07cfbe599333ba53040a2a2.png)


![|x_1, x_2, x_3 \rangle \mapsto \frac{1}{\sqrt{2^3}} \ \left(|0\rangle + e^{2 \pi i \, [0.x_3] }|1\rangle\right) \otimes \left(|0\rangle + e^{2 \pi i \, [0.x_2 x_3] }|1\rangle\right) \otimes \left(|0\rangle + e^{2 \pi i \, [0.x_1 x_2 x_3] }|1\rangle\right).](https://upload.wikimedia.org/math/2/6/0/260889278fdba569f7120592610bf843.png)
No hay comentarios:
Publicar un comentario