Algoritmos de precisión arbitraria
El algoritmo de Toom-Cook, a veces conocido como Toom-3, nombrado así por los autores Andrei Toom y Stephen Cook, es unalgoritmo de multiplicación, un método para multiplicar dos números enteros que son muy grandes.
Dados 2 números enteros, a y b, Toom-Cook divide los números a y b en k partes más pequeñas, todas de longitud l, y realiza las operaciones sobre las partes, Conforme la k va creciendo va combinando muchas de las suboperaciones de multiplicación, reduciendo así poco a poco la complejidad total del algoritmo. Las suboperaciones de multiplicación ahora sí se pueden realizar recursivamente usando de nuevo el método de multiplicación Toom-Cook, y así sucesivamente. Aunque los términos "Toom-3" y "Toom-Cook" se utilizan a veces incorrectamente como sinónimos, Toom-3 es una única instancia del algoritmo de Toom-Cook, donde k = 3.
la aproximación de Spouge es una fórmula para la función gamma expresada por John L. Spouge en 1994.1 Es una modificación de la aproximación de Stirling, y tiene la forma
donde una es un número entero positivo arbitrario y los coeficientes vienen dados por
Spouge demostró que, si Re (z)> 0 y una> 2, el error relativo en descartar ε un (z) está delimitada por
La fórmula es similar a la aproximación de Lanczos, pero tiene algunas características distintas. Respecto a la fórmula de Lanczos exhibe una convergencia más rápida, los coeficientes son mucho más fáciles de calcular y el error se pueden establecer arbitrariamente baja. La fórmula es, por tanto, factible para evaluar la función gamma con precisión arbitraria. Sin embargo, se debe tener especial atención para utilizar la suficiente precisión al calcular la suma debido al gran tamaño de los coeficientes CK, así como su signo alternante. Por ejemplo, para un = 49, debe calcular la suma utilizando aproximadamente 65 dígitos decimales de precisión con el fin de obtener los prometidos 40 dígitos decimales de precisión.
Iguales en gama de colores negra:
El dominio de la función gamma es el half-line verdadero positivo y half-line negativo con números enteros cero y negativos excluidos. El rango de la función gamma es línea verdadera entera. Como una función gamma de la función compleja tiene infinito del valor (tiene un poste) en el número entero no positivo x.
Observando dimensión de una variable general de la función gamma podemos decir que los métodos numéricos de la aproximación tendrán exactitud muy buena en los intervalos (0.5, 3), y acercar - n+0.5, especialmente para la exactitud grande del N. será bueno para la exactitud de x>2. estará bajo cerca de los números enteros negativos, especialmente alrededor 0, -1, -2.
exponenciación binaria es un algoritmo utilizado para calcular de forma rápida grandes potencias enteras de un número
 dado. También es conocido comopotenciación por cuadrados o elevar al cuadrado y multiplicar. Implícitamente utiliza la expansión binaria del exponente. Es de uso bastante regular en aritmética modular. Este algoritmo es similar al de la duplicación en la multiplicación.
dado. También es conocido comopotenciación por cuadrados o elevar al cuadrado y multiplicar. Implícitamente utiliza la expansión binaria del exponente. Es de uso bastante regular en aritmética modular. Este algoritmo es similar al de la duplicación en la multiplicación.Versión recurrente
Fundamentos
El algoritmo está basado en las siguientes tres propiedades de la potencia:
(1)
(2)
(3)
Usando  y
y 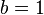 en la ecuación () se sigue que
en la ecuación () se sigue que  . Tomando
. Tomando  y
y 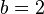 en la ecuación () se obtiene que
en la ecuación () se obtiene que  .
.
 y
y 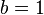 en la ecuación () se sigue que
en la ecuación () se sigue que  . Tomando
. Tomando  y
y 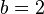 en la ecuación () se obtiene que
en la ecuación () se obtiene que  .
.Algoritmo
Comparado con el método original de multiplicar  por sí mismo
por sí mismo  veces, este algoritmo sólo utiliza O(log n) multiplicaciones y acelera el cálculo de
veces, este algoritmo sólo utiliza O(log n) multiplicaciones y acelera el cálculo de  tremendamente; más o menos de la misma forma que el algoritmo de la multiplicación acelera una multiplicación sobre el método más lento de realizar una suma repetida.
tremendamente; más o menos de la misma forma que el algoritmo de la multiplicación acelera una multiplicación sobre el método más lento de realizar una suma repetida.
 por sí mismo
por sí mismo  veces, este algoritmo sólo utiliza O(log n) multiplicaciones y acelera el cálculo de
veces, este algoritmo sólo utiliza O(log n) multiplicaciones y acelera el cálculo de  tremendamente; más o menos de la misma forma que el algoritmo de la multiplicación acelera una multiplicación sobre el método más lento de realizar una suma repetida.
tremendamente; más o menos de la misma forma que el algoritmo de la multiplicación acelera una multiplicación sobre el método más lento de realizar una suma repetida.Aplicaciones
La misma idea permite el cálculo rápido de potencias muy grandes en módulo. Especialmente en criptografía, es útil calcular potencias en el anillo de los enteros módulo q.
La idea puede ser usada también para computar potencias de números enteros en un semigrupo, usando la regla
- Potencia(x, -n) = (Potencia(x, n))-1.
Este método funciona en cualquier semigrupo, y es usado frecuentemente para calcular potencias de matrices.
Por ejemplo, la evaluación de
- 13789722341 (mod 2345)
tomaría mucho tiempo y espacio de almacenamiento si el método ingenuo es usado: calcular 13789722341 y tomar el residuio cuando es dividido por 2345. Incluso usando un método más efectivo tomará tiempo considerable: elevar 13789 al cuadrado , tomar el residuo cuando se divide por 2345, multiplicar el resultado por 13789, y así sucesivamente. Este proceso realizará 722340 multplicaciones modulares. Este algoritmo está basado en la observación que 13789722341 = 13789(137892)361170. Entonces, si se calcula 137892, el cálculo completo tomaría 361170 multiplicaciones modulares. Ésta es una ganacia en un factor de dos. Pero como el nuevo problema sigue siendo similar al anterior, se puede aplicar la observación nuevamente, reduciendo a la mitad la cantidad, aproximadamente.
La aplicación sucesiva de este algoritmo es equivalente a descomponer el exponente (convirtiéndolo a base binaria) en una secuencia de cuadrados y multiplicaciones: por ejemplo
- x13 = x1101bin
- = x(1*2^3 + 1*2^2 + 0*2^1 + 1*2^0)
- = x1*2^3 * x1*2^2 * x0*2^1 * x1*2^0
- = x2^3 * x2^2 * 1 * x2^0
- = x8 * x4 * x1
- = (x4)2 * (x2)2 * x
- = (x4 * x2)2 * x
- = ((x2)2 * x2)2 * x
- = ((x2 * x)2)2 * x → algoritmo necesita sólo 5 multiplicaciones en vez de 13 - 1 = 12
Algunos ejemplos más:
- x10 = ((x2)2*x)2 porque 10 = (1,010)2 = 23+21, algoritmo necesita 4 multiplicaciones en vez de 9
- x100 = (((((x2*x)2)2)2*x)2)2 porque 100 = (1,100,100)2 = 26+25+22, algoritmo necesita 8 multiplicaciones en vez de 99
- x1,000 = ((((((((x2*x)2*x)2*x)2*x)2)2*x)2)2)2 porque 103 = (1,111,101,000)2, algoritmo necesita 14 multiplicaciones en vez de 999
- x1,000,000 = ((((((((((((((((((x2*x)2*x)2*x)2)2*x)2)2)2)2)2*x)2)2)2*x)2)2)2)2)2)2 porque 106 = (11,110,100,001,001,000,000)2, algoritmo necesita 25 multiplicaciones
- x1,000,000,000 = ((((((((((((((((((((((((((((x2*x)2*x)2)2*x)2*x)2*x)2)2)2*x)2*x)2)2*x)2)2*x)2*x)2)2)2*x)2)2*x)2)2)2)2)2)2)2)2)2 porque 109 = (111,011,100,110,101,100,101,000,000,000)2, algoritmo necesita 41 multiplicaciones
![\Gamma(z+1) = (z+a)^{z+1/2} e^{-(z+a)} \left[ c_0 + \sum_{k=1}^{a-1} \frac{c_k}{z+k} + \varepsilon_a(z) \right]](https://upload.wikimedia.org/math/8/e/a/8ea09b0b2862ea78ed73cbc0db911563.png)






 dado:
dado: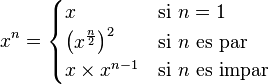
No hay comentarios:
Publicar un comentario