Algoritmos de precisión arbitraria
precisión arbitraria o bignum (por big number, "número grande" en inglés) es un método que permite la representación, en un programa informático, de números ya sean enteros o racionales con tantos dígitos de precisión como cuanto sea deseado y además posibilita la realización de operaciones aritméticas sobre dichos números.
Los números son normalmente almacenados como arrays de dígitos utilizando la base binaria u otra base para la representación. A diferencia de los tipos de datosimplementados en hardware (de una longitud fija determinada por ejemplo por la longitud de los registros de la CPU), los números de precisión arbitraria pueden variar en tamaño, utilizando memoria dinámica.
Si se trata de números fraccionarios se puede representar con arrays separados el denominador y el numerador; o bien utilizar una notación de punto fijo almacenando los dígitos decimales con la precisión deseada; o bien utilizar un formato de punto flotante con un significando multiplicado por un exponente.
Historia e implementaciones
La precisión arbitraria fue implementada por primera vez en MacLisp. Más tarde, el sistema operativo VAX/VMS ofrecía capacidades de precisión arbitraria como una colección de funciones que operaban con cadenas. Hoy en día, bibliotecas bignum están disponibles para los lenguajes de programación más usados. Incluso existen lenguajes diseñados específicamente para cálculo con precisión arbitraria, como por ejemplo el lenguaje de programación bc. Todos los sistemas de álgebra computacional implementan facilidades bignum.
Aplicaciones
Una aplicación común es la criptografía de clave pública, cuyos algoritmos suelen emplear aritmética con enteros de cientos ó miles de dígitos.
También se usa para computar constantes matemáticas fundamentales tales como pi con millones o más dígitos y analizar sus propiedades.
algoritmo de Karatsuba es un procedimiento para multiplicar números grandes eficientemente, que fue descubierto por Anatolii Alexeevitch Karatsuba en 1960 y publicado en 1962.1 2 El algoritmo consigue reducir la múltiplicación de dos números de n dígitos a como máximo 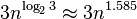 multiplicaciones de un dígito. Es, por lo tanto, más rápido que el algoritmo clásico, que requiere n2 productos de un dígito. Si n = 210 = 1024, en particular, el cómputo final exacto es 310 = 59.049 y (210)2 = 1.048.576, respectivamente.
multiplicaciones de un dígito. Es, por lo tanto, más rápido que el algoritmo clásico, que requiere n2 productos de un dígito. Si n = 210 = 1024, en particular, el cómputo final exacto es 310 = 59.049 y (210)2 = 1.048.576, respectivamente.
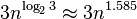 multiplicaciones de un dígito. Es, por lo tanto, más rápido que el algoritmo clásico, que requiere n2 productos de un dígito. Si n = 210 = 1024, en particular, el cómputo final exacto es 310 = 59.049 y (210)2 = 1.048.576, respectivamente.
multiplicaciones de un dígito. Es, por lo tanto, más rápido que el algoritmo clásico, que requiere n2 productos de un dígito. Si n = 210 = 1024, en particular, el cómputo final exacto es 310 = 59.049 y (210)2 = 1.048.576, respectivamente.
El algoritmo de Toom-Cook es una generalización más rápida del de Karatsuba. Para un n suficientemente grande, el algoritmo de Schönhage-Strassen es mejor que el algoritmo de Karatsuba.
El algoritmo de Karatsuba es un claro ejemplo del paradigma divide y vencerás, concretamente del algoritmo de partición binaria. El nombre 'divide y vencerás' se usó por primera vez para éste método .
Historia
El procedimiento estándar para multiplicar dos números de n dígitos requiere un número de operaciones elementales proporcional a n2, o 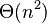 en la Notación O grande. En 1952, Andrey Kolmogorov intentó probar que el algoritmo clásico era óptimo asintóticamente, queriendo demostrar así que cualquier algoritmo para esta tarea requeriría
en la Notación O grande. En 1952, Andrey Kolmogorov intentó probar que el algoritmo clásico era óptimo asintóticamente, queriendo demostrar así que cualquier algoritmo para esta tarea requeriría  operaciones elementales.
operaciones elementales.
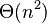 en la Notación O grande. En 1952, Andrey Kolmogorov intentó probar que el algoritmo clásico era óptimo asintóticamente, queriendo demostrar así que cualquier algoritmo para esta tarea requeriría
en la Notación O grande. En 1952, Andrey Kolmogorov intentó probar que el algoritmo clásico era óptimo asintóticamente, queriendo demostrar así que cualquier algoritmo para esta tarea requeriría  operaciones elementales.
operaciones elementales.
En otoño de 1960, Kolmogorov organizó un seminario acerca de problemas matemáticos de cibernética en la Universidad Estatal de Moscú, donde planteó su suposición de  y otros problemas de complejidad computacional. En una semana, Karatsuba, un estudiante de 25 años, encontró un algoritmo divide y vencerásque multiplicaba dos números de n dígitos en
y otros problemas de complejidad computacional. En una semana, Karatsuba, un estudiante de 25 años, encontró un algoritmo divide y vencerásque multiplicaba dos números de n dígitos en 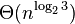 operaciones elementales, refutando así la suposición inicial de Kolmogorov. Kolmogorov se sintió muy desilusionado por tal descubrimiento, y lo hizo público en el que sería su siguiente y último encuentro del seminario.2
operaciones elementales, refutando así la suposición inicial de Kolmogorov. Kolmogorov se sintió muy desilusionado por tal descubrimiento, y lo hizo público en el que sería su siguiente y último encuentro del seminario.2
 y otros problemas de complejidad computacional. En una semana, Karatsuba, un estudiante de 25 años, encontró un algoritmo divide y vencerásque multiplicaba dos números de n dígitos en
y otros problemas de complejidad computacional. En una semana, Karatsuba, un estudiante de 25 años, encontró un algoritmo divide y vencerásque multiplicaba dos números de n dígitos en 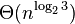 operaciones elementales, refutando así la suposición inicial de Kolmogorov. Kolmogorov se sintió muy desilusionado por tal descubrimiento, y lo hizo público en el que sería su siguiente y último encuentro del seminario.2
operaciones elementales, refutando así la suposición inicial de Kolmogorov. Kolmogorov se sintió muy desilusionado por tal descubrimiento, y lo hizo público en el que sería su siguiente y último encuentro del seminario.2
El método fue publicado en 1962, en la revista científica soviética Proceedings of the USSR Academy of Sciences.1 El artículo había sido escrito por Kolmogorov, posiblemente en colaboración con Yuri Ofman, pero nombraba a "A. Karatsuba y Yu. Ofman" como los autores. Karatsuba solo se dio cuenta de la publicación cuando recibió una copia del artículo por parte de la editorial de la revista.2
Algoritmo
El paso básico
El paso básico del algoritmo de Karatsuba es una fórmula que nos permite calcular el producto de dos números grandes x e y usando tres multiplicaciones de números más pequeños, cada uno con más o menos la mitad de los dígitos de x e y, más algunas sumas y desplazamientos de dígitos.
Supongamos que x e y están representados como cadenas de n dígitos en alguna base B. Para cualquier entero positivo m menor que n, uno puede dividir los dos números dados de la manera siguiente:
- x = x1Bm + x0
- y = y1Bm + y0
donde x0 e y0 son menores que Bm. El producto es, entonces:
- xy = (x1Bm + x0)(y1Bm + y0)
- = z2 B2m + z1 Bm + z0
donde
- z2 = x1y1
- z1 = x1y0 + x0y1
- z0 = x0y0
Estas fórmulas requieren cuatro multiplicaciones. Karatsuba observó que podemos calcular xy en solo tres multiplicaciones, por el coste de unas sumas adicionales:
- Supongamos z2 = x1y1
- Supongamos z0 = x0y0
- Supongamos z1 = (x1 + x0)(y1 + y0) − z2 − z0
ya que
- z1 = (x1y1 + x1y0 + x0y1 + x0y0) - x1y1 - x0y0 = x1y0 + x0y1
Si y1 = 0, solo hay que realizar dos multiplicaciones puesto que:
- z2 = 0
- z0 = x0y0
- z1 = x1y0
Ejemplo
Digamos que queremos calcular el producto de 1234 con 5678. Elegimos la base 10 (B = 10) y m = 2. Entonces tenemos:
- 12 34 = 12 × 102 + 34
- 56 78 = 56 × 102 + 78
- z2 = 12 × 56 = 672
- z0 = 34 × 78 = 2652
- z1 = (12 + 34)(56 + 78) − z2 − z0 = 46 × 134 − 672 − 2652 = 2840
- resultado = z2 × 102×2 + z1 × 102 + z0 = 672 × 10000 + 2840 × 100 + 2652 = 7006652
Aplicación recursiva
Si n es cuatro o mayor que cuatro, las tres multiplicaciones en el paso básico de Karatsuba suponen operandos con menos de n dígitos. Por lo tanto, estos productos pueden ser calculados por llamadas recursivas del algoritmo de Karatsuba. La recursividad puede ser aplicada hasta que los números sean tan pequeños que pueden (o deben) ser calculados directamente.
En un ordenador con un multiplicador ALU completo de 32 x 32 bits, por ejemplo, uno podría escoger B = 231 = 2,147,483,648 o B = 109 = 1,000,000,000, y almacenar cada dígito como una palabra binaria de 32 bits. Entonces las sumas x1 + x0 e y1 + y0 no necesitarán un dígito de acarreo extra (como en un sumador sin acarreo (carry-save adder)), y la recurrencia de Karatsuba puede ser aplicada hasta que los números tengan solo un dígito.
Análisis de eficiencia
El paso básico de Karatsuba funciona para cualquier base B y cualquier m. pero el algoritmo recursivo es más eficiente cuando m es igual a n/2, redondeado por exceso. En particular, si n es 2k, para un entero k, y la recursividad se para solo cuando n es 1, entonces el número de multiplicaciones de un solo dígito es 3k, es decir, nc dondec = log23.
Ya que uno puede ampliar cualquier entrada con dígitos cero hasta que su longitud sea una potencia de dos, se tiene que el número de multiplicaciones elementales, para cualquier n, es a lo sumo 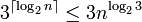 .
.
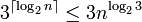 .
.
Ya que las sumas, las restas, y los desplazamientos de dígitos (multiplicaciones por potencias de B) en el paso básico de Karatsuba requieren tiempos proporcionales an, su coste se hace insignificante a medida que crece n. Precisamente, si t(n) denota el número total de operaciones elementales que el algoritmo realiza cuando se multiplican dos números de n dígitos, entonces podemos escribir:
- t(n) = 3 t(
 n/2
n/2 ) + cn + d
) + cn + d
para algunas constantes c y d. Para esta relación de recurrencia, el Teorema Maestro da la cota superior asintótica t(n) =  (nlog(3)/log(2)).
(nlog(3)/log(2)).
 (nlog(3)/log(2)).
(nlog(3)/log(2)).
Se tiene que, para un n suficientemente grande, el algoritmo de Karatsuba realizará menos desplazamientos y sumas de un solo dígito que la multiplicación a mano, incluso cuando su paso básico use más sumas y desplazamientos que la fórmula sencilla. Para valores pequeños de n, sin embargo, los desplazamientos y operaciones de suma pueden hacerlo ir más lentamente que el método a mano. Todo depende de la plataforma del ordenador y del contexto. Por norma general, Karatsuba normalmente más rápido cuando los multiplicandos son del orden 2320 ≈ 2×1096 o mayor [1][2]
Imaginemos que tenemos 2 números 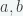 con una cantidad muy grande de dígitos. Debido a las limitaciones de nuestro sistema computacional, no es posible multiplicar directamente y obtener el resultado
con una cantidad muy grande de dígitos. Debido a las limitaciones de nuestro sistema computacional, no es posible multiplicar directamente y obtener el resultado  , es decir, un programa simple como
, es decir, un programa simple como
1
2
3
4
5
6
7
8
9
10
11
| #include using namespace std;int main(){ long double a, b; cin >> a; cin >> b; cout << a*b << endl; return 0;} |
no es capaz de hacer la multiplicación, pues recordemos que si las variables 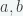 son del tipo long double, tenemos que
son del tipo long double, tenemos que
pero es claro que lo anterior no necesariamente es cierto, de hecho, basta tomar  y
y  como cualquiera de las cotas anteriores para que el producto se salga de este rango, lo que provoca que el programa no pueda hacer el producto y no lo intente (generalmente arroja un “error de segmentación”). La forma correcta de hacerlo y de intentar esquivar las limitaciones que tiene un ordenador es tratar los números como arreglos. Por ejemplo, en base 10 podemos hacer una correspondencia entre el número 981 y el arreglo cuya coordenada 2 es el 9, la coordenada 1 es el 8 y la coordenada 0 es el 1 (la correspondencia se puede hacer al reves para que la posición en el arreglo coincida con la potencia de 10 en la descomposición decimal). Por supuesto que lo más óptimo es usar la mayor base posible para así disminuir la dimensión del arreglo que almacena al número, sin embargo, para no complicar mucho más las cosas trabajaremos en este post solo con la base 10. Con lo ya dicho, podemos hacernos una idea de la necesidad de utilizar algoritmos que operen arreglos como si estos fueran grandes números; particularmente, la multiplicación es una operación simple que se complica bastante cuando intentamos esquivar las limitaciones del ordenador, y más aún, cuando intentamos minimizar el tiempo de ejecución del algoritmo. Lo que intentaré explicarles ahora será el funcionamiento de uno de los algoritmos “rápidos” existentes para multiplicar números enormemente grandes. A continuación puntualizamos las ideas que definen al algoritmo de Karatsuba:
como cualquiera de las cotas anteriores para que el producto se salga de este rango, lo que provoca que el programa no pueda hacer el producto y no lo intente (generalmente arroja un “error de segmentación”). La forma correcta de hacerlo y de intentar esquivar las limitaciones que tiene un ordenador es tratar los números como arreglos. Por ejemplo, en base 10 podemos hacer una correspondencia entre el número 981 y el arreglo cuya coordenada 2 es el 9, la coordenada 1 es el 8 y la coordenada 0 es el 1 (la correspondencia se puede hacer al reves para que la posición en el arreglo coincida con la potencia de 10 en la descomposición decimal). Por supuesto que lo más óptimo es usar la mayor base posible para así disminuir la dimensión del arreglo que almacena al número, sin embargo, para no complicar mucho más las cosas trabajaremos en este post solo con la base 10. Con lo ya dicho, podemos hacernos una idea de la necesidad de utilizar algoritmos que operen arreglos como si estos fueran grandes números; particularmente, la multiplicación es una operación simple que se complica bastante cuando intentamos esquivar las limitaciones del ordenador, y más aún, cuando intentamos minimizar el tiempo de ejecución del algoritmo. Lo que intentaré explicarles ahora será el funcionamiento de uno de los algoritmos “rápidos” existentes para multiplicar números enormemente grandes. A continuación puntualizamos las ideas que definen al algoritmo de Karatsuba:
- Sean
dos enteros de
dígitos (
par);
- Definimos
;
- Divimos
en 2 números:
(que corresponde a los
dígitos de la derecha) y
(que corresponde a los
dígitos de la izquierda);
- Del mismo modo dividimos
en
y
;
- Calculamos
,
y
;
- Retornamos
;
Este es el método básico de descomposición que propone el algoritmo, pero suele ocurrir que los números 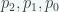 siguen siendo demasiado grandes como para operarlos, por lo que ellos se deben descomponer de la misma forma, obteniendo ciertos números
siguen siendo demasiado grandes como para operarlos, por lo que ellos se deben descomponer de la misma forma, obteniendo ciertos números ![[p_2]_2, [p_2]_1, [p_2]_0, [p_1]_2, [p_1]_1, [p_1]_0, [p_0]_2, [p_0]_1, [p_0]_0 [p_2]_2, [p_2]_1, [p_2]_0, [p_1]_2, [p_1]_1, [p_1]_0, [p_0]_2, [p_0]_1, [p_0]_0](https://s0.wp.com/latex.php?latex=%5Bp_2%5D_2%2C+%5Bp_2%5D_1%2C+%5Bp_2%5D_0%2C+%5Bp_1%5D_2%2C+%5Bp_1%5D_1%2C+%5Bp_1%5D_0%2C+%5Bp_0%5D_2%2C+%5Bp_0%5D_1%2C+%5Bp_0%5D_0&bg=f2f7f7&fg=333333&s=0) , los cuales podrían tener el mismo problema y sea necesario descomponer nuevamente (la cantidad de valores aumenta exponencialmente)… la idea es dejar el producto
, los cuales podrían tener el mismo problema y sea necesario descomponer nuevamente (la cantidad de valores aumenta exponencialmente)… la idea es dejar el producto 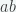 en función de valores lo suficientemente pequeños como para trabajar con ellos “sin importar mucho la cantidad de operaciones que se hagan” (se supone que aumentar la cantidad de operaciones nos permite llegar resultado final). A continuación les dejo un programa en C++ que implementa el algoritmo de Karatsuba; este programa viene acompañado de otro programa que genera aleatoriamente números gigantezcos (nosotros tardaríamos mucho en escribir 2 números de 1000 cifras manualmente) que me permitió estudiar el rendimiento y el tiempo de ejecución del algoritmo dependiendo de lo grande que son los números a multiplicar (un punto realmente muy interesante, pero que no abordaremos en este post):
en función de valores lo suficientemente pequeños como para trabajar con ellos “sin importar mucho la cantidad de operaciones que se hagan” (se supone que aumentar la cantidad de operaciones nos permite llegar resultado final). A continuación les dejo un programa en C++ que implementa el algoritmo de Karatsuba; este programa viene acompañado de otro programa que genera aleatoriamente números gigantezcos (nosotros tardaríamos mucho en escribir 2 números de 1000 cifras manualmente) que me permitió estudiar el rendimiento y el tiempo de ejecución del algoritmo dependiendo de lo grande que son los números a multiplicar (un punto realmente muy interesante, pero que no abordaremos en este post):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
| #include #include #include #include using namespace std;#define MIN_EXP 1void karatsuba(unsigned char *a, unsigned char *b, unsigned char *ret, int d);void Multiplicacion_usual(unsigned char *a, unsigned char *b, unsigned char *ret, int d);void Acarreo(unsigned char *a, int d);void Obtener_Num(unsigned char *a, int *largo_a, int MAX_DIGITS);void Mostrar(unsigned char *a, int d);int main(int argc, char **argv){ int pri, sec, y, D ; pri=atoi(argv[1]); sec=atoi(argv[2]); y = (pri > sec) ? pri : sec; for(D=1; D int MAX_DIGITS=D; unsigned char * a = new unsigned char [MAX_DIGITS]; unsigned char * b = new unsigned char [MAX_DIGITS]; unsigned char * r = new unsigned char [6*MAX_DIGITS]; int largo_a, largo_b, d, i ; clock_t start; clock_t stop; Obtener_Num(a, &largo_a, MAX_DIGITS); Obtener_Num(b, &largo_b, MAX_DIGITS); if(largo_a<0 || largo_b<0) { printf("0\n"); exit(0); return 0; } i = (largo_a > largo_b) ? largo_a : largo_b; for(d=1; d for(i=largo_a; i { a[i]=0; } for(i=largo_b; i { b[i]=0; } start = clock(); stop = start + CLOCKS_PER_SEC; for(i=0; clock() { karatsuba(a, b, r, d); Acarreo(r, 2*d); } start = clock() - start; Mostrar(r, 2*d); printf(" %f [seg] (%d iteraciones)\n", (double) start / CLOCKS_PER_SEC / i, i); delete [] a; delete [] b; delete [] r;}void karatsuba(unsigned char *a, unsigned char *b, unsigned char *ret, int d){ int i ; unsigned char *ar = &a[0]; unsigned char *al = &a[d/2]; unsigned char *br = &b[0]; unsigned char *bl = &b[d/2]; unsigned char *asum = &ret[d*5]; unsigned char *bsum = &ret[d*5+d/2]; unsigned char *x1 = &ret[d*0]; unsigned char *x2 = &ret[d*1]; unsigned char *x3 = &ret[d*2]; if(d <= MIN_EXP) { Multiplicacion_usual(a, b, ret, d); return; } for(i=0; i { asum[i]=al[i]+ar[i]; bsum[i]=bl[i]+br[i]; } karatsuba(ar, br, x1, d/2); karatsuba(al, bl, x2, d/2); karatsuba(asum, bsum, x3, d/2); for(i=0; i { x3[i]=x3[i]-x1[i]-x2[i]; } for(i=0; i { ret[i+d/2]+=x3[i]; }}void Multiplicacion_usual(unsigned char *a, unsigned char *b, unsigned char *ret, int d){ int i, j ; for(i=0; i<2*d; i++) { ret[i]=0; } for(i=0; i { for(j=0; j { ret[i+j]+=a[i]*b[j]; } }}void Acarreo(unsigned char *a, int d){ int c=0, i ; for(i=0; i { a[i]+=c; if(a[i] < 0) { c=-(-(a[i]+1)/10+1); } else { c = a[i] / 10; } a[i] -= c * 10; }}void Obtener_Num(unsigned char *a, int *largo_a, int MAX_DIGITS){ int c, i ; *largo_a = 0; while(true) { c=getchar(); if(c=='\n' || c==EOF) { break; } if(*largo_a>=MAX_DIGITS) { while(c!='\n' && c!=EOF) { c=getchar(); } } a[*largo_a]=c-'0'; ++(*largo_a); } for(i=0; i*2<*largo_a-1; i++) { c=a[i]; a[i]=a[*largo_a-i-1]; a[*largo_a-i-1]=c; }}void Mostrar(unsigned char *a, int d){ int i; for(i=d-1; i>0; i--) { if(a[i]!=0) { break; } } for(; i >= 0; i--) { printf("%d", a[i]); }} |
Para quienes no lo sepan, “acarreo” es el nombre que suele darse a la “reserva” (como en la suma) en un algoritmo matemático. Si “karatsuba” es el nombre del ejecutable (luego de compilar y suponiendo que todo se encuentra en la carpeta HOME), la forma de ejecutar el programa sería “./karatsuba N1 N2” (esto en la consola de Linux), donde N1 y N2 son los números que deseamos multiplicar. Si el resultado del producto es demasiado grande, suele guardarse el resultado directamente en un archivo, digamos “producto.dat”, usando la siguiente línea: “./karatsuba N1 N2 > producto.dat “.
No hay comentarios:
Publicar un comentario