Algoritmos de clasificación
En el campo del aprendizaje automático, el objetivo del aprendizaje supervisado es usar las características de un objeto para identificar a qué clase (o grupo) pertenece. Un clasificador lineal logra esto tomando una decisión de clasificación basada en el valor de una combinación lineal de sus características. Las características de un objeto son típicamente presentadas en un vector llamado vector de características.
Definición
Si la entrada del clasificador es un vector de características reales 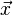 , entonces el resultado de salida es
, entonces el resultado de salida es
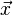 , entonces el resultado de salida es
, entonces el resultado de salida es
donde  es un vector real de pesos y f es una función que convierte el producto punto a punto de los dos vectores en la salida deseada. El vector de pesos
es un vector real de pesos y f es una función que convierte el producto punto a punto de los dos vectores en la salida deseada. El vector de pesos  aprende de un conjunto de muestras de entrenamiento. A menudo f es una función simple que mapea todos los valores por encima de un cierto umbral a la primera clase y el resto a la segunda clase. Una f más compleja puede dar la probabilidad de que una muestra pertenezca a cierta clase.
aprende de un conjunto de muestras de entrenamiento. A menudo f es una función simple que mapea todos los valores por encima de un cierto umbral a la primera clase y el resto a la segunda clase. Una f más compleja puede dar la probabilidad de que una muestra pertenezca a cierta clase.
 es un vector real de pesos y f es una función que convierte el producto punto a punto de los dos vectores en la salida deseada. El vector de pesos
es un vector real de pesos y f es una función que convierte el producto punto a punto de los dos vectores en la salida deseada. El vector de pesos  aprende de un conjunto de muestras de entrenamiento. A menudo f es una función simple que mapea todos los valores por encima de un cierto umbral a la primera clase y el resto a la segunda clase. Una f más compleja puede dar la probabilidad de que una muestra pertenezca a cierta clase.
aprende de un conjunto de muestras de entrenamiento. A menudo f es una función simple que mapea todos los valores por encima de un cierto umbral a la primera clase y el resto a la segunda clase. Una f más compleja puede dar la probabilidad de que una muestra pertenezca a cierta clase.
Para un problema de dos clases, se puede visualizar la operación de un clasificador lineal como una partición del espacion de alta dimensionalidad de entrada con unhiperplano: todos los puntos a un lado del hiperplano son clasificados como "sí", mientras que los demás son clasificados como "no".
Los clasificadores lineales se suelen usar en situaciones donde la velocidad de la clasificación es importante, ya que a menudo es el clasificador más rápido, especialmente cuando 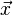 es disperso. Sin embargo, los árboles de decisión pueden ser más rápidos. Además, los clasificadores lineales con frecuencia funcionan muy bien cuando el número de dimensiones de
es disperso. Sin embargo, los árboles de decisión pueden ser más rápidos. Además, los clasificadores lineales con frecuencia funcionan muy bien cuando el número de dimensiones de 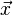 es grande, como en clasificación de documentos, donde típicamente cada elemento en
es grande, como en clasificación de documentos, donde típicamente cada elemento en 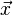 es el número de apariciones de una palabra en un documento. En tales casos, el clasificador debe estar bien regularizado.
es el número de apariciones de una palabra en un documento. En tales casos, el clasificador debe estar bien regularizado.
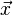 es disperso. Sin embargo, los árboles de decisión pueden ser más rápidos. Además, los clasificadores lineales con frecuencia funcionan muy bien cuando el número de dimensiones de
es disperso. Sin embargo, los árboles de decisión pueden ser más rápidos. Además, los clasificadores lineales con frecuencia funcionan muy bien cuando el número de dimensiones de 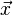 es grande, como en clasificación de documentos, donde típicamente cada elemento en
es grande, como en clasificación de documentos, donde típicamente cada elemento en 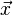 es el número de apariciones de una palabra en un documento. En tales casos, el clasificador debe estar bien regularizado.
es el número de apariciones de una palabra en un documento. En tales casos, el clasificador debe estar bien regularizado.Modelo generativo vs. modelo discriminativo
Hay dos tipos de clases de métodos para determinar los parámetros de un clasificador lineal  .1 2 Métodos de la primera clase conditional density functions
.1 2 Métodos de la primera clase conditional density functions  . Ejemplos de tales algoritmos incluyen:
. Ejemplos de tales algoritmos incluyen:
 .1 2 Métodos de la primera clase conditional density functions
.1 2 Métodos de la primera clase conditional density functions  . Ejemplos de tales algoritmos incluyen:
. Ejemplos de tales algoritmos incluyen:- Linear Discriminant Analysis (or Fisher's linear discriminant) (LDA)—assumes Gaussian conditional density models
- Naive Bayes classifier—assumes independent binomial conditional density models.
The second set of methods includes discriminative models, which attempt to maximize the quality of the output on a training set. Additional terms in the training cost function can easily perform regularization of the final model. Examples of discriminative training of linear classifiers include
- Logistic regression—maximum likelihood estimation of
 assuming that the observed training set was generated by a binomial model that depends on the output of the classifier.
assuming that the observed training set was generated by a binomial model that depends on the output of the classifier. - Perceptrón—an algorithm that attempts to fix all errors encountered in the training set
- Support vector machine—an algorithm that maximizes the margin between the decision hyperplane and the examples in the training set.
Note: Despite its name, LDA does not belong to the class of discriminative models in this taxonomy. However, its name makes sense when we compare LDA to the other main linear dimensionality reduction algorithm: Principal Components Analysis (PCA). LDA is a supervised learning algorithm that utilizes the labels of the data, while PCA is an unsupervised learning algorithm that ignores the labels. To summarize, the name is a historical artifact (see,3 p.117).
Discriminative training often yields higher accuracy than modeling the conditional density functions. However, handling missing data is often easier with conditional density models.
All of the linear classifier algorithms listed above can be converted into non-linear algorithms operating on a different input space  , using the kernel trick.
, using the kernel trick.
 , using the kernel trick.
, using the kernel trick.
clasificadores lineales .- ....................................................:https://fdoperez.webs.ull.es/doc/recpat4.pdf
 -nn (K nearest neighbors Fix y Hodges, 19511 ) es un método de clasificación supervisada (Aprendizaje, estimación basada en un conjunto de entrenamiento y prototipos) que sirve para estimar la función de densidad
-nn (K nearest neighbors Fix y Hodges, 19511 ) es un método de clasificación supervisada (Aprendizaje, estimación basada en un conjunto de entrenamiento y prototipos) que sirve para estimar la función de densidad  de las predictoras
de las predictoras  por cada clase
por cada clase  .
.
Este es un método de clasificación no paramétrico, que estima el valor de la función de densidad de probabilidad o directamente la probabilidad a posteriori de que un elemento  pertenezca a la clase
pertenezca a la clase  a partir de la información proporcionada por el conjunto de prototipos. En el proceso de aprendizaje no se hace ninguna suposición acerca de la distribución de las variables predictoras.
a partir de la información proporcionada por el conjunto de prototipos. En el proceso de aprendizaje no se hace ninguna suposición acerca de la distribución de las variables predictoras.
 pertenezca a la clase
pertenezca a la clase  a partir de la información proporcionada por el conjunto de prototipos. En el proceso de aprendizaje no se hace ninguna suposición acerca de la distribución de las variables predictoras.
a partir de la información proporcionada por el conjunto de prototipos. En el proceso de aprendizaje no se hace ninguna suposición acerca de la distribución de las variables predictoras.
En el reconocimiento de patrones, el algoritmo  -nn es usado como método de clasificación de objetos (elementos) basado en un entrenamiento mediante ejemplos cercanos en el espacio de los elementos.
-nn es usado como método de clasificación de objetos (elementos) basado en un entrenamiento mediante ejemplos cercanos en el espacio de los elementos.  -nn es un tipo de "Lazy Learning" (en), donde la función se aproxima solo localmente y todo el cómputo es diferido a la clasificación.
-nn es un tipo de "Lazy Learning" (en), donde la función se aproxima solo localmente y todo el cómputo es diferido a la clasificación.
 -nn es usado como método de clasificación de objetos (elementos) basado en un entrenamiento mediante ejemplos cercanos en el espacio de los elementos.
-nn es usado como método de clasificación de objetos (elementos) basado en un entrenamiento mediante ejemplos cercanos en el espacio de los elementos.  -nn es un tipo de "Lazy Learning" (en), donde la función se aproxima solo localmente y todo el cómputo es diferido a la clasificación.
-nn es un tipo de "Lazy Learning" (en), donde la función se aproxima solo localmente y todo el cómputo es diferido a la clasificación.Algoritmo
Los ejemplos de entrenamiento son vectores en un espacio característico multidimensional, cada ejemplo está descrito en términos de  atributos considerando
atributos considerando  clases para la clasificación. Los valores de los atributos del
clases para la clasificación. Los valores de los atributos del  -esimo ejemplo (donde
-esimo ejemplo (donde 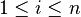 ) se representan por el vector
) se representan por el vector  -dimensional
-dimensional
 atributos considerando
atributos considerando  clases para la clasificación. Los valores de los atributos del
clases para la clasificación. Los valores de los atributos del  -esimo ejemplo (donde
-esimo ejemplo (donde 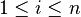 ) se representan por el vector
) se representan por el vector  -dimensional
-dimensional
El espacio es particionado en regiones por localizaciones y etiquetas de los ejemplos de entrenamiento. Un punto en el espacio es asignado a la clase  si esta es la clase más frecuente entre los k ejemplos de entrenamiento más cercano. Generalmente se usa la distancia euclidiana.
si esta es la clase más frecuente entre los k ejemplos de entrenamiento más cercano. Generalmente se usa la distancia euclidiana.
 si esta es la clase más frecuente entre los k ejemplos de entrenamiento más cercano. Generalmente se usa la distancia euclidiana.
si esta es la clase más frecuente entre los k ejemplos de entrenamiento más cercano. Generalmente se usa la distancia euclidiana.
La fase de entrenamiento del algoritmo consiste en almacenar los vectores característicos y las etiquetas de las clases de los ejemplos de entrenamiento. En la fase de clasificación, la evaluación del ejemplo (del que no se conoce su clase) es representada por un vector en el espacio característico. Se calcula la distancia entre los vectores almacenados y el nuevo vector, y se seleccionan los  ejemplos más cercanos. El nuevo ejemplo es clasificado con la clase que más se repite en los vectores seleccionados.
ejemplos más cercanos. El nuevo ejemplo es clasificado con la clase que más se repite en los vectores seleccionados.
 ejemplos más cercanos. El nuevo ejemplo es clasificado con la clase que más se repite en los vectores seleccionados.
ejemplos más cercanos. El nuevo ejemplo es clasificado con la clase que más se repite en los vectores seleccionados.
Este método supone que los vecinos más cercanos nos dan la mejor clasificación y esto se hace utilizando todos los atributos; el problema de dicha suposición es que es posible que se tengan muchos atributos irrelevantes que dominen sobre la clasificación: dos atributos relevantes perderían peso entre otros veinte irrelevantes.
Para corregir el posible sesgo se puede asignar un peso a las distancias de cada atributo, dándole así mayor importancia a los atributos más relevantes. Otra posibilidad consiste en tratar de determinar o ajustar los pesos con ejemplos conocidos de entrenamiento. Finalmente, antes de asignar pesos es recomendable identificar y eliminar los atributos que se consideran irrelevantes.
En síntesis, el método  -nn se resumen en dos algoritmos:
-nn se resumen en dos algoritmos:
 -nn se resumen en dos algoritmos:
-nn se resumen en dos algoritmos:Algoritmo de entrenamiento
Para cada ejemplo  ,donde
,donde  , agregar el ejemplo a la estructura representando los ejemplos de aprendizaje.
, agregar el ejemplo a la estructura representando los ejemplos de aprendizaje.
 ,donde
,donde  , agregar el ejemplo a la estructura representando los ejemplos de aprendizaje.
, agregar el ejemplo a la estructura representando los ejemplos de aprendizaje.Algoritmo de clasificación
Dado un ejemplar 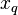 que debe ser clasificado, sean
que debe ser clasificado, sean  los
los  vecinos más cercanos a
vecinos más cercanos a 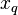 en los ejemplos de aprendizaje, regresar
en los ejemplos de aprendizaje, regresar
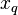 que debe ser clasificado, sean
que debe ser clasificado, sean  los
los  vecinos más cercanos a
vecinos más cercanos a 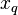 en los ejemplos de aprendizaje, regresar
en los ejemplos de aprendizaje, regresar
donde

el valor 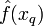 devuelto por el algoritmo como un estimador de
devuelto por el algoritmo como un estimador de  es solo el valor más común de
es solo el valor más común de  entre los
entre los  vecinos más cercanos a
vecinos más cercanos a 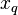 . Si elegimos
. Si elegimos 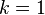 ; entonces el vecino más cercano a
; entonces el vecino más cercano a  determina su valor.
determina su valor.
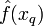 devuelto por el algoritmo como un estimador de
devuelto por el algoritmo como un estimador de  es solo el valor más común de
es solo el valor más común de  entre los
entre los  vecinos más cercanos a
vecinos más cercanos a 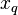 . Si elegimos
. Si elegimos 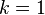 ; entonces el vecino más cercano a
; entonces el vecino más cercano a  determina su valor.
determina su valor.
Elección del 
La mejor elección de  depende fundamentalmente de los datos; generalmente, valores grandes de
depende fundamentalmente de los datos; generalmente, valores grandes de  reducen el efecto de ruido en la clasificación, pero crean límites entre clases parecidas. Un buen
reducen el efecto de ruido en la clasificación, pero crean límites entre clases parecidas. Un buen  puede ser seleccionado mediante una optimización de uso. El caso especial en que la clase es predicha para ser la clase más cercana al ejemplo de entrenamiento (cuando
puede ser seleccionado mediante una optimización de uso. El caso especial en que la clase es predicha para ser la clase más cercana al ejemplo de entrenamiento (cuando 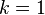 ) es llamada Nearest Neighbor Algorithm, Algoritmo del vecino más cercano.
) es llamada Nearest Neighbor Algorithm, Algoritmo del vecino más cercano.
 depende fundamentalmente de los datos; generalmente, valores grandes de
depende fundamentalmente de los datos; generalmente, valores grandes de  reducen el efecto de ruido en la clasificación, pero crean límites entre clases parecidas. Un buen
reducen el efecto de ruido en la clasificación, pero crean límites entre clases parecidas. Un buen  puede ser seleccionado mediante una optimización de uso. El caso especial en que la clase es predicha para ser la clase más cercana al ejemplo de entrenamiento (cuando
puede ser seleccionado mediante una optimización de uso. El caso especial en que la clase es predicha para ser la clase más cercana al ejemplo de entrenamiento (cuando 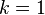 ) es llamada Nearest Neighbor Algorithm, Algoritmo del vecino más cercano.
) es llamada Nearest Neighbor Algorithm, Algoritmo del vecino más cercano.
La exactitud de este algoritmo puede ser severamente degradada por la presencia de ruido o características irrelevantes, o si las escalas de características no son consistentes con lo que uno considera importante. Muchas investigaciones y esfuerzos fueron puestos en la selección y crecimiento de características para mejorar las clasificaciones. Particularmente una aproximación en el uso de algoritmos que evolucionan para optimizar características de escalabilidad. Otra aproximación consiste en escalar características por la información mutua de los datos de entrenamiento con las clases de entrenamiento.
Posibles variantes del algoritmo básico
Vecinos más cercanos con distancia ponderada
Se puede ponderar la contribución de cada vecino de acuerdo a la distancia entre él y el ejemplar a ser clasificado 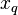 , dando mayor peso a los vecinos más cercanos. Por ejemplo podemos ponderar el voto de cada vecino de acuerdo al cuadrado inverso de sus distancias
, dando mayor peso a los vecinos más cercanos. Por ejemplo podemos ponderar el voto de cada vecino de acuerdo al cuadrado inverso de sus distancias
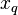 , dando mayor peso a los vecinos más cercanos. Por ejemplo podemos ponderar el voto de cada vecino de acuerdo al cuadrado inverso de sus distancias
, dando mayor peso a los vecinos más cercanos. Por ejemplo podemos ponderar el voto de cada vecino de acuerdo al cuadrado inverso de sus distancias
donde
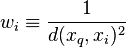
De esta manera se ve que no hay riesgo de permitir a todos los ejemplos entrenamiento contribuir a la clasificación de 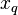 , ya que al ser muy distantes no tendrían peso asociado. La desventaja de considerar todos los ejemplos seria su lenta respuesta (método global). Se quiere siempre tener un método local en el que solo los vecinos más cercanos son considerados.
, ya que al ser muy distantes no tendrían peso asociado. La desventaja de considerar todos los ejemplos seria su lenta respuesta (método global). Se quiere siempre tener un método local en el que solo los vecinos más cercanos son considerados.
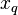 , ya que al ser muy distantes no tendrían peso asociado. La desventaja de considerar todos los ejemplos seria su lenta respuesta (método global). Se quiere siempre tener un método local en el que solo los vecinos más cercanos son considerados.
, ya que al ser muy distantes no tendrían peso asociado. La desventaja de considerar todos los ejemplos seria su lenta respuesta (método global). Se quiere siempre tener un método local en el que solo los vecinos más cercanos son considerados.
Esta mejora es muy efectiva en muchos problemas prácticos. Es robusto ante los ruidos de datos y suficientemente efectivo en conjuntos de datos grandes. Se puede ver que al tomar promedios ponderados de los  vecinos más cercanos el algoritmo puede evitar el impacto de ejemplos con ruido aislados.
vecinos más cercanos el algoritmo puede evitar el impacto de ejemplos con ruido aislados.
 vecinos más cercanos el algoritmo puede evitar el impacto de ejemplos con ruido aislados.
vecinos más cercanos el algoritmo puede evitar el impacto de ejemplos con ruido aislados.
Regla de los k vecino más cercano (k-NN Nearest Neighbour) es otro clasificador supervisado basado en Reconocimiento de patrones criterios de vecindad, y también se conoce como algoritmo de clasificación ``k-NN``. Parte de la idea de que una nueva muestra será clasificada a la clase a la cual pertenezca la mayor cantidad de vecinos más cercanos del [Reconocimiento de patrones patrón] del conjunto de entrenamiento más cercano a ésta.
Contenido
[ocultar]Regla ``k`-NN`
Al aplicar la regla NN, se explora todo el conocimiento almacenado en el conjunto de entrenamiento para determinar cuál será la clase a la que pertenece una nueva muestra, pero únicamente tiene en cuenta el vecino más próximo a ella, por lo que es lógico pensar que es posible que no se esté aprovechando de forma eficiente toda la información que se podría extraer del conjunto de entrenamiento.
Con el objetivo de resolver esta posible deficiencia surge la regla de los k vecinos más cercanos (k-NN). La regla k-NN es una extensión de la regla NN, en la que se utiliza la información suministrada por los k prototipos del conjunto de entrenamiento más cercanos de una nueva muestra para su clasificación.
Formalmente se define la vecindad de los k vecinos más cercanos de una muestra x como:
Definición de vecindad
Sea un conjunto de entrenamiento de N prototipos pertenecientes a M clases distintas, E el Reconocimiento de patrones espacio de representación de los objetos y x una muestra (). Se define como vecindad al conjunto de prototipos del conjunto de entrenamiento que cumple las tres condiciones siguientes:
La expresión anterior significa que la regla k-NN determina que la clase a la cual pertenece una nueva muestra x es la más votada por sus k vecinos más cercanos.
Ejemplo de funcionamiento
En la imagen superior se ilustra el funcionamiento de esta regla de clasificación. En ella se encuentran representadas 12 muestras pertenecientes a dos clases distintas: la Clase 1 está formada por 6 cuadrados de color azul y la Clase 2 formada por 6 círculos de color rojo. En este ejemplo, se han seleccionado tres vecinos, es decir, (k=3).
De los 3 vecinos más cercanos a la muestra x, representada en la figura por una cruz, uno de ellos pertenece a la Clase 1 y los otros dos a la Clase 2. Por tanto, la regla 3-NN asignará la muestra x a la Clase 2. Es importante señalar que si se hubiese utilizado como regla de clasificación la NN, la muestra x sería asignada a la Clase 1, pues el vecino más cercano de la muestra x pertenece a la Clase 1.
Ventajas y limitantes
En problemas prácticos donde se aplica esta regla de clasificación se acostumbra tomar un número k de vecinos impar para evitar posibles empates, aunque esta forma es cierta en problemas que poseen dos clases nada más. También, los empates pueden ser resueltos decidiendo aleatoriamente la clasificación de la muestra entre las clases empatadas o la clase donde la distancia media de sus vecinos sea inferior.
Para determinados problemas reales (es decir, con un número finito de muestras e incluso, en muchas ocasiones, un número relativamente pequeño), la aplicación de esta regla podría entenderse como una solución poco apropiada, debido a los pobres resultados que pudieran obtener, es decir, a su baja tasa de aciertos en el correspondiente proceso de clasificación. Este problema también está presente cuando el número de muestras de que se dispone puede considerarse pequeño comparado con la dimensionalidad intrínseca del espacio de representación, lo cual corresponde a una situación bastante habitual.


No hay comentarios:
Publicar un comentario