Algoritmos de factorización de enteros
criba cuadrática (QS del inglés quadratic sieve), es un algoritmo de factorización de enteros y, en la práctica, el segundo método más rápido conocido (después de la criba general del cuerpo de números). Es todavía el más rápido para enteros que tienen 100 o menos dígitos decimales, y es considerado mucho más sencillo que la criba de cuerpos numéricos. Es un algoritmo de factorización de propósito general, lo que significa que su tiempo de ejecución únicamente depende el tamaño del entero a ser factorizado, y no sobre una estructura especial o propiedades. Fue inventado por Carl Pomerance en 1981 como una mejora a la criba lineal de Schroeppel.
Tabla 1: factorización usando la criba cuadrática
Año
|
nº de dígitos decimales
|
cuántas veces más difícil
|
factorizados
|
factorizar un número de 512 bits
| |
1983
|
71
|
> 20 millones
|
1985
|
80
|
< 2 millones
|
1988
|
90
|
250.000
|
1989
|
100
|
30.000
|
1993
|
120
|
500
|
1994
|
129
|
100
|
Estos números son algo escalofriantes. Hoy no es raro ver números de 512 bits usados en sistemas operacionales. Factorizarlos, y por tanto comprometer su seguridad, está bien dentro del rango de posibilidades: un gusano durante un fin de semana en Internet podría hacerlo.
La potencia de computación se mide habitualmente en mips-año: un ordenador de un millón de instrucciones por segundo, funcionando durante un año, o unas 3*10^13 instrucciones. Por convención, una máquina de 1 mips es equivalente al DEC VAX 11/780. Por tanto, un mips-año es un VAX 11/780 funcionando durante un año, o su equivalente
La factorización de un número de 71 dígitos requirió 0.1 mips-años; la factorización de un número de 129 dígitos en 1994 requirió 5000. Este incremento dramático en potencia de cómputo resultó fundamentalmente de la introducción de cómputo distribuido, usando el tiempo inerte de una red de estaciones de trabajo. La factorización de 1983 usó 9.5 horas de CPU en un único Cray X-MP; la factorización de 1994 usó el tiempo muerto de 1600 ordenadores a lo largo del mundo durante unos ocho meses. Los métodos modernos de factorización se prestan a esta clase de implementación distribuida.
El cuadro se hace aún peor. Un nuevo algoritmo de factorización ha tomado el relevo de la criba cuadrática: la criba general de campo numérico. En 1989 los matemáticos te hubiesen dicho que la criba general de campo numérico nunca sería práctica. En 1992 te hubiesen dicho que era práctica, pero sólo más rápida que la criba cuadrática para números mayores que unos 130-150 dígitos. Hoy se sabe que es más ráipda que la criba cuadrática para números bien por debajo de 116 dígitos. La criba general de campo numérico puede factorizar un número de 512 bits más de 10 veces más rápido que la criba cuadrática. El algoritmo necesitaría menos de un año en un Intel Paragon de 1800 nodos. La Tabla 2 da el número de mips-año necesarios para factorizar números de diferentes tamaños, dadas las implementaciones actuales de la criba general de campo numérico.
Tabla 2: Factorización usando la criba general de campo numérico
Nº de bits
|
mips-año necesarios
|
512
|
30.000
|
768
|
2*10^8
|
1024
|
3*10^11
|
1280
|
1*10^14
|
1536
|
3*10^16
|
2048
|
3*10^20
|
Y la criba general de campo numérico aún se está haciendo más veloz. Los matemáticos siguen saliendo con nuevos trucos, nuevas optimizaciones, nuevas técnicas. No hay razón para pensar que esta tendencia no continuará. Un algoritmo relacionado, la criba especial de campo numérico, ya puede factorizar números de una cierta forma - números no usados habitualmente en criptografía - mucho más rápidamente que la criba general de campo numérico para números del mismo tamaño. No es irrazonable suponer que la criba general de campo numérico pueda ser optimizada para correr igual de rápido; es posible que la NSA [Agencia de Seguridad Nacional] ya sepa hacerlo. La Tabla 3 da el número de mips-año requeridos para que esta criba especial de campo numérico factorice números de distintas longitudes.
Tabla 3: Factorización usando la criba especial de campo numérico
Nº de bits
|
mips-año necesarios
|
512
|
< 200
|
768
|
100.000
|
1024
|
3*10^7
|
1280
|
3*10^9
|
1536
|
2*10^11
|
2048
|
4*10^14
|
En un "workshop" [reunión de trabajo] del Instituto Europeo de Seguridad en Sistemas, en 1992, los participantes estuvieron de acuerdo en que un módulo de 1024 bits sería suficiente para seguridad a largo plazo hasta el 2002. Sin embargo, advirtieron: "Aunque los participantes de esta reunión se sienten cualificados en sus áreas respectivas, esta declaración (respecto a la seguridad duradera) debe tomarse con precaución." Este es un buen consejo.
El criptógrafo sabio es ultraconservador cuando elige longitudes de claves públicas. Para determinar durante qué longitud de clave necesita, se mira tanto a la seguridad y vida útil pretendida para la clave como al estado de la tecnología de la factorización. Hoy se necesita un número de 1024 bits para obtener el nivel de seguridad que se tenía con una clave de 512 bits a principios de los ochenta. Si quieres que tus claves permanezcan seguras durante 20 años, 1024 bits es probablemente demasiado poco.
Incluso si tus secretos particulares no valen el esfuerzo necesario para factorizar tu módulo, puedes estar en peligro. Imagina un sistema de banca automatizado que use RSA para su seguridad. Mallory puede aparecer en el juicio y decir: "¿Leyó vd. en el periódico, en 1994, que se rompió RSA-129, y que los números de 512 bits pueden ser factorizados por cualquier organización que pueda gastarse unos cuantos millones de dólares y esperar unos meses? Mi banco usa números de 512 bits para su seguridad, y por cierto, yo no hice esas siete transferencias." Incluso si Mallory miente, el juez probablemente exigirá que el banco lo demuestre.
Antes, dije que hacer predicciones era una tontería. Ahora voy a hacer algunas. La Tabla 3 da mis recomendaciones para longitudes de claves públicas, dependiendo de durante cuánto tiempo necesitas que sea segura. Hay tres longitudes de clave para cada año: una segura contra un individuo, una segura contra una gran corporación, y la tercera segura contra un gran gobierno.
La criba especial del cuerpo de números (en inglés special number field sieve, SNFS) es un algoritmo especializado de factorización de números enteros. La criba (general) del cuerpo de números (GNFS) es una versión generalizada de este algoritmo que trata con números de todo tipo.
La criba especial de cuerpo de números es eficaz para los números de la forma  , donde
, donde  y
y  son pequeños. Se recomienda pues especialmente para descomponer en factores los números de Fermat y los números de Mersenne. NFSNET utilizó la SNFS mucho y de otros para descomponer en factores los números del proyecto de Cunningham.
son pequeños. Se recomienda pues especialmente para descomponer en factores los números de Fermat y los números de Mersenne. NFSNET utilizó la SNFS mucho y de otros para descomponer en factores los números del proyecto de Cunningham.
 , donde
, donde  y
y  son pequeños. Se recomienda pues especialmente para descomponer en factores los números de Fermat y los números de Mersenne. NFSNET utilizó la SNFS mucho y de otros para descomponer en factores los números del proyecto de Cunningham.
son pequeños. Se recomienda pues especialmente para descomponer en factores los números de Fermat y los números de Mersenne. NFSNET utilizó la SNFS mucho y de otros para descomponer en factores los números del proyecto de Cunningham.
la criba general del cuerpo de números (del inglés general number field sieve (GNFS) es el más eficientealgoritmo clásico conocido para factorizar enteros mayores de 100 dígitos. Heurísticamente, su complejidad para factorizar un entero n(consistente en log2 n bits) es de la forma
(en notación L), donde ln es el logaritmo en base e.1 Es una generalización de la criba especial del cuerpo de números: mientras que el último puede factorizar únicamente números de una cierta forma especial, la criba general del cuerpo de números puede factorizar cualquier número aparte de potencias primas (que es trivial factorizar tomando raíces). Cuando el término en inglés number field sieve(NFS) es usado sin calificación, este se refiere a la criba general del cuerpo de números.
El principio de la criba del cuerpo de números (ambas, especial y general) se puede entender como una mejora de la más simple criba racional o criba cuadrática. Cuando se usan tales algoritmos para factorizar un número grande n, es necesaria la búsqueda de números lisos (i.e. números con factores primos pequeños) de orden n1/2. El tamaño de esos valores es exponencial en el tamaño de n (véase después). La criba general del cuerpo de números, por otra parte, gestiona la búsqueda de números lisos que sean subexponenciales en el tamaño de n. Puesto que esos números son más pequeños, son más propensos a ser lisos que los números evaludados en los algoritmos anteriores. Esta es la clave de la eficiencia de la criba del cuerpo de números. Con el fin de lograr esta aceleración, la criba del cuerpo de números tiene que realizar los cálculos y factorizaciones en cuerpos numéricos. Esto resulta en muchos aspectos lo más complicado del algoritmo, si lo comparamos con la más simple criba racional.
Nótese que log2 n es el número de bits en la representación binaria del n, que es el tamaño de la entrada para el algoritmo, así que cualquier elemento de orden nc para una constante c es exponencial en log n. El tiempo de ejecución de la la criba del cuerpo de números es super-polinomial pero sub-exponencial en el tamaño de la entrada.
criba racional es un algoritmo general para la factorizar enteros en factores primos. Es esencialmente un caso especial de la criba general del cuerpo de números, y mientras que es mucho menos eficiente que el algoritmo general, es conceptualmente más simple. Así que, mientras es más bien un algoritmo de factorización sin utilidad en la práctica, es de utilidad como primer paso para aquellos que tratan de entender cómo funciona la criba general de cuerpo de números.
Método
Suponga que intenta factorizar el número compuesto n. Se puede elegir una acotación B, e identificar el factor base (que se llamará P), al conjunto de todos los primos menores o iguales a B. A continuación, se buscan los enteros positivos z tales que tanto z y z + n sean B-liso — i.e. todos sus factores primos están en P. Por tanto, podemos escribir, para los exponentes adecuados  ,
,
 ,
,
y del mismo modo, para el adecuado 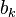 , tenemos
, tenemos
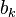 , tenemos
, tenemos .
.
Pero  y
y  son congruentes módulo
son congruentes módulo  , y por lo que cada número entero tal z que encontramos con dé una relación multiplicativa (mod n) entre los elementos deP, i.e.
, y por lo que cada número entero tal z que encontramos con dé una relación multiplicativa (mod n) entre los elementos deP, i.e.
 y
y  son congruentes módulo
son congruentes módulo  , y por lo que cada número entero tal z que encontramos con dé una relación multiplicativa (mod n) entre los elementos deP, i.e.
, y por lo que cada número entero tal z que encontramos con dé una relación multiplicativa (mod n) entre los elementos deP, i.e.
(donde los ai y bi son enteros no negativos.)
Cuando se hayan generado las suficientes de estas relaciones (por lo general es suficiente con que el número de relaciones sea un poco más que el tamaño de P), podemos utilizar los métodos del álgebra lineal para multiplicarlos junto a estas varias relaciones de manera que los exponentes de los números primos sean todos pares. Entonces se obtendrá una congruencia de cuadrados de la forma a2≡b2 (mod n), que puede convertirse en una factorización de n, n = mcd(a-b,n)×mcd(a+b,n). Esta factorización podría llegar a ser trivial (i.e. n=n×1), en cuyo caso tenemos que intentarlo de nuevo con una combinación diferente de las relaciones; pero con suerte tendremos un par no trivial de los factores de n, y el algoritmo terminará.
Ejemplo
Factorizaremos el entero n = 187 usando la criba racional. Tomaremos arbitrariamente el valor B=7, obteniendo el factor base P = {2,3,5,7}. El primer paso es comprobar la divisibilidad de cada uno de los miembros de P en n; claramente si n es divisible por uno de esos primos, entonces habremos finalizado ya. Sin embargo, 187 no es divisible por 2, 3, 5, o 7. Seguidamente, buscamos los valores adecuados de z; los primeros son 2, 5, 9, y 56. Los cuatro valores adecuados de z dan cuatro relaciones multiplicativas (mod 187):
- 21305070 = 2 ≡ 189 = 20335071.............(1)
- 20305170 = 5 ≡ 192 = 26315070.............(2)
- 20325070 = 9 ≡ 196 = 22305072.............(3)
- 23305071 = 56 ≡ 243 = 20355070.............(4)
Ahora hay esencialmente varias maneras diferentes de combinar estos y acabar con exponentes pares. Por ejemplo,
- (1)×(4): Después de multiplicarlos y, anulando el factor común de 7 (lo cual podemos hacer puesto que 7 se considera un miembro de P, y se ha determinado que estos son coprimos con n1 ), esto se reduce a 24 ≡ 38, o 42 ≡ 812. La factorización resultante es 187 = mcd(81-4,187) × mcd(81+4,187) = 11×17.
Alternativamente, la ecuación (3) está en la forma adecuada ya:
- (3): Esto dice que 32 ≡ 142 (mod n), que proporciona la factorización 187 = mcd(14-3,187) × mcd(14+3,187) = 11×17.
Limitaciones del algoritmo
La criba racional, como la criba general del cuerpo de números, no puede factorizar números de la forma pm, donde p es un primo y m es un entero. Esto no es un gran problema, dado que tales números son estadísticamente raros, y más aún, hay un proceso simple y rápido para verificar si un número dado es de esta forma. Probablemente el método más elegante es verificar si  se cumple para cualquier 1 < b < log(n) usando una versión entera del método de Newton para la extracción de raíces.2
se cumple para cualquier 1 < b < log(n) usando una versión entera del método de Newton para la extracción de raíces.2
 se cumple para cualquier 1 < b < log(n) usando una versión entera del método de Newton para la extracción de raíces.2
se cumple para cualquier 1 < b < log(n) usando una versión entera del método de Newton para la extracción de raíces.2
El mayor problema es encontrar un número suficiente de z tales que para ambos, z y z+n, sean B-lisos. Para cualquier B dado, las proporción de números que son B-lisos decrece rápidamente con el tamaño del número. Así que si n es grande (digamos, un centenar de dígitos), será difícil o imposible encontrar los suficientes z para que el algoritmo funcione. La ventaja de la criba general del cuerpo de números es que se necesita únicamente buscar números lismo del orden de n1/d para algún entero positivo d (típicamente 3 o 5), a diferencia del orden n que es requerido aquí.

![\exp\left( \left(\sqrt[3]{\frac{64}{9}} + o(1)\right)(\ln n)^{\frac{1}{3}}(\ln \ln n)^{\frac{2}{3}}\right) =L_n\left[\frac{1}{3},\sqrt[3]{\frac{64}{9}}\right]](https://upload.wikimedia.org/math/2/9/6/296c15df549eb239cdcffd4defb7496a.png)


No hay comentarios:
Publicar un comentario