Algoritmos de clasificación
máquinas de soporte vectorial o máquinas de vectores de soporte (Support Vector Machines, SVMs) son un conjunto de algoritmos de aprendizaje supervisado desarrollados por Vladimir Vapnik y su equipo en los laboratorios AT&T.
Estos métodos están propiamente relacionados con problemas de clasificación y regresión. Dado un conjunto de ejemplos de entrenamiento (de muestras) podemos etiquetar las clases y entrenar una SVM para construir un modelo que prediga la clase de una nueva muestra. Intuitivamente, una SVM es un modelo que representa a los puntos de muestra en el espacio, separando las clases por un espacio lo más amplio posible. Cuando las nuevas muestras se ponen en correspondencia con dicho modelo, en función de su proximidad pueden ser clasificadas a una u otra clase.
Más formalmente, una SVM construye un hiperplano o conjunto de hiperplanos en un espacio de dimensionalidad muy alta (o incluso infinita) que puede ser utilizado en problemas de clasificación o regresión. Una buena separación entre las clases permitirá un clasificación correcta.
Idea básica
Dado un conjunto de puntos, subconjunto de un conjunto mayor (espacio), en el que cada uno de ellos pertenece a una de dos posibles categorías, un algoritmo basado en SVM construye un modelo capaz de predecir si un punto nuevo (cuya categoría desconocemos) pertenece a una categoría o a la otra.
Como en la mayoría de los métodos de clasificación supervisada, los datos de entrada (los puntos) son vistos como un vector p-dimensional (una lista de p números).
La SVM busca un hiperplano que separe de forma óptima a los puntos de una clase de la de otra, que eventualmente han podido ser previamente proyectados a un espacio de dimensionalidad superior.
En ese concepto de "separación óptima" es donde reside la característica fundamental de las SVM: este tipo de algoritmos buscan el hiperplano que tenga la máxima distancia (margen) con los puntos que estén más cerca de él mismo. Por eso también a veces se les conoce a las SVM como clasificadores de margen máximo. De esta forma, los puntos del vector que son etiquetados con una categoría estarán a un lado del hiperplano y los casos que se encuentren en la otra categoría estarán al otro lado.
Los algoritmos SVM pertenecen a la familia de los clasificadores lineales. También pueden ser considerados un caso especial de la regularización de Tikhonov.
En la literatura de los SVMs, se llama atributo a la variable predictora y característica a un atributo transformado que es usado para definir el hiperplano. La elección de la representación más adecuada del universo estudiado, se realiza mediante un proceso denominado selección de características.
Al vector formado por los puntos más cercanos al hiperplano se le llama vector de soporte.
Los modelos basados en SVMs están estrechamente relacionados con las redes neuronales. Usando una función kernel, resultan un método de entrenamiento alternativo para clasificadores polinomiales, funciones de base radial y perceptrón multicapa.
Ejemplo en 2–dimensiones
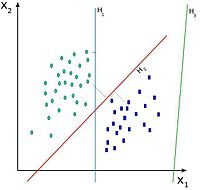
En el siguiente ejemplo idealizado para 2-dimensiones, la representación de los datos a clasificar se realiza en el plano x-y. El algoritmo SVM trata de encontrar un hiperplano 1-dimensional (en el ejemplo que nos ocupa es una línea) que une a las variables predictoras y constituye el límite que define si un elemento de entrada pertenece a una categoría o a la otra.
Existe un número infinito de posibles hiperplanos (líneas) que realicen la clasificación pero, ¿cuál es la mejor y cómo la definimos?
La mejor solución es aquella que permita un margen máximo entre los elementos de las dos categorías.
Se denominan vectores de soporte a los puntos que conforman las dos líneas paralelas al hiperplano, siendo la distancia entre ellas (margen) la mayor posible.
Soft margin: Errores de entrenamiento
Idealmente, el modelo basado en SVM debería producir un hiperplano que separe completamente los datos del universo estudiado en dos categorías. Sin embargo, una separación perfecta no siempre es posible y, si lo es, el resultado del modelo no puede ser generalizado para otros datos. Esto se conoce como sobreajuste (overfitting).
Con el fin de permitir cierta flexibilidad, los SVM manejan un parámetro C que controla la compensación entre errores de entrenamiento y los márgenes rígidos, creando así un margen blando (soft margin) que permita algunos errores en la clasificación a la vez que los penaliza.
Función Kernel
La manera más simple de realizar la separación es mediante una línea recta, un plano recto o un hiperplano N-dimensional.
Desafortunadamente los universos a estudiar no se suelen presentar en casos idílicos de dos dimensiones como en el ejemplo anterior, sino que un algoritmo SVM debe tratar con a) más de dos variables predictoras, b) curvas no lineales de separación, c) casos donde los conjuntos de datos no pueden ser completamente separados, d) clasificaciones en más de dos categorías.
Debido a las limitaciones computacionales de las máquinas de aprendizaje lineal, éstas no pueden ser utilizadas en la mayoría de las aplicaciones del mundo real. La representación por medio de funciones Kernel ofrece una solución a este problema, proyectando la información a un espacio de características de mayor dimensión el cual aumenta la capacidad computacional de la máquinas de aprendizaje lineal. Es decir, mapearemos el espacio de entradas X a un nuevo espacio de características de mayor dimensionalidad (Hilbert):
-
-
- F = {φ(x)|x ∈ X}
-
-
-
-
- x = {x1, x2, · · ·, xn} → φ(x) = {φ(x)1, φ(x)2, · · ·, φ(x)n}
-
-
Tipos de funciones Kernel (Núcleo)
- Polinomial-homogénea: K(xi, xj) = (xi·xj)n
- Perceptron: K(xi, xj)= || xi-xj ||
- Función de base radial Gaussiana: separado por un hiperplano en el espacio transformado.
-
-
- K(xi, xj)=exp(-(xi-xj)2/2(sigma)2)
-
- Sigmoid: K(xi, xj)=tanh(xi· xj−θ)
SVR. Regresión
Una nueva versión de SVM para regresión fue propuesta en 1996 por Vladimir Vapnik, Harris Drucker, Chris Burges, Linda Kaufman y Alex Smola.[nota].
La idea básica de SVR consiste en realizar un mapeo de los datos de entrenamiento x ∈ X, a un espacio de mayor dimensión F a través de un mapeo no lineal φ: X → F, donde podemos realizar una regresión lineal.
SVM Multiclase
Hay dos filosofías básicas para resolver el problema de querer clasificar los datos en más de dos categorías:
- a) cada categoría es dividida en otras y todas son combinadas.
- b) se construyen k(k-1) / 2 modelos donde k es el número de categorías.
El perceptrón dentro del campo de las redes neuronales tiene dos acepciones. Puede referirse a un tipo de red neuronal artificial desarrollado por Frank Rosenblatt. Y dentro de la misma teoría de Rosenblatt, también puede entenderse como la neurona artificial y unidad básica de inferencia en forma de discriminador lineal, es decir, un algoritmo capaz de generar un criterio para seleccionar un sub-grupo, de un grupo de componentes más grande. La limitación de este algoritmo es que si dibujamos en un plot estos elementos, se deben poder separar con un hiperplano los elementos "deseados" de los "no deseados". El perceptrón puede utilizarse con otros perceptrones u otro tipo de neurona artificial, para formar redes neuronales más complicadas.
Definición
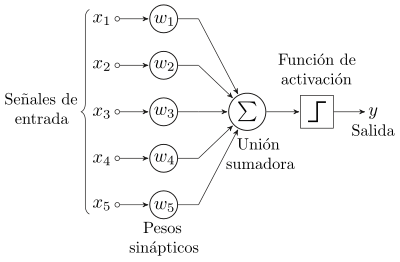
El modelo biológico más simple de un perceptrón es una neurona y viceversa. Es decir, el modelo matemático más simple de una neurona es un perceptrón. La neuronaes una célula especializada y caracterizada por poseer una cantidad indefinida de canales de entrada llamados dendritas y un canal de salida llamado axón. Las dendritas operan como sensores que recogen información de la región donde se hallan y la derivan hacia el cuerpo de la neurona que reacciona mediante una sinapsis que envía una respuesta hacia el cerebro, esto en el caso de los seres vivos.
Una neurona sola y aislada carece de razón de ser. Su labor especializada se torna valiosa en la medida en que se asocia a otras neuronas, formando una red. Normalmente, el axón de una neurona entrega su información como "señal de entrada" a una dendrita de otra neurona y así sucesivamente. El perceptrón que capta la señal en adelante se entiende formando una red de neuronas, sean éstas biológicas o de sustrato semiconductor (compuertas lógicas).
El perceptrón usa una matriz para representar las redes neuronales y es un discriminador terciario que traza su entrada  (un vector binario) a un único valor de salida
(un vector binario) a un único valor de salida  (un solo valor binario) a través de dicha matriz.
(un solo valor binario) a través de dicha matriz.
 (un vector binario) a un único valor de salida
(un vector binario) a un único valor de salida  (un solo valor binario) a través de dicha matriz.
(un solo valor binario) a través de dicha matriz.
Donde  es un vector de pesos reales y
es un vector de pesos reales y 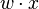 es el producto escalar (que computa una suma ponderada).
es el producto escalar (que computa una suma ponderada).  es el 'umbral', el cual representa el grado de inhibición de la neurona, es un término constante que no depende del valor que tome la entrada.
es el 'umbral', el cual representa el grado de inhibición de la neurona, es un término constante que no depende del valor que tome la entrada.
 es un vector de pesos reales y
es un vector de pesos reales y 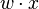 es el producto escalar (que computa una suma ponderada).
es el producto escalar (que computa una suma ponderada).  es el 'umbral', el cual representa el grado de inhibición de la neurona, es un término constante que no depende del valor que tome la entrada.
es el 'umbral', el cual representa el grado de inhibición de la neurona, es un término constante que no depende del valor que tome la entrada.
El valor de  (0 o 1) se usa para clasificar
(0 o 1) se usa para clasificar  como un caso positivo o un caso negativo, en el caso de un problema de clasificación binario. El umbral puede pensarse de como compensar la función de activación, o dando un nivel bajo de actividad a la neurona del rendimiento. La suma ponderada de las entradas debe producir un valor mayor que
como un caso positivo o un caso negativo, en el caso de un problema de clasificación binario. El umbral puede pensarse de como compensar la función de activación, o dando un nivel bajo de actividad a la neurona del rendimiento. La suma ponderada de las entradas debe producir un valor mayor que  para cambiar la neurona de estado 0 a 1.
para cambiar la neurona de estado 0 a 1.
 (0 o 1) se usa para clasificar
(0 o 1) se usa para clasificar  como un caso positivo o un caso negativo, en el caso de un problema de clasificación binario. El umbral puede pensarse de como compensar la función de activación, o dando un nivel bajo de actividad a la neurona del rendimiento. La suma ponderada de las entradas debe producir un valor mayor que
como un caso positivo o un caso negativo, en el caso de un problema de clasificación binario. El umbral puede pensarse de como compensar la función de activación, o dando un nivel bajo de actividad a la neurona del rendimiento. La suma ponderada de las entradas debe producir un valor mayor que  para cambiar la neurona de estado 0 a 1.
para cambiar la neurona de estado 0 a 1.Aprendizaje
En el perceptrón, existen dos tipos de aprendizaje, el primero utiliza una tasa de aprendizaje mientras que el segundo no la utiliza. Esta tasa de aprendizaje amortigua el cambio de los valores de los pesos.1
El algoritmo de aprendizaje es el mismo para todas las neuronas, todo lo que sigue se aplica a una sola neurona en el aislamiento. Se definen algunas variables primero:
- el
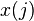 denota el elemento en la posición
denota el elemento en la posición  en el vector de la entrada
en el vector de la entrada - el
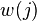 el elemento en la posición
el elemento en la posición  en el vector de peso
en el vector de peso - el
 denota la salida de la neurona
denota la salida de la neurona - el
 denota la salida esperada
denota la salida esperada - el
 es una constante tal que
es una constante tal que 
Los dos tipos de aprendizaje difieren en este paso. Para el primer tipo de aprendizaje, utilizando tasa de aprendizaje, utilizaremos la siguiente regla de actualización de los pesos:
Para el segundo tipo de aprendizaje, sin utilizar tasa de aprendizaje, la regla de actualización de los pesos será la siguiente:
Por lo cual, el aprendizaje es modelado como la actualización del vector de peso después de cada iteración, lo cual sólo tendrá lugar si la salida  difiere de la salida deseada
difiere de la salida deseada  . Para considerar una neurona al interactuar en múltiples iteraciones debemos definir algunas variables más:
. Para considerar una neurona al interactuar en múltiples iteraciones debemos definir algunas variables más:
 difiere de la salida deseada
difiere de la salida deseada  . Para considerar una neurona al interactuar en múltiples iteraciones debemos definir algunas variables más:
. Para considerar una neurona al interactuar en múltiples iteraciones debemos definir algunas variables más: denota el vector de entrada para la iteración i
denota el vector de entrada para la iteración i denota el vector de peso para la iteración i
denota el vector de peso para la iteración i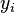 denota la salida para la iteración i
denota la salida para la iteración i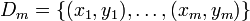 denota un periodo de aprendizaje de
denota un periodo de aprendizaje de  iteraciones
iteraciones
En cada iteración el vector de peso es actualizado como sigue:
- Para cada pareja ordenada
 en
en 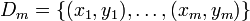
- Pasar
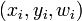 a la regla de actualización
a la regla de actualización 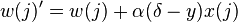
El periodo de aprendizaje  se dice que es separable linealmente si existe un valor positivo
se dice que es separable linealmente si existe un valor positivo  y un vector de peso
y un vector de peso  tal que:
tal que: 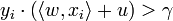 para todos los
para todos los  .
.
 se dice que es separable linealmente si existe un valor positivo
se dice que es separable linealmente si existe un valor positivo  y un vector de peso
y un vector de peso  tal que:
tal que: 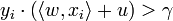 para todos los
para todos los  .
.
Novikoff (1962) probo que el algoritmo de aprendizaje converge después de un número finito de iteraciones si los datos son separables linealmente y el número de errores está limitado a: 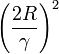 .
.
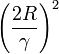 .
.
Sin embargo si los datos no son separables linealmente, la línea de algoritmo anterior no se garantiza que converja.
Ejemplo
Considere las funciones AND y OR, estas funciones son linealmente separables y por lo tanto pueden ser aprendidas por un perceptrón.
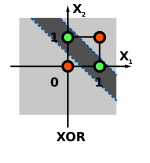
La función XOR no puede ser aprendida por un único perceptrón puesto que requiere al menos de dos líneas para separar las clases (0 y 1). Debe utilizarse al menos una capa adicional de perceptrones para permitir su aprendizaje.
Un perceptrón aprende a realizar la función binaria NAND con entradas  y
y  . Entradas:
. Entradas: 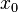 ,
,  ,
,  , donde
, donde 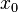 se mantiene constante en 1.
se mantiene constante en 1.
 y
y  . Entradas:
. Entradas: 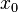 ,
,  ,
,  , donde
, donde 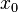 se mantiene constante en 1.
se mantiene constante en 1.
Umbral( ): 0.5
): 0.5
 ): 0.5
): 0.5
Bias ( ): 0
): 0
 ): 0
): 0
Taza de aprendizaje ( ): 0.1
): 0.1
 ): 0.1
): 0.1
Conjunto de entrenamiento, que consiste en cuatro muestras: 

En lo que sigue, los pesos finales de una iteración se convierten en los pesos iniciales de la siguiente. Cada ciclo sobre todas las muestras en el conjunto de entrenamiento está marcado con líneas gruesas.
| Entrada | Pesos iniciales | Salida | Error | Corrección | Pesos finales | |||||||||||
| Valores de sensor | Salida deseada | Sensor | Suma | Red | ||||||||||||
 |  |  |  |  |  | 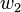 | 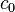 |  |  |  |  |  |  |  |  | 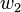 |
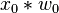 |  |  |  | if  then 1, else 0 then 1, else 0 |  |  |  |  | 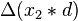 | |||||||
| 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | +0.1 | 0.1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0.1 | 0 | 0 | 0.1 | 0 | 0 | 0.1 | 0 | 1 | +0.1 | 0.2 | 0 | 0.1 |
| 1 | 1 | 0 | 1 | 0.2 | 0 | 0.1 | 0.2 | 0 | 0 | 0.2 | 0 | 1 | +0.1 | 0.3 | 0.1 | 0.1 |
| 1 | 1 | 1 | 0 | 0.3 | 0.1 | 0.1 | 0.3 | 0.1 | 0.1 | 0.5 | 0 | 0 | 0 | 0.3 | 0.1 | 0.1 |
| 1 | 0 | 0 | 1 | 0.3 | 0.1 | 0.1 | 0.3 | 0 | 0 | 0.3 | 0 | 1 | +0.1 | 0.4 | 0.1 | 0.1 |
| 1 | 0 | 1 | 1 | 0.4 | 0.1 | 0.1 | 0.4 | 0 | 0.1 | 0.5 | 0 | 1 | +0.1 | 0.5 | 0.1 | 0.2 |
| 1 | 1 | 0 | 1 | 0.5 | 0.1 | 0.2 | 0.5 | 0.1 | 0 | 0.6 | 1 | 0 | 0 | 0.5 | 0.1 | 0.2 |
| 1 | 1 | 1 | 0 | 0.5 | 0.1 | 0.2 | 0.5 | 0.1 | 0.2 | 0.8 | 1 | -1 | -0.1 | 0.4 | 0 | 0.1 |
| 1 | 0 | 0 | 1 | 0.4 | 0 | 0.1 | 0.4 | 0 | 0 | 0.4 | 0 | 1 | +0.1 | 0.5 | 0 | 0.1 |
| 1 | 0 | 1 | 1 | 0.5 | 0 | 0.1 | 0.5 | 0 | 0.1 | 0.6 | 1 | 0 | 0 | 0.5 | 0 | 0.1 |
| 1 | 1 | 0 | 1 | 0.5 | 0 | 0.1 | 0.5 | 0 | 0 | 0.5 | 0 | 1 | +0.1 | 0.6 | 0.1 | 0.1 |
| 1 | 1 | 1 | 0 | 0.6 | 0.1 | 0.1 | 0.6 | 0.1 | 0.1 | 0.8 | 1 | -1 | -0.1 | 0.5 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0.5 | 0 | 0 | 0.5 | 0 | 0 | 0.5 | 0 | 1 | +0.1 | 0.6 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0.6 | 0 | 0 | 0.6 | 0 | 0 | 0.6 | 1 | 0 | 0 | 0.6 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0.6 | 0 | 0 | 0.6 | 0 | 0 | 0.6 | 1 | 0 | 0 | 0.6 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0.6 | 0 | 0 | 0.6 | 0 | 0 | 0.6 | 1 | -1 | -0.1 | 0.5 | -0.1 | -0.1 |
| 1 | 0 | 0 | 1 | 0.5 | -0.1 | -0.1 | 0.5 | 0 | 0 | 0.5 | 0 | 1 | +0.1 | 0.6 | -0.1 | -0.1 |
| 1 | 0 | 1 | 1 | 0.6 | -0.1 | -0.1 | 0.6 | 0 | -0.1 | 0.5 | 0 | 1 | +0.1 | 0.7 | -0.1 | 0 |
| 1 | 1 | 0 | 1 | 0.7 | -0.1 | 0 | 0.7 | -0.1 | 0 | 0.6 | 1 | 0 | 0 | 0.7 | -0.1 | 0 |
| 1 | 1 | 1 | 0 | 0.7 | -0.1 | 0 | 0.7 | -0.1 | 0 | 0.6 | 1 | -1 | -0.1 | 0.6 | -0.2 | -0.1 |
| 1 | 0 | 0 | 1 | 0.6 | -0.2 | -0.1 | 0.6 | 0 | 0 | 0.6 | 1 | 0 | 0 | 0.6 | -0.2 | -0.1 |
| 1 | 0 | 1 | 1 | 0.6 | -0.2 | -0.1 | 0.6 | 0 | -0.1 | 0.5 | 0 | 1 | +0.1 | 0.7 | -0.2 | 0 |
| 1 | 1 | 0 | 1 | 0.7 | -0.2 | 0 | 0.7 | -0.2 | 0 | 0.5 | 0 | 1 | +0.1 | 0.8 | -0.1 | 0 |
| 1 | 1 | 1 | 0 | 0.8 | -0.1 | 0 | 0.8 | -0.1 | 0 | 0.7 | 1 | -1 | -0.1 | 0.7 | -0.2 | -0.1 |
| 1 | 0 | 0 | 1 | 0.7 | -0.2 | -0.1 | 0.7 | 0 | 0 | 0.7 | 1 | 0 | 0 | 0.7 | -0.2 | -0.1 |
| 1 | 0 | 1 | 1 | 0.7 | -0.2 | -0.1 | 0.7 | 0 | -0.1 | 0.6 | 1 | 0 | 0 | 0.7 | -0.2 | -0.1 |
| 1 | 1 | 0 | 1 | 0.7 | -0.2 | -0.1 | 0.7 | -0.2 | 0 | 0.5 | 0 | 1 | +0.1 | 0.8 | -0.1 | -0.1 |
| 1 | 1 | 1 | 0 | 0.8 | -0.1 | -0.1 | 0.8 | -0.1 | -0.1 | 0.6 | 1 | -1 | -0.1 | 0.7 | -0.2 | -0.2 |
| 1 | 0 | 0 | 1 | 0.7 | -0.2 | -0.2 | 0.7 | 0 | 0 | 0.7 | 1 | 0 | 0 | 0.7 | -0.2 | -0.2 |
| 1 | 0 | 1 | 1 | 0.7 | -0.2 | -0.2 | 0.7 | 0 | -0.2 | 0.5 | 0 | 1 | +0.1 | 0.8 | -0.2 | -0.1 |
| 1 | 1 | 0 | 1 | 0.8 | -0.2 | -0.1 | 0.8 | -0.2 | 0 | 0.6 | 1 | 0 | 0 | 0.8 | -0.2 | -0.1 |
| 1 | 1 | 1 | 0 | 0.8 | -0.2 | -0.1 | 0.8 | -0.2 | -0.1 | 0.5 | 0 | 0 | 0 | 0.8 | -0.2 | -0.1 |
| 1 | 0 | 0 | 1 | 0.8 | -0.2 | -0.1 | 0.8 | 0 | 0 | 0.8 | 1 | 0 | 0 | 0.8 | -0.2 | -0.1 |
| 1 | 0 | 1 | 1 | 0.8 | -0.2 | -0.1 | 0.8 | 0 | -0.1 | 0.7 | 1 | 0 | 0 | 0.8 | -0.2 | -0.1 |
Este ejemplo se puede implementar en el siguiente código en Python.




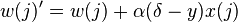
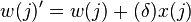


No hay comentarios:
Publicar un comentario