Configuración electrónica
Un orbital atómico es una determinada solución particular, espacial e independiente del tiempo, a laecuación de Schrödinger para el caso de un electrón sometido a un potencial coulombiano. La elección de tres números cuánticos en la solución general señalan unívocamente a un estado monoelectrónico posible.
Estos tres números cuánticos hacen referencia a la energía total del electrón, el momento angular orbital y la proyección del mismo sobre el eje z del sistema del laboratorio y se denotan por
Un orbital también puede representar la posición independiente del tiempo de un electrón en una molécula, en cuyo caso se denomina orbital molecular.
La combinación de todos los orbitales atómicos dan lugar a la corteza electrónica, representada por elmodelo de capas, el cual se ajusta a cada elemento químico según la configuración electrónicacorrespondiente.
Introducción
El orbital es la descripción ondulatoria del tamaño, forma y orientación de una región del espacio disponible para un electrón.1 Cada orbital con diferentes valores de npresenta una energía específica para el estado del electrón.
La posición (la probabilidad de la amplitud) de encontrar un electrón en un punto determinado del espacio se define mediante sus coordenadas en el espacio. Encoordenadas cartesianas dicha probabilidad se denota como  , donde
, donde  no se puede medir directamente.
no se puede medir directamente.
 , donde
, donde  no se puede medir directamente.
no se puede medir directamente.
Al suponer en los átomos simetría esférica, se suele trabajar con la función de onda en términos de coordenadas esféricas, 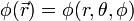 .
.
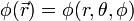 .
.Fundamentos físicos
La función de ondas
En el modelo atómico surgido tras la aplicación de la mecánica cuántica a la descripción de los electrones en los átomos (modelo posterior al modelo atómico de Bohr),2 se denomina orbital atómico a cada una de las funciones de onda monoelectrónicas que describen los estados estacionarios y espaciales de los átomos hidrogenoides. Es decir, son los estados físicos estacionarios en representación de posición,  , que se obtienen resolviendo la ecuación de Schrödinger independiente del tiempo
, que se obtienen resolviendo la ecuación de Schrödinger independiente del tiempo  , es decir, las funciones propias del operador hamiltoniano,
, es decir, las funciones propias del operador hamiltoniano, 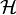 ).
).
 , que se obtienen resolviendo la ecuación de Schrödinger independiente del tiempo
, que se obtienen resolviendo la ecuación de Schrödinger independiente del tiempo  , es decir, las funciones propias del operador hamiltoniano,
, es decir, las funciones propias del operador hamiltoniano, 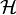 ).
).
No representan la posición concreta de un electrón en el espacio, que no puede conocerse dada su naturaleza mecanocuántica, sino que representan una región del espacio en torno al núcleo atómico en la que la probabilidad de encontrar al electrón es elevada (por lo que en ocasiones al orbital se le llama Región espacio energética de manifestación probabilística electrónica o REEMPE).
Los números cuánticos
En el caso del átomo de hidrógeno, se puede resolver la ecuación de Schrödinger de forma exacta, encontrando que las funciones de onda están determinadas por los valores de tres números cuánticos n, l, ml, es decir, dicha ecuación impone una serie de restricciones en el conjunto de soluciones que se identifican con una serie de números cuánticos. Estas condiciones surgen a través de las relaciones existentes entre estos números; no todos los valores son posibles físicamente.
- El valor del número cuántico n (número cuántico principal, toma valores 1,2,3...) define el tamaño del orbital. Cuanto mayor sea, mayor será el volumen. También es el que tiene mayor influencia en la energía del orbital.
- El valor del número cuántico l (número cuántico del momento angular) indica la forma del orbital y el momento angular. El momento angular viene dado por:
La notación (procedente de la espectroscopia) es la siguiente:
- Para l = 0, orbitales s
- Para l = 1, orbitales p
- Para l = 2, orbitales d
- Para l = 3, orbitales f
- Para l = 4, orbitales g; siguiéndose ya el orden alfabético.
El nombre que se asigna a las distintas clases de orbitales se debe a su relación con las líneas del espectro de un elemento (en inglés s sharp, p principal, d diffuse y ffundamental y el resto de los nombres, a partir de aquí, siguen el orden alfabético g, h ).
- El valor de ml (número cuántico magnético) define la orientación espacial del orbital frente a un campo magnético externo. Para la proyección del momento angular frente al campo externo, se verifica:
Posteriormente se tuvo la necesidad de incluir ad hoc el espín del electrón, el cual viene descrito por otros dos números cuánticos s y ms. En la mecánica cuántica relativista el espín surge de forma espontánea y no hace falta introducirlo a mano.
- El valor de s (número cuántico de espín) para el electrón es 1/2, mientras que ms puede tomar los valores +1/2 ó -1/2 (cuando no se tiene en cuenta el espín se dice que el orbital es un orbital espacial mientras que si se considera el espín, se denomina espín orbital).
La función de onda se puede descomponer, empleando como sistema de coordenadas las coordenadas esféricas, de la siguiente forma:
donde  representa la parte del orbital que depende de la distancia del electrón al núcleo y
representa la parte del orbital que depende de la distancia del electrón al núcleo y  es la parte que depende de los ángulos (geometría sobre una esfera unidad) del orbital y son los armónicos esféricos:
es la parte que depende de los ángulos (geometría sobre una esfera unidad) del orbital y son los armónicos esféricos:
 representa la parte del orbital que depende de la distancia del electrón al núcleo y
representa la parte del orbital que depende de la distancia del electrón al núcleo y  es la parte que depende de los ángulos (geometría sobre una esfera unidad) del orbital y son los armónicos esféricos:
es la parte que depende de los ángulos (geometría sobre una esfera unidad) del orbital y son los armónicos esféricos:
Para la representación gráfica del orbital se emplea la función cuadrado,  y
y 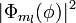 , ya que ésta es proporcional a la densidad de carga y por tanto a la densidad de probabilidad, es decir, el volumen que encierra la mayor parte de la probabilidad de encontrar al electrón o, si se prefiere, el volumen o región del espacio en la que el electrón pasa la mayor parte del tiempo.
, ya que ésta es proporcional a la densidad de carga y por tanto a la densidad de probabilidad, es decir, el volumen que encierra la mayor parte de la probabilidad de encontrar al electrón o, si se prefiere, el volumen o región del espacio en la que el electrón pasa la mayor parte del tiempo.
 y
y 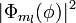 , ya que ésta es proporcional a la densidad de carga y por tanto a la densidad de probabilidad, es decir, el volumen que encierra la mayor parte de la probabilidad de encontrar al electrón o, si se prefiere, el volumen o región del espacio en la que el electrón pasa la mayor parte del tiempo.
, ya que ésta es proporcional a la densidad de carga y por tanto a la densidad de probabilidad, es decir, el volumen que encierra la mayor parte de la probabilidad de encontrar al electrón o, si se prefiere, el volumen o región del espacio en la que el electrón pasa la mayor parte del tiempo.Más allá del átomo de hidrógeno
En sentido estricto, los orbitales son construcciones matemáticas que tratan de describir, de forma coherente con la mecánica cuántica, los estados estacionarios de un electrón en un campo eléctrico de simetría central. (Dado que el núcleo no está descrito de forma explícita, ni siquiera describen de forma completa al átomo dehidrógeno).
Estas construcciones matemáticas no están preparadas, por su origen monoelectrónico, para tener en cuenta ni la correlación entre electrones ni la antisimetría exigida por la estadística de Fermi (los electrones son fermiones).
Sin embargo, saliéndose de su sentido estricto, han demostrado ser de enorme utilidad para los químicos, de forma que se utilizan no solo para sistemas polielectrónicos, sino también para sistemas polinucleares (como las moléculas). También, más allá de su sentido estricto, los químicos se refieren a ellos como entes físicos más que como construcciones matemáticas, con expresiones como «en un orbital caben dos electrones».[cita requerida]
Formas de los orbitales
Por simplicidad, se recogen las formas de la parte angular de los orbitales, obviando los nodos radiales, que siempre tienen forma esférica.
Orbital "s"
El orbital s tiene simetría esférica alrededor del núcleo atómico. En la figura siguiente se muestran dos formas alternativas para representar la nube electrónica de un orbital s: en la primera, la probabilidad de encontrar al electrón (representada por la densidad de puntos) disminuye a medida que nos alejamos del centro; en la segunda, se representa el volumen esférico en que el electrón pasa la mayor parte del tiempo y por último se observa el electrón.
Orbitales "p"
La forma geométrica de los orbitales p es la de dos esferas achatadas hacia el punto de contacto (el núcleo atómico) y orientadas según los ejes de coordenadas. En función de los valores que puede tomar el tercer número cuántico ml (-1, 0 y 1) se obtienen los tres orbitales p simétricos respecto a los ejes x, z e y. Análogamente al caso anterior, los orbitales p presentan n-2 nodos radiales en la densidad electrónica, de modo que al incrementarse el valor del número cuántico principal la probabilidad de encontrar el electrón se aleja del núcleo atómico. El orbital "p" representa también la energía que posee un electrón y se incrementa a medida que se aleja entre la distancia del núcleo y el orbital.
Orbitales "d"
Los orbitales d tienen formas más diversas. Cuatro de ellos tienen forma de 4 lóbulos de signos alternados (dos planos nodales, en diferentes orientaciones del espacio), y el último es un doble lóbulo rodeado por un anillo (un doble cono nodal). Siguiendo la misma tendencia, presentan n-3 nodos radiales. Este tiene 5 orbitales y corresponde al número cuántico l (azimutal)
Orbitales "f"
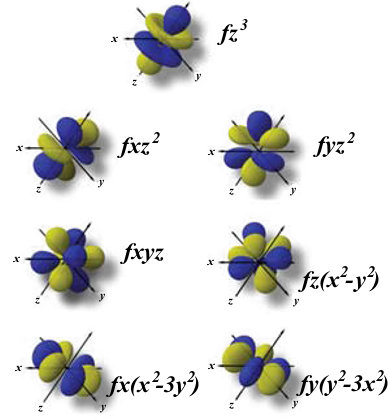
Los orbitales f tienen formas aún más exóticas, que se pueden derivar de añadir un plano nodal a las formas de los orbitales d. Presentan n-4 nodos radiales.
Tabla de orbitales
La tabla siguiente muestra todas las configuraciones orbitales para el hidrógeno, como funciones de onda, desde el 1s al 7s. Los átomos polielectrónicos irían alojando sus electrones en dichos grupos de orbitales.
Orbitales Atómicos
Estos números cuánticos sólo pueden tomar ciertos valores permitidos:
Los valores del número cuántico n indican el tamaño del orbital, es decir su cercanía al núcleo.
Los valores del número cuántico l definen el tipo de orbital:
• Si l= 0 el orbital es del tipo s
• Si l= 1 los orbitales son del tipo p
• Si l = 2 los orbitales son del tipo d
• Si l= 3 los orbitales son del tipo f
• principal : líneas intensas
• difuse : líneas difusas
• fundamental : líneas frecuentes en muchos espectros
![[1s]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_urRIUZv0kfMaIqbV5RhBUItIhj4bXOMeYdhczPaYO4eFtZSMEEBZjrPMqblrVhaR1K2Ayr_d4BHnFGdarcy6dcC642mSBZMeMKlKdfr23vD0tUcqfj-WZGZWQUe0Cfe77UR0vUjqZ4lA=s0-d)
![[2s]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_t_DtJy4FDo8YNe9uf4vC0AdcMbWleD0N_Tt0YpocSpdsYPonyoHz4j-t3Sjsu-JBeZh-iYpfOFk676cx6lv7852CqYfKASgYghnHD1XA4pwyWK2H6X7Uw2QeI4hIORSbwJGAjI2jsz=s0-d)
![[2px]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_tZajAcgRyf1e9dR5woBdzLw5H7qEqOtLr2Le6SI_dueLZ3JGqJJJrrhWt0GTSILm2J28qewAOWhR-LvDwMZtF26qUsJ2uSvSz-iqSJ8wEEO8ZIuRiJeTKG6gni219R5zEkUgCNz4EJIA=s0-d)
![[2py]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_vN02rsMLj5ToAH35OMp3ThBaY9nwAVLTTco2sQbDz8vF6NshV2LoUIyEi3lAoFfGN-V5paaJ9mMu73_ImeUaV2QStqJ6RWCo3H_FLC4AwrWcKun2b8qzxbxsuOkzvtNr0S8-89gp_ONA=s0-d)
![[2pz]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_tDVU-abQqnuSkZGftHG9HyRTOL7Vx5POYAllClN7UlN2G9sko5jbRQVkg3wWWz1bbi52wpqKR4kmbZk9tXHSvkVVQ_y1nKrl0UEcB3v8bAqC9hokwegzuC0-zyYXB60I3GCVuHgtb_7_Y=s0-d)
![[3s]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_tJhJ3q8kK5RCFyD1r1LRkuqZdHxmoBNgEGI2j9N2qsGH-GLb_8V_YERYlgEiqDbJZwgbWojFKXM2l5BVqwrxqgk9C1Z4bQEeG1zadl3TobfSza9oTA8jm82MJpoEn9iDxORrcSmd6Odg=s0-d)
si l = 1 tendremos los tres orbitales del tipo p:
![[3px]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_s-KPnI8N7SbGqPHCKxOKF7u9NtZ4O6vT3ycL59zCIY2ilTdTbjfa0H4BY6yhhGbZjhxBYAmUKVgYfwG8JnL44gYl0rwotReQUdXlxqq34kTdhR8T4YaSLNykwnhYrGgdMwKdjfeX-F7Q=s0-d)
![[3py]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_vOwBXUHlF29V6rl7kB1byGjwrQkDBehVgd_jOxENRchH3kNtERwwXkDjYrxECSXtMm0WDGoFOxWZQ5TFpBcQsuOva-pdrQYNi67-0mq3We53cV2Ca3Jxb-KSAwCOcMauHuYuO7JLdEwQ=s0-d)
![[3pz]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_s880kFpH476L5JQa2EHSZHSLy7LTQe7k8NeB6u5IsexqExW2DAHMwiAp_CNBqFIx0pF9XW0MYZqwD9F5UArHhgP6JvhOva2VxrHU5FHlxzc8yvXP1KKPrBk9CY4NlhvePEfNtlNFPxdQ=s0-d)
![[3dxy]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_v_yYF87_0M-IPc1zuGhaLf3HZSOAcl_Y_GYJ4jgOJHPounV_cAusdOIKFH9ANGb1sgKrENXDkIonig95x-3oUX1SnZpEwCRDTecTZSRETJp-HtsfcpNO7BBs2YV63f4adhzzr8t2mFr8bo=s0-d)
![[3dxz]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_tk42cP2SvmSB7HIHcWkIST_9FSK4bbpf2vGGDZxdISqkK85rsgpwAXXVjBUmSl2M8JcGgMUNujSDjoi06XJV9vPouzhltRXhfJkiTF32dnyGHu8kM4vivTAjiTwEqA-kv1tDAZKfznBoqz=s0-d)
![[3dyz]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_sGz3nzj12Bry3xhPZgbptEv6DW5UW90VZOtfYgmLTLakmsCsC9-1A1fCLVy-ruSQv5THmX15IyhIpcpfwREYFddb_MBa1R6xbUppalAUwURxsi6SmVhPje1qhLX1Cv3pdB-89wfa64oTqf=s0-d)
![[3dx2-y2]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_vDZEYWw3Q2o0sxPkw45_Y4Y7U9lMkWE5GGDUSgiZHphI7Gw_pNB7Uv9J1CbqQXZmIK5SUT0FCqVgZW4prI7TMU1lCAGqZHmn278kpl_sF3tIB8FapibhGC-fmALF_5amg2beRvZk7ywcufafYl=s0-d)
![[3dz2]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_s4ifeKZxlLoeB7TtvFlACfaUB3j0CANKgGivaA39IkTTWbUUb5XvlIWVNZZy9IwYOqyzIIfQyTh2arPxeRwwNZGIpMoXAL766uuQJ6vwDn2Ey32-wRYilfOo07Y-UOO5lfpxKjHVMclKA=s0-d)
Si n = 4, son posibles cuatro tipos de orbitales diferentes:
De tipo s (para l = 0):
![[4s]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_sV8UKHEumz5KnCdHf9gSiB1D_cgenk9dATgcnjEMRK-EO_suULzSRKgiATJS_isnCG3HTmag76sA2EIDgwNybXn0pUH4SbDBm3q_HhBAhMlR5zsUmZQzfF8cMDnN6yUd76DFievbnbmQ=s0-d)
De tipo p (para l = 1):
![[4px]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_uUZMdOQrK8f-ymjUmKFcZWz46v0t3QePNq6kjalM2f8wffrtmDEgvjAw42TZwShYWL-Lr0ewQluxPLQMghvosbYJqlwtkkDKBedSZsAHpLPq4n19-F_2-WlnwgV0qhV6yGcr2XakHJn_Y=s0-d)
![[4py]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_vq-iVO2_scbSDCD1n4GXQ2EbEUJehzIZw29ITmwrFtB11HlusvinuUH-NFCY0Dy3z5TZ6l0wORE1BJ-v_ZAKL_Sm2fYBn8WL-kaQem6FC1p4gQV9NxE8GzwtnWhWcBGq-bCSibnWI6n1I=s0-d)
![[4pz]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_uC5vmhrCvCRj-ixcR10RMz32AcwIccVoUHmxCGTQt-TW5YjQMYnUEm6Jgx4W9rAMMRVL3AuX4u6YNUYyIFe4Vtd4AHQ6AiDRRw_aHoe2eGKij1dQCsLvg5lZOrNlIc60i36EQxOWv-UOM=s0-d)
De tipo d (para l = 2):
![[4dxy]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_vhrypSpb-D08GjySGRzRiQAqGCxd3YHcCvsQSzSaY3UI0d3rfW3UhH7m82J80u5RljQim9CimHBb-tQSREzY-nXip_ri7wlSy1GLmDZ6c1PEfdS2QdgRcY_7UbKtfoLCgnAd0wR2O05q9Z=s0-d)
![[4dxz]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_uCiR4VFImj5e1oJhnlCuY-2MUjc_yI_bZaAgjJTsIhQEGNOIYb2uFKKesFn4do2gD3ruF-g6TfeP5o9hxuqY19fnw7So6vbdxaJ806sec-UZmAdmuRrDrogAHuU1Qmw14z4pLK6Hqm2qdF=s0-d)
![[4dyz]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_vwD77csybtxwWUNIHuKcN2fcXU3g_T2jemVJuxv9sYqu8KEVS04Iy-dfm0gDDlzyrwYQTNe1HV01Ti1CEZxRoxGet2RXqWs2IFSCbP9kmF4z3owcA4kApYiXpdtx3wOoS-DV7grG-Y9avd=s0-d)
![[4dx2-y2]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_v1UTHGbY6CZPA-uveaie9vhHfyWu3BF8rmEVvXhWLgtMTrY6jrUKEW6W9DO5TLqMxlWKsIWxh6hovlwszBPtuxS2skiOHrPSmW8nbye8WdI16PSAUs_3lE050fr7qdWmKskJszBXE7ZfMXEGF5=s0-d)
![[4dz2]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_vjAIjS9U2AHab6bTR_R_C50TSi0pFw9SGVgBFBsVM2mX0t9yjtcTxkl-2P3jc0cBQgRIKDl25P-6PWbHH4fYJq-1yiSR8KUw5CLG9-XKi0dsd5enMA2_lVgIonRhe6gpzYOJIDM9sD9fE=s0-d)
![[4fz3]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_sg2TZ0b4Gu9i93Sv-xCAMNYWy17nTL-lXHZ21kWhJNXrlUupkfh-9d5BZlktHr3iA-l8kvEE4hLBZvSURurnMx6ZF8cRiad_6hmXcZiDNsjgzDJ1dh_Srjn7TZxdZkyt73DipbnSnB-nPf=s0-d)
![[4fxz2]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_tLOZZlc0JjZiFzAWTZlupXQHidPwMW0S6cXvdKecvhXEBafmh-O5lSwuxM-KF3-sTQHTvn560ze5zYVeoLmCFxrWQA-x1q-s36_PLne74nf-Lbv3ivMLOuwlJs-gUR8H1x5CuV4FQ5r6Ws=s0-d)
![[4fyz2]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_s3m65h-WmWYlcaoywDbEBViK-PqE_xYOhPfCg847-jeBZxhD45taDDL7xbGTJUn8qQ_v5_K9wbK05rh3xyVTP8h_BA-WAz7g1Zb-kyO041pnSwC3K91JEZ2oEnYVbr1qLDUIveYnqqh7iu=s0-d)
![[4fxyz]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_tTJbSEkUS9oM-gJt6GNr4IpjSn0w6py30BZiwwOn4J-4GVwYbOw_n4kjAw62XFle4eDGF48r9VBewwb9p6QBA0f7uFsndJEIm1zyBIR8yOihJ9UcEkiwLlL4OpXPAt6sCdvn7dk5RbQmxZCA=s0-d)
![[4fz(x2-y2)]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_sl0l6nnN3iyvQ6DSze1nZ_-gv7N95V-6739kpIUx8I3EvtMntKj4M_K8fU_5MimWY2thvzAEK4plBUJVhztc_B50AD8QdntOD1X8efSEM6B9Cajplo_kkvDpSWJUoyl9ehzG3ZtqFHAH41YsUDuw=s0-d)
![[4fx(x2-3y2)]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_vzdcG6MhnwETNwSkIJk35nm2mMixaUbrWUWOBKOblcJR1AZ60kWC6Exx4BNIIW76ZCRQoQGY_DIy3AMtimky9akQPPpPv3A83s0WEmeId8CfCAr_I_INsfwCUVEqluqnJzbqOfGIRzQbhdoOLn=s0-d)
![[4fy(3x2-y2)]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_uTPJHotkuYN0AdyD-r9A3dDoQA_LPOrKvZSzaZssKRE36VgOML_gPu1rgSi2WghsHJsvYS7VBgKZZqPkqyinGvSQj7b2O_CTrfmGdwUaw7E8jP8quMGsd-su6iA5AnXzKX2zYlUGtvgRKsYqXz=s0-d)
En 1.927 pudo comprobarse experimentalmente la hipótesis de De Broglie al observarse uncomportamiento ondulatorio de los electrones en los fenómenos de difracción.
Un electrón que se mueve alrededor de núcleo puede considerarse ligado a él y podemos describir su movimiento ondulatorio mediante la ecuación de ondas.
Con esta idea, Schrödinger realizó un estudio matemático del comportamiento del electrón en el átomo y obtuvo una expresión, conocida como ecuación de Schrödinger.
Podemos decir que un orbital atómico es una zona del espacio donde existe una alta probabilidad (superior al 90%) de encontrar al electrón. Esto supone considerar al electrón como una nube difusa de carga alrededor del núcleo con mayor densidad en las zonas donde la probabilidad de que se encuentre dicho electrón es mayor.
Para que la ecuación de Schrödinger tenga significado físico es necesario imponerle unas restricciones que son conocidas como números cuánticos, que se simbolizan de la misma forma que los obtenidos en el modelo atómico de Bohr:
Números cuánticos
| |
| n: | número cuántico principal |
| l: | número cuántico del momento angular orbital |
| m: | número cuántico magnético |
| s: | número cuántico del spin electrónico. |
Valores permitidos
| |
| para n: | números enteros 1, 2, 3,. |
| para l: | números enteros desde 0 hasta (n-1) |
| para m: | todos los números enteros entre +l y -l incluido el 0 |
| para s: | sólo los números fraccionarios -1/2 y +1/2 |
Los valores del número cuántico l definen el tipo de orbital:
• Si l= 0 el orbital es del tipo s
• Si l= 1 los orbitales son del tipo p
• Si l = 2 los orbitales son del tipo d
• Si l= 3 los orbitales son del tipo f
Las letras s, p, d, f identificativas de los tipos de orbitales proceden de los nombres que recibieron los distintos grupos de líneas espectrales relacionadas con cada uno de los orbitales:
• sharp : líneas nítidas pero de poca intensidad• principal : líneas intensas
• difuse : líneas difusas
• fundamental : líneas frecuentes en muchos espectros
Son posibles otros tipos de orbitales como g, h, ...pero los elementos que conocemos, en sus estado fundamental, no presentan electrones que cumplan las condiciones cuánticas necesarias para que se den estos otros tipos de orbitales.
Los valores del número cuántico m hacen referencia a la orientación espacial del orbital.
El cuarto número cuántico, s, que define a un electrón en un átomo hace referencia al momento angular de giro del mismo.
Los valores del número cuántico m hacen referencia a la orientación espacial del orbital.
El cuarto número cuántico, s, que define a un electrón en un átomo hace referencia al momento angular de giro del mismo.
El conjunto de los cuatro números cuánticos definen a un electrón, no pudiendo existir en un mismo átomo dos electrones con los cuatro números cuánticos iguales, por lo que una vez definido el tamaño, el tipo y la orientación de un orbital con los tres primeros números cuánticos, es decir los valores de n, l y m, sólo es posible encontrar un máximo de dos electrones en dicha situación que necesariamente tendrán valores diferentes de su número cuántico de spin.
Veamos los orbitales posibles según el valor de los números cuánticos:
Si n = 1 entonces el número cuantico l sólo puede tomar el valor 0 es decir sólo es posible encontrar un orbital en el primer nivel energético en el que puede haber hasta dos electrones (uno con spin +1/2 y otro con spin -1/2). Este orbital, de apariencia esférica, recibe el nombre de 1s:
Si n = 2 , el número l puede tomar los valores 0 y 1, es decir son posibles los tipos de orbitales sy p. En el caso de que sea l = 0, tenemos el orbital llamado 2s en el que caben dos electrones (uno con spin +1/2 y otro con spin -1/2):
Si l = 1 tendremos orbitales del tipo p de los que habrá tres diferentes según indicarían los tres valores (+1, 0, -1) posibles del número cuántico m, pudiendo albergar un máximo de dos electrones cada uno, con valores de spin +1/2 y -1/2, es decir seis electrones como máximo:
Si n = 3 son posibles tres valores del número cuántico l: 0,1 y 2. Si l = 0 tendremos de nuevo un orbital del tipo s:
y si l = 2 los orbitales serán del tipo d, de los que habrá cinco diferentes según indican los cinco valores posibles (+2, +1, 0, -1, -2) para el número cuántico m y que podrán albergar un total de diez electrones:
Si n = 4, son posibles cuatro tipos de orbitales diferentes:
De tipo s (para l = 0):
De tipo f (para l = 3) de los que habrá siete diferentes según indican los siete valores posibles (+3, +2, +1, 0 -1, -2, -3) del número cuántico m, que podrán albergar un total de catorce electrones:




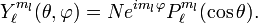








































No hay comentarios:
Publicar un comentario