Algoritmos de búsqueda de raíces
método de la regula falsi (regla del falso) o falsa posición es un método iterativo de resolución numérica de ecuaciones no lineales. El método combina el método de bisección y el método de la secante.
El método
Como en el método de bisección, se parte de un intervalo inicial [a0,b0] con f(a0) y f(b0) de signos opuestos, lo que garantiza que en su interior hay al menos una raíz (véase Teorema de Bolzano). El algoritmo va obteniendo sucesivamente en cada paso un intervalo más pequeño [ak, bk] que sigue incluyendo una raíz de la función f.
A partir de un intervalo [ak, bk] se calcula un punto interior ck:
Dicho punto es la intersección de la recta que pasa por (a,f(ak)) y (b,f(bk)) con el eje de abscisas (igual a como se hace en el método de la secante).
Se evalúa entonces f(ck). Si es suficientemente pequeño, ck es la raíz buscada. Si no, el próximo intervalo [ak+1, bk+1] será:
- [ak, ck] si f(ak) y f(ck) tienen signos opuestos;
- [ck, bk] en caso contrario.
Análisis del método
Se puede demostrar que bajo ciertas condiciones el método de la falsa posición tiene orden de convergencia lineal, por lo que suele converger más lentamente a la solución de la ecuación que el método de la secante, aunque a diferencia de en el método de la secante el método de la falsa posición siempre converge a una solución de la ecuación.
El algoritmo tiene el inconveniente de que si la función es convexa o cóncava cerca de la solución, el extremo del intervalo más alejado de la solución queda fijo variando únicamente el más cercano, convergiendo muy lentamente.
Un ejemplo de este fenómeno se da en la función:
comenzando con [−1,1]. El extremo izquierdo del intervalo, −1, nunca cambia; el extremo derecho se aproxima a 0 linealmente.
La situación en que el método falla es fácil de detectar (el mismo extremo del intervalo se elige dos veces seguidas) y fácil de corregir eligiendo un ck diferente, como:
o
restándole peso a uno de los extremos del intervalo para obligar a que el próximo ck ocurra de ese lado de la función.
El factor 2 usado arriba, garantiza una convergencia superlineal (asintóticamente, el algoritmo ejecuta dos pasos normales por cada paso modificado). Hay otras formas que dan incluso mejores tasas de convergencia. El ajuste mencionado arriba, y otras modificaciones similares se conocen como Algoritmo Illinois. Ford1 resume y analiza las variantes superlineales del método regula falsi modificado. A juzgar por la bibliografía, estos métodos eran bien conocidos en los años 1970 pero han sido olvidados en los textos actuales.
MÉTODO REGLA FALSA
OBJETIVO MÉTODO
Encontrar la intersección de una recta conformada por los puntos a y b con el eje x, y obtener nuevos intervalos mas pequeños, lo la cual permite una aproximación a una raíz.
GENERALIDADES
Este método conserva todas las características y condiciones que posee el método de bisección, excepto por la forma de calcular el punto intermedio del intervalo
Para aplicar el método se debe tener en cuenta:
Xm= a - ((f(a)*(b - a))/(f(b) - f(a)))
El método de Regla Falsa converge más rápidamente que el de bisección porque al permanecer uno de sus valores iniciales fijo el número de cálculos se reduce mientras que el otro valor inicial converge hacia la raíz.
Método para la división de cualquier polinomio entre un binomio de la forma
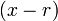 , obteniendo el cociente y elr esto. Descrita por Paolo Ruffini en 1809, es un caso especial de «división sintética» (una división de polinomios en donde el divisor es un «factor lineal»).1 El Algoritmo de Horner para la división de polinomios utiliza la regla de Ruffini. La regla de Ruffini permite asimismo localizar las raíces de un polinomio y factorizarlo en binomios de la forma , obteniendo el cociente y elr esto. Descrita por Paolo Ruffini en 1809, es un caso especial de «división sintética» (una división de polinomios en donde el divisor es un «factor lineal»).1 El Algoritmo de Horner para la división de polinomios utiliza la regla de Ruffini. La regla de Ruffini permite asimismo localizar las raíces de un polinomio y factorizarlo en binomios de la forma 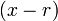 (siendo r un número entero) si es coherente. (siendo r un número entero) si es coherente.Algoritmo
La regla de Ruffini establece un método para la división del polinomio:
entre el binomio:
para obtener el cociente:
y el resto:
Los valores b son los coeficientes del polinomio resultante
 de grado uno menos que el grado de de grado uno menos que el grado de  . El residuo es . El residuo es  Ejemplo 1
División de
entre
utilizando la regla de Ruffini.
1. Se escribe
 y el primer coeficiente (2) en el primer renglón: y el primer coeficiente (2) en el primer renglón:
2. Multiplicando por la raíz r=(-1):
3. Sumando la columna:
4. El procedimiento se repite hasta obtener el residuo:
Si el polinomio original = divisor×cociente+resto, entonces
Ejemplo 2
Cuando el resto es igual a 0; permite factorizar, como en el siguiente ejemplo:
Tomamos
Usamos el método, y nos queda así:
Entonces F(x) se factoriza
 REGLA DE RUFFINILa regla de Ruffini es un algoritmo que permite obtener fácilmente el cociente y el resto de la división de un polinomio por un binomio de la forma x-a. Veamos el algoritmo con un ejemplo, consideremos P(x)=2x3 + x2 - 3x + 5 y Q(x)=x-1. La división se realiza como sigue: 2. Se multiplica el coeficiente que se ha bajado (2) por el que se ha colocado a la izquierda (1). El resultado del producto se coloca debajo del coeficiente del término siguiente y se suman. Figura 2 3. El resultado de la suma se vuelve a multiplicar por el número situado a la izquierda y se repite el proceso. Figuras 3 y 4. 4. El último número (recuadro rojo en Fig. 4) se corresponde con el resto de la división mientras que el resto de números de la fila inferior son los coeficientes del cociente. Resto = 5 y C(x)=2x2 + 3x por tanto 2x3 + x2 - 3x + 5 =(x-1) (2x2 + 3x) +5 |



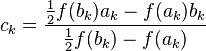
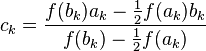









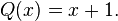




 , donde
, donde y
y 
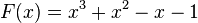
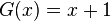

No hay comentarios:
Publicar un comentario