Apuntes de Cinemática

Movimiento rectilíneo

Magnitudes cinemáticas

Se denomina movimiento rectilíneo, aquél cuya trayectoria es una línea recta.

En la recta situamos un origen O, donde estará un observador que medirá la posición del móvil x en el instante t. Las posiciones serán positivas si el móvil está a la derecha del origen y negativas si está a la izquierda del origen.

Posición

La posición x del móvil se puede relacionar con el tiempo t mediante una función x=f(t).

Desplazamiento

Supongamos ahora que en el tiempo t, el móvil se encuentra en posición x, más tarde, en el instante t' el móvil se encontrará en la posición x'. Decimos que móvil se ha desplazado Δx=x'-x en el intervalo de tiempo Δt=t'-t, medido desde el instante t al instante t'.

Velocidad

La velocidad media entre los instantes t y t' está definida por

<v>=x'−xt'−t=ΔxΔt${\displaystyle <v>=\frac{x\text{'}-x}{t\text{'}-t}=\frac{\Delta x}{\Delta t}}$

Para determinar la velocidad en el instante t, debemos hacer el intervalo de tiempo Δt tan pequeño como sea posible, en el límite cuando Δt tiende a cero.

v=limΔ t→0ΔxΔt=dxdt${\displaystyle v=\underset{\Delta t\to 0}{\lim }\frac{\Delta x}{\Delta t}=\frac{dx}{dt}}$

Pero dicho límite, es la definición de derivada de x con respecto del tiempo t.

Para comprender mejor el concepto de velocidad media, resolvemos el siguiente ejercicio

Ejercicio

Una partícula se mueve a lo largo del eje X, de manera que su posición en cualquier instante t está dada porx=5·t²+1, donde x se expresa en metros y t en segundos.

Calcular su velocidad promedio en el intervalo de tiempo entre:

• 2 y 3 s.
• 2 y 2.1 s.
• 2 y 2.01 s.
• 2 y 2.001 s.
• 2 y 2.0001 s.
• Calcula la velocidad en el instante t=2 s.

En el instante t=2 s, x=21 m
t’ (s)	x’ (m)	Δx=x'-x	Δt=t'-t	m/s
3	46	25	1	25>
2.1	23.05	2.05	0.1	20.5
2.01	21.2005	0.2005	0.01	20.05
2.001	21.020005	0.020005	0.001	20.005
2.0001	21.00200005	0.00200005	0.0001	20.0005
...	...	...	...	...
			0	20

Como podemos apreciar en la tabla, cuando el intervalo Δt→0, la velocidad media tiende a 20 m/s. La velocidad en el instante t=2 s es una velocidad media calculada en un intervalo de tiempo que tiende a cero.

Calculamos la velocidad en cualquier instante t

• La posición del móvil en el instante t es x=5t²+1
• La posición del móvil en el instante t+Δt es  x'=5(t+Δt)²+1=5t²+10tΔt+5Δt²+1
• El desplazamiento es Δx=x'-x=10tΔt+5Δt²
• La velocidad media <v> es

<v>=10t⋅Δt+5⋅Δt2Δt=10t+5⋅Δt${\displaystyle <v>=\frac{10t·\Delta t+5·\Delta t^2}{\Delta t}=10t+5·\Delta t}$

La velocidad en el instante t es el límite de la velocidad media cuando el intervalo de tiempo tiende a cero

v=limΔ t→0<v>=limΔ t→0(10t+5Δt)=10t m/s${\displaystyle v=\underset{\Delta t\to 0}{\lim }<v>=\underset{\Delta \mathrm{<mtext\; style="transition:\; none;">\hspace{0.17em}</mtext>t}\to 0}{\lim }\left(10t+5\Delta t\right)=10t\text{m/s}}$

La velocidad en un instante t se puede calcular directamente, hallando la derivada de la posición x respecto del tiempo.

x=5t2+1 mv=dxdt=10t m/s${\displaystyle \begin{array}{l}x=5t^2+1\text{m}\\ v=\frac{dx}{dt}=10t\text{m/s}\end{array}}$

En el instante t=2 s, v=20 m/s

Aceleración

En general, la velocidad de un cuerpo es una función del tiempo. Supongamos que en un instante t la velocidad del móvil es v, y en el instante t' la velocidad del móvil es v'. Se denomina aceleración media entre los instantes ty t' al cociente entre el cambio de velocidad Δv=v'-v y el intervalo de tiempo en el que se ha tardado en efectuar dicho cambio, Δt=t'-t.

<a>=v'−vt'−t=ΔvΔt${\displaystyle <a>=\frac{v\text{'}-v}{t\text{'}-t}=\frac{\Delta v}{\Delta t}}$

La aceleración en el instante t es el límite de la aceleración media cuando el intervalo Δt tiende a cero, que es la definición de la derivada de v.

a=limΔ t→0ΔvΔt=dvdt${\displaystyle a=\underset{\Delta t\to 0}{\lim }\frac{\Delta v}{\Delta t}=\frac{dv}{dt}}$

Ejemplo:

Un cuerpo se mueve a lo largo de una línea recta x=2t³-4t²+5 m. Hallar la expresión de

• La velocidad
• La aceleración del móvil en función del tiempo.

v=dxdt=6t2−8t m/sa=dvdt=12−8 m/s2${\displaystyle \begin{array}{l}v=\frac{dx}{dt}=6t^2-8t\text{m/s}\\ a=\frac{dv}{dt}=12-8{\text{m/s}}^{\text{2}}\end{array}}$

Dada la velocidad del móvil hallar el desplazamiento

Si conocemos un registro de la velocidad podemos calcular el desplazamiento x-x₀ del móvil entre los instantes t₀y t, mediante la integral definida.

x−x0=∫t0tv⋅dt${\displaystyle x-x_0=\underset{t_0}{\overset{t}{\int }}v\cdot dt}$

El producto v dt representa el desplazamiento del móvil entre los instantes t y t+dt, o en el intervalo dt. El desplazamiento total es la suma de los infinitos desplazamientos infinitesimales entre los instantes t₀ y t.

En la figura, se muestra una gráfica de la velocidad en función del tiempo, el área en color azul mide el desplazamiento total del móvil entre los instantes t₀ y t, el segmento en color azul marcado en la trayectoria recta.

Hallamos la posición x del móvil en el instante t, sumando la posición inicial x₀ al desplazamiento, calculado mediante la medida del área bajo la curva v-to mediante cálculo de la integral definida en la fórmula anterior.

Ejemplo:

Un cuerpo se mueve a lo largo de una línea recta de acuerdo a la ley v=t³-4t² +5 m/s. Si en el instante t₀=2 s. está situado en x₀=4 m del origen. Calcular la posición x del móvil en cualquier instante.

x−4=∫2t(t3−4t2+5)dtx=14t4−43t3+5t+23 m${\displaystyle \begin{array}{l}x-4=\underset{2}{\overset{t}{\int }}(t^3-4t^2+5)dt\\ x=\frac{1}{4}{t}^4-\frac{4}{3}{t}^3+5t+\frac{2}{3}\text{m}\end{array}}$

Dada la aceleración del móvil hallar el cambio de velocidad

Del mismo modo, que hemos calculado el desplazamiento del móvil entre los instantes t₀ y t, a partir de un registro de la velocidad v en función del tiempo t, podemos calcular el cambio de velocidad v-v₀ que experimenta el móvil entre dichos instantes, a partir de un registro de la aceleración en función del tiempo.

[Math Processing Error]

En la figura,  el cambio de velocidad v-v₀ es el área bajo la curva a-t, o el valor numérico de la integral definida en la fórmula anterior.

Conociendo el cambio de velocidad v-v₀, y el valor inicial v₀ en el instante t₀, podemos calcular la velocidad v en el instante t.

Ejemplo:

La aceleración de un cuerpo que se mueve a lo largo de una línea recta viene dada por la expresión. a=4-t² m/s². Sabiendo que en el instante t₀=3 s, la velocidad del móvil vale v₀=2 m/s. Determinar la expresión de la velocidad del móvil en cualquier instante

v−2=∫3t(4−t2)dtv=4t−13t3−1 m/s${\displaystyle \begin{array}{l}v-2=\underset{3}{\overset{t}{\int }}(4-t^2)dt\\ v=4t-\frac{1}{3}{t}^3-1\text{m/s}\end{array}}$

Resumiendo, las fórmulas empleadas para resolver problemas de movimiento rectilíneo son

v=dxdt  x−x0=∫t0tv⋅dta=dvdt  v−v0=∫t0ta⋅dt

movimiento rectilíneo uniforme o m.r.u en la naturaleza es bastante extraño, es el movimiento más fácil de estudiar y nos servirá para estudiar otros más complejos. El movimiento rectilíneo uniforme cumple las siguientes propiedades:

• La aceleración es cero (a=0) al no cambiar la velocidad de dirección ni variar su módulo
• Por otro lado, la velocidad inicial, media e instantánea del movimiento tienen el mismo valor en todo momento

Un cuerpo realiza un movimiento rectilíneo uniforme cuando su trayectoria es una linea recta y suvelocidad es constante. Esto implica que recorre distancias iguales en tiempos iguales.

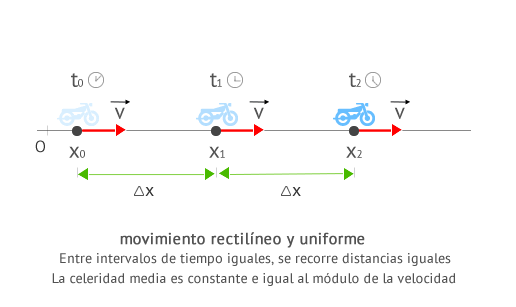
Ecuaciones de m.r.u.

Las ecuaciones del movimiento rectilíneo uniforme son:

x=x0+v⋅t

v=v0=cte

a=0

Donde:

• x, x0: La posición del cuerpo en un instante dado (x) y en el instante inicial (x0). Su unidad en el Sistema Internacional (S.I.) es el metro (m)
• v,v0: La velocidad del cuerpo en un instante dado (v) y en el instante inicial (v0). Su unidad en el Sistema Internacional (S.I.) es el metro por segundo (m/s)
• a: La aceleración del cuerpo. Su unidad de medida en el Sistema Internacional (S.I.) es el metro por segundo al cuadrado (m/s2)

Para deducir las ecuaciones del movimiento rectilíneo uniforme m.r.u. hay que tener en cuenta que:

• La velocidad media coincide con la velocidad instantánea
• No hay aceleración

Con esas restricciones nos queda:

vm=vvm=ΔxΔt=x−x0t−t0=t0=0x−x0t⎫⎭⎬⎪⎪→x−x0=v⋅t→x=x0+v⋅t

Ejemplo

Dos jugadores de canicas se encuentran uno frente a otro con sus canicas en la mano. El juego consiste en lanzarlas al mismo tiempo en línea recta y hacer que ambas se golpeen. Si ambos se encuentran situados a 36 metros uno del otro y el jugador A lanza su canica a 2 m/sg y el jugador B a 4 m/sg en un movimiento rectilíneo uniforme. Calcula a que distancia del jugador B chocarán las canicas.

Solución

Datos

Considerando que la canica del jugador A se encuentra en el origen de coordenadas:

Canica A
X0=0 m
VA=2 m/sg

Canica B
X0=36 m
VB=-4 m/sg (se desplaza hacia el origen del sistema de referencia)

Resolución

Considerando inicialmente el sistema de referencia comentado en los datos, vamos a estudiar la ecuación de la posición de cada una de las canicas por separado.

En un m.r.u. la posición de un cuerpo en movimiento viene dada por la siguiente ecuación:

x=x0+v⋅t

Canica jugador A.

Sustituyendo los valores de este jugador en la ecuación del m.r.u. obtenemos que:

xA=0+2⋅t m ⇒xA=2⋅t m

Canica jugador B

Sustituyendo nuevamente en la ecuación, pero con los datos del jugador B:

xB=36−4⋅t m

Observa que al desplazarse hacia el origen de nuestro sistema de referencia su velocidad es negativa.

Ambas canicas impactarán cuando sus posiciones sean las mismas, es decir XA=XB, por tanto:

XA=XB⇒2⋅t=36−4⋅t⇒t=366⇒t=6 sg

Es decir, cuando transcurran 6 sg chocarán, pero ¿donde?. Como sabemos cuando se produce el impacto, basta sustituir ese tiempo en la ecuación de la posición de cualquiera de las 2 canicas.

XA=2⋅t⇒XA=2⋅6⇒XA=12 m

Por tanto, el choque se produce a 12 metros del jugador A y a 24 m (36-12) del jugador B.

Movimiento rectilíneo uniforme

Un movimiento rectilíneo uniforme es aquél cuya velocidad es constante, por tanto, la aceleración es cero. La posición x del móvil en el instante t lo podemos calcular integrando

x−x0=v⋅(t−t0)${\displaystyle x-x_0=v\cdot \left(t-t_0\right)}$

o gráficamente, en la representación de v en función de t.

Habitualmente, el instante inicial t₀ se toma como cero, por lo que las ecuaciones del movimiento uniforme resultan

a=0v=ctex=x0+v⋅t${\displaystyle \begin{array}{l}a=0\\ v=\text{cte}\\ x=x_0+v\cdot t\end{array}}$

Movimiento rectilíneo uniformemente acelerado

Un movimiento uniformemente acelerado es aquél cuya aceleración es constante. Dada la aceleración podemos obtener el cambio de velocidad v-v₀ entre los instantes t₀ y t, mediante integración, o gráficamente.

v−v0=a⋅(t−t0)${\displaystyle v-v_0=a\cdot \left(t-t_0\right)}$

Dada la velocidad en función del tiempo, obtenemos el desplazamiento x-x₀ del móvil entre los instantes t₀ y t, gráficamente (área de un rectángulo + área de un triángulo), o integrando

x−x0=v0⋅(t−t0)+12⋅a⋅(t−t0)2${\displaystyle x-x_0=v_0\cdot \left(t-t_0\right)+\frac{1}{2}\cdot a\cdot {\left(t-t_0\right)}^2}$

Habitualmente, el instante inicial t₀ se toma como cero, quedando las fórmulas del movimiento rectilíneo uniformemente acelerado, las siguientes.

a=ctev=v0+a⋅tx=x0+v0⋅t+12⋅a⋅t2${\displaystyle \begin{array}{l}a=\text{cte}\\ v=v_0+a\cdot t\\ x=x_{\text{0}}+v_0\cdot t+\frac{1}{2}\cdot a\cdot t^2\end{array}}$

Despejando el tiempo t en la segunda ecuación  y sustituyéndola en la tercera, relacionamos la velocidad v con el desplazamiento x-x₀

v2=v20+2a(x−x0)

derivada del movimiento rectilíneo

Interpretación geométrica de la derivada

El siguiente applet, nos puede ayudar a entender el concepto de derivada y la interpretación geométrica de la derivada

v=limΔ t→0ΔxΔt=dxdt${\displaystyle v=\underset{\Delta t\to 0}{\lim }\frac{\Delta x}{\Delta t}=\frac{dx}{dt}}$

Se elige la función a representar en el control de selección titulado Función,  entre las siguientes:

x=16t3−73t2+172tx=13t+5x=8⋅sin(π10t)${\displaystyle \begin{array}{l}x=\frac{1}{6}{t}^3-\frac{7}{3}{t}^2+\frac{17}{2}t\\ x=\frac{1}{3}t+5\\ x=8·\text{sin}\left(\frac{\pi }{10}t\right)\end{array}}$

Se pulsa el botón titulado Nuevo

Se observa la representación de la función elegida

Con el puntero del ratón se mueve el cuadrado de color azul, para seleccionar una abscisa t₀.

Se elige el aumento, 10, 100, ó 1000 en el control de selección titulado Aumento

• Cuando se elige 100 ó 1000, la representación gráfica de la función es casi un segmento rectilíneo. Se mide su pendiente con ayuda de la rejilla trazada sobre la representación gráfica
• Se calcula la derivada de la función en el punto de abscisa t₀ elegido
• Se comprueba si coinciden la medida de la pendiente y el valor de la derivada en t₀.

Ejemplo:

Elegimos la primera función y el punto t₀=3.009

Elegimos ampliación 1000.  La pendiente de la recta vale -1, y se muestra en la figura.

La derivada de dicha función es

dxdt=12t2−143t+172${\displaystyle \frac{dx}{dt}=\frac{1}{2}{t}^2-\frac{14}{3}t+\frac{17}{2}}$

para t₀=3.0 la derivada tiene vale -1.0

Integral definida

Dada la velocidad del móvil en función del tiempo, vamos a calcular el desplazamiento del móvil entre los instantes t₀ y t.  En los casos en los que la velocidad es constante o varía linealmente con el tiempo, el desplazamiento se calcula fácilmente

Si v=35 m/s, el desplazamiento del móvil entre los instantest₀=0 y t=10 s es Δx=35·10=350 m

Si v=6·t, el desplazamiento del móvil entre los instantest₀=0 y t=10 s es el área del triángulo de color azul claro Δx=(60·10)/2=300 m

Si v=-8·t+60. el desplazamiento del móvil entre los instantest₀=0 y t=10 s es la suma de las áreas de dos triángulos:

• el de la izquierda tiene un área de (7.5·60)/2=225 
• el de la derecha tiene un área de (-20·2.5)/2=-25.

El desplazamiento es el área total Δx=225+(-25)=200 m

En otros casos, podemos calcular el desplazamiento aproximado, siguiendo el procedimiento que se muestra en la figura

En el instante t_i-1 la velocidad del móvil es v_i-1, en el instante t_i la velocidad del móvil es v_i. La velocidad media <v_i> en el intervalo de tiempo Δt_i=t_i-t_i-1 comprendido entre t_i-1 y t_i es

<vi>=v(ti)+v(ti−1)2${\displaystyle <v_i>=\frac{v(t_i)+v(t_{i-1})}{2}}$

El desplazamiento del móvil durante el intervalo de tiempo Δt_i=t_i-t_i-1 comprendido entre t_i-1 y t_i es aproximadamente el área del rectángulo <v_i>·Δt_i. El desplazamiento total x-x₀ entre el instante inicial t₀, y el instante final t=t_n es, aproximadamente

x−x0≈∑i=1n<vi>Δti${\displaystyle x-x_0\approx \sum _{i=1}^n<v_i>\Delta t_i}$

donde n es el número de intervalos

Si v=-t²+14t+21 (m/s) y tomamos n=10 intervalos iguales, entre el instante t₀=0 y t=10 s el desplazamiento aproximado vale

x-x₀≈27.7+39.8+49.8+57.7+63.7+67.7+69.7+69.8+67.8+63.8=577.5 m

Cuando el número de intervalos en los que se ha dividido un intervalo dado (t₀, t) es muy grande Δt_i→0. En el límite, el desplazamiento se expresa como

x−x0=∫t0tv⋅dt${\displaystyle x-x_0=\underset{t_0}{\overset{t}{\int }}v·dt}$

Si v=-t²+14t+21 (m/s), el desplazamiento entre el instante t₀=0 y t=10 s vale

x−x0=∫010(−t2+14t+21)⋅dt=−t33+7t2+21t∣∣∣100=17303 m