Historia de los matemáticos más famosos

Al-Juarismi

Abu Abdallah Muḥammad ibn Mūsā al-Jwārizmī (Abu Yāffar) (أبو عبد الله محمد بن موسى الخوارزمي ابو جعفر), conocido generalmente como al-Juarismi, fue un matemático, astrónomo y geógrafo; persa^1 2 musulmán, que vivió aproximadamente entre 780 y 850.

Poco se conoce de su biografía, a tal punto que existen discusiones no saldadas sobre su lugar de nacimiento. Algunos sostienen que nació en Bagdad. Otros, siguiendo el artículo de Gerald Toomer³ (a su vez, basado en escritos del historiador al-Tabari) sostienen que nació en la ciudad corasmia de Jiva, en el actual Uzbekistán. Rashed⁴ halla que se trata de un error de interpretación de Toomer, debido a un error de transcripción (la falta de la conectiva wa) en una copia del manuscrito de al-Tabari. No será este el último desacuerdo entre historiadores que encontraremos en las descripciones de la vida y las obras de al-Juarismi. Estudió y trabajó en Bagdad en la primera mitad del siglo IX, en la corte del califa al-Mamun. Para muchos, fue el más grande de los matemáticos de su época.

Debemos a su nombre y al de su obra principal, "Hisāb al-ŷabr wa'l muqābala", (حساب الجبر و المقابلة) nuestras palabras álgebra,guarismo y algoritmo. De hecho, es considerado como el padre del álgebra y como el introductor de nuestro sistema de numeración denominado arábigo.

Hacia 815 al-Mamun, séptimo califa Abásida, hijo de Harún al-Rashid, fundó en su capital, Bagdad, la Casa de la sabiduría(Bayt al-Hikma), una institución de investigación y traducción que algunos han comparado con la Biblioteca de Alejandría. En ella se tradujeron al árabe obras científicas y filosóficas griegas e hindúes. Contaba también con observatorios astronómicos. En este ambiente científico y multicultural se educó y trabajó al-Juarismi junto con otros científicos como los hermanos Banu Musa,al-Kindi y el famoso traductor Hunayn ibn Ishaq. Dos de sus obras, sus tratados de álgebra y astronomía, están dedicadas al propio califa.

Álgebra

Primera página de Kitāb al-mukhtaṣar fī ḥisāb al-jabr wa-l-muqābala.

En su tratado de álgebra Hisāb al-ŷabr wa'l muqābala (حساب الجبر و المقابلة, Compendio de cálculo por compleción y comparación), obra eminentemente didáctica, se pretende enseñar un álgebra aplicada a la resolución de problemas de la vida cotidiana del imperio islámico de entonces. La traducción de Rosen de las palabras de al-Juarizmi describiendo los fines de su libro dan cuenta de que el sabio pretendía enseñar:

... aquello que es fácil y más útil en aritmética, tal que los hombres lo requieren constantemente en casos de herencia, legados, particiones, juicios, y comercio, y en todos sus tratos con los demás, o cuando se trata de la mensura de tierras, la excavación decanales, cálculos geométricos, y otros objetos de varias clases y tipos.

Traducido al latín por Gerardo de Cremona, se utilizó en las universidades europeas como libro de texto hasta el siglo XVI. Es posible que antes de él se hubiesen resuelto ecuaciones concretas, pero éste es el primer tratado conocido en el que se hace un estudio exhaustivo.

Luego de presentar los números naturales, al-Juarismi aborda la cuestión principal en la primera parte del libro: la solución de ecuaciones. Sus ecuaciones son lineales o cuadráticas y están compuestas de unidades, raíces y cuadrados; para él, por ejemplo, una unidad era un número, una raíz era  y un cuadrado . Aunque en los ejemplos que siguen usaremos la notación algebraica corriente en nuestros días para ayudar al lector a entender las nociones, es de destacar que al-Juarizmi no empleaba símbolos de ninguna clase, sino sólo palabras.

Primero reduce una ecuación a alguna de seis formas normales:

1. Cuadrados iguales a radicales.
2. Cuadrados iguales a números.
3. Raíces iguales a números.
4. Cuadrados y raíces iguales a números, por ejemplo 
5. Cuadrados y números iguales a raíces, por ejemplo 
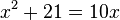
6. Raíces y números iguales a cuadrados, por ejemplo 

La reducción se lleva a cabo utilizando las operaciones de al-ŷabr ("compleción", el proceso de eliminar términos negativos de la ecuación) y al-muqabala ("balanceo", el proceso de reducir los términos positivos de la misma potencia cuando suceden de ambos lados de la ecuación). Luego, al-Juarismi muestra como resolver los seis tipos de ecuaciones, usando métodos de solución algebraicos y geométricos. Por ejemplo, para resolver la ecuación , escribe:

... un cuadrado y diez raíces son iguales a 39 unidades. Entonces, la pregunta en este tipo de ecuación es aproximadamente así: cuál es el cuadrado que, combinado con diez de sus raíces, dará una suma total de 39. La manera de resolver este tipo de ecuación es tomar la mitad de las raíces mencionadas. Ahora, las raíces en el problema que tenemos ante nosotros son diez. Por lo tanto, tomamos 5 que multiplicadas por sí mismas dan 25, una cantidad que agregarás a 39 dando 64. Habiendo extraído la raíz cuadrada de esto, que es 8, sustraemos de allí la mitad de las raíces, 5, resultando 3. Por lo tanto el número tres representa una raíz de este cuadrado.

Álgebra⁵

Sigue la prueba geométrica por compleción del cuadrado, que no expondremos aquí. Señalaremos sin embargo que las pruebas geométricas que usa al-Juarismi son objeto de controversia entre los expertos. La cuestión, que permanece sin respuesta, es si estaba familiarizado con el trabajo de Euclides. Debe recordarse, en la juventud de al-Juarismi y durante el reinado de Harun al-Rashid, al-Hajjaj había traducido los "Elementos" al árabe, y era uno de los compañeros de al-Juarismi en la Casa de la Sabiduría. Esto avalaría la posición de Toomer (op.cit.). Rashed comenta⁶ que "el tratamiento [de al-Juarismi] fue probablemente inspirado en el reciente conocimiento de "los Elementos". Pero, por su parte, Gandz⁷ sostiene que los Elementos le eran completamente desconocidos. Aunque es inseguro que haya efectivamente conocido la obra euclidiana, es posible afirmar que fue influido por otras obras de geometría; véase el tratamiento de Parshall⁸ sobre las similitudes metodológicas con el texto hebreo Mishnat ha Middot, de mediados del siglo II.

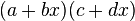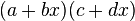Continúa el Hisab al-ŷabr wa'l-muqabala examinando cómo las leyes de la aritmética se extienden a sus objetos algebraicos. Por ejemplo, muestra cómo multiplicar expresiones como . Rashed (op. cit.) encuentra sus formas de resolución extremadamente originales, pero Crossley⁹ las considera menos significativas. Gandz considera que la paternidad del álgebra es mucho más atribuible a al-Juarismi que a Diofanto.¹⁰

La parte siguiente consiste en aplicaciones y ejemplos. Describe reglas para hallar el área de figuras geométricas como el círculo, y el volumen de sólidos como la esfera, el cono y la pirámide. Esta sección, ciertamente, tiene mucha mayor afinidad con los textos hebreos e indios que con cualquier obra griega. La parte final del libro se ocupa de las complejas reglas islámicas de herencia, pero requiere poco del álgebra que expuso anteriormente, más allá de la resolución de ecuaciones lineales.

Aritmética

De su aritmética, posiblemente denominada originalmente Kitab al-Ŷamaa wa al-Tafriq bi Hisab al-Hind, (كتاب الجامع و التفريق بحساب الهند), "libro de la suma y de la resta, según el cálculo indio", sólo conservamos una versión latina del siglo XII, Algoritmi de numero Indorum. Desafortunadamente, se sabe que la obra¹¹ se aparta bastante del texto original. En esta obra se describen con detalle los números indoarábigos, el sistema indio de numeración posicional en base 10 y métodos para hacer cálculos con él. Se sabe que había un método para encontrar raíces cuadradas en la versión árabe, pero no aparece en la versión latina. Posiblemente fue el primero en utilizar elcero como indicador posicional. Fue esencial para la introducción de este sistema de numeración en el mundo árabe, al-Ándalus y posteriormente en Europa. André Allard¹² discute algunos tratados en latín del siglo XII basados en esta obra perdida.

Astronomía

De su tratado sobre astronomía, Sindhind zij, también se han perdido las dos versiones que escribió en árabe. Esta obra¹³ se basa en trabajos astronómicos indios "a diferencia de manuales islámicos de astronomía posteriores, que utilizaron los modelos planetarios griegos del 'Almagesto' de Ptolomeo".¹⁴ El texto indio en que se basa el tratado es uno de los obsequiados a la corte de Bagdad alrededor de 770 por una misión diplomática de la India. En el siglo X al-Maŷriti realizó una revisión crítica de la versión más corta, que fue traducida al latín por Adelardo de Bath; existe también una traducción latina de la versión más larga, y ambas traducciones han llegado hasta nuestro tiempo. Los temas principales cubiertos en la obra son los calendarios; el cálculo de las posiciones verdaderas del Sol, la Luna y los planetas; tablas de senos y tangentes; astronomía esférica; tablas astrológicas; cálculos de paralajes y eclipses; y visibilidad de la Luna. Rozenfel'd analiza un manuscrito relacionado sobre trigonometría esférica,¹⁵ atribuido a al-Juarismi.

Geografía

En Geografía, con una obra denominada Kitab Surat-al-Ard, revisó y corrigió a Ptolomeo en lo referente a África y al Oriente. Lista latitudes y longitudes de 2402 sitios, y emplaza ciudades, montañas, mares, islas, regiones geográficas y ríos, como base para un mapa del mundo entonces conocido. Incluye mapas^{[cita requerida]} que, en conjunto, son más precisos que los de Ptolomeo. Está claro que donde hubo mayor conocimiento local disponible para al-Juarismi, como las regiones del islam, África y el Lejano Oriente, el trabajo es mucho más exacto que el de Ptolomeo, pero parece haber usado los datos de éste para Europa. Se dice que en estos mapas trabajaron a sus órdenes setenta geógrafos.

Otras obras

Su obra conocida se completa con una serie de obras menores sobre temas como el astrolabio, sobre el que escribió dos textos, sobre relojes solares y sobre elcalendario judío. También escribió una historia política conteniendo horóscopos de personajes prominentes.

autores son Fernando Álvarez, Óscar Martín y Cristóbal Pareja.

Bagdad, siglo VIII

Una nueva civilización se acaba de abrir paso en la historia. Arrancó de Arabia hace dos siglos a partir de innumerables tribus nómadas que fueron aglutinadas por la fe de un profeta y el magnetismo de un libro revelado. Hoy, aquel incipiente estado se ha expandido hacia el este mirando a Oriente. Y también ha conquistado Jerusalén y Damasco. Todo el norte de África incova ya al profeta, y también gran parte de la península Ibérica. El mundo musulmán se extiende ya dede la India hasta los Pirineos.

La dinastía Omeya, la fundadora, ha sido destronada por la Abasí. Tres nombres aparecen, tres califas: Al-Mansur, que ha fundado Bagdad y la ha hecho capital, en lugar de la antigua Damasco. Aquí erige la Casa de la Sabiduría, donde las ciencias comienzan a florecer. Al segundo califa, Harún al-Rashid, nos lo ha presentado Scheherezade en numerosas veladas de Las mil y una noches: «He llegado a saber que en tiempo del califa Harún al-Rashid vivía en la ciudad de Bagdad un hombre llamado Simbad...», comienza uno de sus relatos. Su reinado fue el periodo de mayor esplendor cultural, al decir de los historiadores. Por eso se evoca su nombre en cuentos y leyendas. Con el ardor de los pueblos que despiertan, se han traducido al árabe manuscritos griegos, sirios y persas. Pero es en el califatod de Al-Mamún, su hijo, cuando la fiebre traductora alcanza su cima. Llegan textos de la India, en sánscrito, que son de la civilización griega, fruto de las relaciones comerciales con el imperio bizantino. Bagdad hizo con la cultura clásica lo que haría la Escuela de Traductores de Toledo más adelante.

Gracias a estos tres califas benefactores —que el Clemente, el Misericordioso, conserve sus nombres— Bagdad tuvo tiempo suficiente para que sus mejores hijos —originarios de todos los confines del imperio— la convirtiesen en una nueva Alejandría. En esa misma época, Occidente, a pesar de estar unido por el latín, no supo preservar el legado científico clásico. La Iglesia fue la única institución que no se desintegró y que mantuvo cierto impulso intelectual en los monasterios. Pero el monje, incluso el más instruido, tendía en su erudición más al negocio de la salvación del alma que a la filosofía natural. Solamente hubo una tentativa de revivificación cultural con Carlomagno, con la reinstauración de un programa de estudio: el Trivium (gramática, retórica y dialéctica) y el Quadrivium (aritmética, geometría, astronomía y música), heredados de la antigüedad clásica. A pesar de ello, el interés por el saber había desaparecido en el mundo occidental.

Debemos, pues, volver a Bagdad, ya en el siglo IX. Es una ciudad culta y mágica. Aquí, ya se sabe, la gente cruza el Tigris volando sobre alfombras. Y se buscan piedras filosofales y elixires de eterna juventud, a la vez que se traduce a Euclides, se estudia el Almagesto de Ptolomeo y se copian las obras de Arquímedes. En esta ciudad desarrolló su labor creativa Al-Juarismi.

Al-Juarismi escribió un libro que habría de tener gran influencia posterior en Europa. El original árabe se ha perdido y lo conocemos por una copia latina del siglo XII: Algoritmi de Numero Indorum (El arte indio del cálculo de Al-Juarismi). Como se ve en el título, se ha latinizado el nombre del autor. De él derivará la palabra moderna algoritmo.

En el libro se describe pormenorizadamente el sistema indio de numeración, con los 10 dígitos —incluido el cero—, y basado, como hoy, en que el valor de cada cifra depende de su posición: en 444$444$ cada 4$4$ es diferente (4$4$ centenas, 4$4$decenas y 4$4$ unidades). Se describen asimismo las reglas para realizar las cuatro operaciones aritméticas básicas. Y esto es lo más importante, porque ha de recordarse que con el sistema romano se podían escribir números, sí, pero no había manera de calcular: la tarea de sumar era difícil, la de multiplicar solo era posible para los sabios y la de dividir... estaba reservada casi únicamente a los dioses. Hoy día, un niño necesita únicamente pronunciar las palabras mágicas de su tabla de multiplicar y un algoritmo, automático y obediente, proporciona el resultado.

No obstante, los nuevos métodos tardaron en implantarse y el antiguo sistema romano siguió usándose en Europa durante gran parte de la Edad Media. En la figura de la derecha se muestra, en el centro, a la musa de la aritmética; Boecio, a la izquierda, simbolizando la escritura decimal, sonríe por haber acabado una operación; a la derecha, el griego Pitágoras intenta hacer lo mismo con un ábaco, con poco éxito, según el pintor. La pintura, de 1508, evidencia que la supremacía de la escritura decimal posicional, frente a la romana, no era aún reconocida por todos en esa época.

'Al-Jabr' o el Álgebra

La obra más importante de Al-Juarismi lleva el impresionante título de Al-kitab al-muthasar fi hisab al-jabr wa'l-muqabala, que más o menos dice:Libro sobre el método de cálculo consistente en restaurar y equilibrar.

El titulo parece la expresión de un conjuro que hay que pronunciar, mientras se frota una vieja lámpara, para liberar un genio prisionero. Y en verdad así es, pues en el interior del libro, el genio nos revela las fórmulas —¿de alquimia?— para resolver las ecuaciones de primero y segundo grado. Lo hace a través de una colección de problemas de aritmética —sobre herencias, transacciones comerciales, etc.— que resuelve mediante ecuaciones.

La obra nos ha llegado en dos versiones, una árabe una traducción latina, llamda Liber algebrae et almucabala. Sorprende que la versión latina sea más completa. También hay que hacer notar que en esta se omite el prólogo, que sí aparece en la versión árabe. El lector puede imaginar el porqué: es una prudente forma de evitar las preceptivas loas a Mahoma y al Comendador de los Creyentes, a la sazón Al-Mamún. La palabra "álgebra" tiene su origen enal-jabr, presente en el título, que, en árabe, era un término médico: "restaurar y curar huesos fracturados". Esta palabrá pasó a Europa en su traducción latina a través de España y hoy es similar en todos los idiomas europeos.

Todavía pdemos encontrar un vestigio de este antiguo significado en nuestra lengua. En el diccionario de la Real Academia aparece esta acepción: "Arte de restituir los huesos dislocados. Y "algebrista" —en versión árabe— es lo mismo que "traumatólogo" —en versión griega—.

En el capítulo XV del Quijote se alude a la victoria del ingenioso hidalgo sobre el Caballero de los Espejos (que era en realidad el bachiller Sansón Carrasco):

[...] ufano y vanaglorioso iba Don Quijote por haber alcanzado vitoria de tan valiente caballero [...]

Del vencido caballero y de su escudero sigue narrando Cervantes que

[...] llegaron a un pueblo donde fue ventura hallar un algebrista, con quien se curó el Sansón desgraciado [...]

Las ecuaciones

Al-Jabr proporciona un estudio exhaustivo de las ecuaciones de segundo y primer grado. Las clasifica en sesis tipos, que resuelve, con algoritmos —nunca mejor dicho— precisos. Pero, como dice él mismo, es necesario acudir a la geometría para demostrar el método. ¿Estará inspirándolo Arquímedes?

He aquí su clasificación después de haber transformado las ecuaciones hasta tener solo sumas (ninguna resta):

ax2=bx$a{x}^2=bx$	ax2=c$a{x}^2=c$	bx=c$bx=c$
ax2+bx=c$a{x}^2+bx=c$	ax2+c=bx$a{x}^2+c=bx$	bx+c=ax2$bx+c=a{x}^2$

Las dos soluciones de cada ecuación se hallan completando cuadrados. Pero solo considera las positivas.

Hay que decir que la lectura es difícil, porque todavía no existe una notación sincopada (abreviada, simbólica) para los cálculos. Estos se describen con palabras. Incluso para los números usa su nombre en vez de su signo.

El lector puede combrobar por sí mismo cómo narra la resolución de la ecuación de segundo grado x2+10x=39$x^2+10x=39$.

Y he aquí la justificación geométrica que aporta él mismo: la incógnita x$x$, la xai, está representada por el lado del cuadrado en blanco (obsérvese la figura de más abajo). Con ello transforma x2$x^2$ en un área. Para conseguir otra área igual a 10x$10x$, descompone 10$10$ en 4×2,5$4\times 2,5$ y añade los cuatro rectángulos de lados x$x$ y 2,5$2,5$. Ya tenemos representado el primer miembro. A continuación añade los cuatro cuadrados de las esquinas y obtiene el cuadrado grande. Es decir:

x2+10x+4×2,52=39+4×2,52⇒(x+5)2=64⇒x+5=8$$x^2+10x+4\times 2,5^2=39+4\times 2,5^2\Rightarrow (x+5{)}^2=64\Rightarrow x+5=8$$

Un último ejemplo

Otra ecuación que se resuelve en el libro es x2+21=10x$x^2+21=10x$. Hoy, sin miedo a los negativos, la escribiríamos así x2−10x+21=0$x^2-10x+21=0$.

Nuestros estudiantes aprenden que cuando el coeficiente de la x$x$ es par, es decir, cuando tenemos ax2+2b′x+c=0$a{x}^2+2b^{\prime }x+c=0$, conviene expresar la fórmula que proporciona las raíces así: −b′±b′2−ac√a$\frac{-b^{\prime }\pm \sqrt{b^{\prime 2}-ac}}{a}$, pues con ella los cálculos se simplifican notablemente. En nuestro ejemplo queda: x=5±52−21−−−−−−√$x=5\pm \sqrt{5^2-21}$. Pues bien, esta fórmula era conocida por Al-Juarismi. Dejemos que él hable:

La regla exige que tú reduzcas a la mitad el número [el coeficiente] de la x$x$, lo cual da 5$5$. Multiplica este número por sí mismo y tienes 25$25$. Resta 21$21$ del cuadrado, y quedará 4$4$. Extrae la raíz, de donde obtendrás 2$2$, y sustrae este 2$2$ de la mitad del número de la x$x$, o sea, de 5$5$. Así te queda 3$3$. Esta es la raíz que buscas...

De forma análoga, continúa dando la pauta para obtener la segunda raíz, que resulta ser 7$7$. Y advierte inmediatamente de que si la resta que aparece en el radicando fuese cero, habría una sola raíz; y si esa resta no pudiera efectuarse, no habría solución: ¡discusión completa del discriminante!

Como los griegos, Al-Juarismi incluye difíciles demostraciones geométricas para sus reglas. Ello suscita nuestra admiración, pero la geometría no deja de lastrar aquí el advenimiento definitivo del lenguaje algebraico, ese que, pasado el tiempo, cobrará vida propia, pensará por nosotros y tomará las riendas del discurso. Habría que pasar mucho tiempo, empero, hasta que en Occidente las semillas de la India, Persia y Grecia, traídas por el viento del desierto árabe, germinasen definitivamente en el Renacimiento.

... y la justificación geométrica

El lector meticuloso habrá echado de menos el razonamiento dado por Al-Juarismi para la resolución de x2+21=10x$x^2+21=10x$. Helo aquí:

1. Se traza un cuadrado de lado x$x$ y área x2$x^2$ (arriba, a la izquierda).

2. Con un lado común al cuadrado, se traza un rectángulo de área 21$21$ (arriba, a la derecha). El área del rectángulo conjunto resultante ha de ser, según la ecuación, igual a 10x$10x$, luego su base es 10$10$.

3. Trazamos la mediatriz del segmento base de este gran rectángulo y formamos el nuevo cuadrado, grande, de lado 5$5$. Formamos también un cuadrado interior al anterior de lado 5−x$5-x$. Los dos rectángulos marcados con la letra A$A$ tienen las mismas dimensiones y, en consecuencia, la misma área.

4. El área del cuadrado de lado 5$5$ puede ahora expresarse de dos formas:

52=21+(5−x)2⇒4=(5−x)2⇒2=5−x⇒x=3