Aryabhata
Aryabhata o Aryabhata I4 5 (hacia 476-550) fue el primer gran matemático y astrónomo de la era clásica de lamatemática en la India y la astronomía india.
La obra de Aryabhata trata principalmente sobre la matemática y la astronomía; también trabajó en la aproximación del número π.
Biografía
Nombre
- Āryabhaṭa en el sistema AITS (alfabeto internacional de transliteración sánscrita)
- [ariabáta] (pronunciación aproximada)
- आर्यभटः en letra devanagari para la escritura del idioma sánscrito
A pesar de que es usual transliterar su nombre como Aryabhatta ―en analogía con otros nombres que tienen el sufijo "bhatta"―, el nombre correcto es Aryabhaṭa o Aryabhata: cada texto astronómico deletrea su nombre así,6 incluyendo las más de cien veces en que Brahmagupta lo nombra.7
Fecha y lugar de nacimiento
Aryabhata menciona en el Aryabhatiya que había comprendido 3630 años en la era de Kali iuga, cuando tenía 23 años. Esto corresponde al año 499, e implica que había nacido en 476.3
Aryabhata nació en Taregana (literalmente, 'canción de las estrellas'), el cual es un pequeño pueblo en Bihar, India, alrededor de 30 km de la ciudad Pataliputra(actualmente Patna), y que actualmente la capital del estado de Bihar. Las evidencias justifican su nacimiento ahí. En Taregana, Aryabhata estableció un Observatorio Astronómico en el Templo del Sol del siglo VI.
No hay evidencia de que haya nacido fuera de Patliputra y viajado a Magadha, el centro de instrucción, cultura y conocimiento por sus estudios donde incluso estableció un instituto de enseñanza.8 Sin embargo, los primeros textos budistas describen Ashmaka como más al sur, en dakshinapath o el Decán, mientras que otros textos describen que los Ashmakas habían peleado con Alejandro Magno.
Educación
Hay bastante certeza de que, en algún punto, fue a Kusumapura para estudios avanzados y vivió ahí por un tiempo.9 Tanto la tradición hindú como la budista, así comoBhaskara I (629), identifican Kusumapura como Pāṭaliputra, la moderna Patna.6 Un verso menciona que Aryabhata fue el jefe de una institución (kulapati) en Kusumapura y, debido a que la universidad de Nalanda estaba en Pataliputra en ese tiempo y tenía un observatoria astronómico, se especula que Aryabhata puede haber sido también el jefe de la universidad de Nalanda.6 Aryabhata también tiene la reputación de haber establecido un observatorio en el templo del Sol en Taregana, Bihar.10
Otras hipótesis
Alguna evidencia arqueológica sugiere que Aryabhata pudo haber tenido origen en el actual Kodungallur que fue la ciudad capital histórica de Thiruvanchikkulam del antiguo Kerala.11 Por ejemplo, una hipótesis fue que aśmaka (sánscrito para "rocoso, pétreo") puede ser la región en Kerala que ahora es conocida como Koṭuṅṅallūr, basado en la creencia de que se conocía anteriormente como Koṭum-Kal-l-ūr ("ciudad de piedras duras"); sin embargo, viejos registros muestran que la ciudad era de hecho Koṭum-kol-ūr ("ciudad de gobernanza estricta"). De manera similar, el hecho de que varios comentarios en la Aryabhatiya han venido desde Kerala fue usado para sugerir que fue el lugar principal de vida y actividad de Aryabhata; sin embargo, muchos comentarios han venido de fuera de Kerala.
Aryabhata menciona "Lanka" en muchas ocasiones en el Aryabhatiya, pero su "Lanka" es una abstracción, ocupando un punto en el ecuador a la misma longitud que suUjjain.12
Obra
Aryabhata es el autor de varios tratados en matemáticas y astronomía, algunos de los cuales están perdidos. Su mayor trabajo, Aryabhatiya, un compendio de matemáticas y astronomía, fue referido de manera extensa en la literatura matemática de la India y ha sobrevivido a los tiempos modernos. La parte matemática delAryabhatiya cubre aritmética, álgebra, trigonometría plana, y trigonometría esférica. También contiene fracciones continuas, ecuaciones cuadráticas, sumas de series de potencias, y una tabla de senos.
El Arya-siddhanta, un trabajo grande sobre cálculos astronómicos, es conocido a través de los escritos del contemporáneo de Aryabhata, Varaja Mijira, y posteriores matemáticos y comentaristas, incluyendo a Brahmagupta y Bhaskara I. Este trabajo parece estar basado en el más viejo Suria-siddhanta y usa el cálculo del mediodía-noche, en contraposición a la salida del sol en Aryabhatiya. También contenía una descripción de varios instrumentos astronómicos: el gnomon (shanku-iantra), un instrumento de sombras (chhAyA-iantra), posiblemente dispositivos para medir ángulos, semicírculos y círculos (dhanur-iantra / chakra-iantra), un palo cilíndricoiasti-iantra, un dispositivo en forma de sombrilla llamado chhatra-iantra, y relojes de agua de al menos dos tipos, en forma de flecha y cilíndricos.8
Un tercer texto, el cual puede haber sobrevivido en la traducción árabe, es Al ntf o Al-nanf. Afirma ser una traducción de Aryabhata, pero el nombre en sánscrito de este trabajo no es conocido. Probablemente datado del siglo IX, es mencionado por el erudito persa y cronista de la India, Al-Biruni.8
Aryabhatiya
Los detalles directos del trabajo de Aryabhata son conocidos únicamente a partir del Aryabhatiya. Este nombre le fue fue dado a esta obra por comentaristas posteriores. El propio Aryabhata podría no haberle dado un nombre. Su discípulo Bhaskara I lo llama Aśmakatantra (o el tratado de los aśmaka o ashmaka). Es también ocasionalmente referido como Aryaśatasaṣṭa (literalmente, los 108 de Aryabhata), debido a que hay 108 versos en el texto. Está escrito en el estilo lacónico típico de la literatura sutra, en la cual cada línea es una ayuda a la memoria para un sistema complejo. Así, la explicación del significado es debida a comentaristas. El texto consiste en 108 versos y 13 versos introductorios, y está dividido en cuatro pādas o capítulos:
- Gitikapada: (13 versos): grandes unidades de tiempo (kalpa, manvantra, y yuga) los cuales presentan una cosmología diferente a textos anteriores como elVedanga Jyotisha de Lagadha's (c. siglo I a. C.). Hay también una tabla de senos (jya), dada en un único verso. La duración de las revoluciones planetarias durante un mahayuga está dada como 4,32 millones de años.
- Ganitapada (33 versos): cubriendo medición (kṣetra vyāvahāra), aritmética y progresiones geométricas, gnomon/sombras (śankuchāyā), ecuaciones simples, cuadráticas, simultáneas, y indeterminadas.
- Kalakriyapada (25 versos): diferentes unidades de tiempo y un método para determinar las posiciones de los planetas para un día dado, cálculos relacionados con el mes bisiesto (adhikamāsa), kṣayatithis, y una semana de siete días con nombres para los días de la semana.
- Golapada (50 versos): Aspectos geométricos/trigonométricos de la esfera celeste, características de la eclíptica, el ecuador celeste, nodo, forma de la Tierra, la causa del día y la noche, la subida de los signos zodiacales en el horizonte, etc. Además, algunas versiones citan algunos colofones añadidos al final, ensalzando las virtudes del trabajo, etc.
El Aryabhatiya presentó un número de innovaciones en matemáticas y astronomía en forma de verso, las cuales fueron influyentes durante muchos siglos. La extrema brevedad del texto fue expkicada en detalle en comentarios de su discípulo Bhaskara I (Bhashya, c. 600) y por Nilakantha Somayaji en su Aryabhatiya Bhasya (1465). Fue no solamente el primero en encontrar el radio de la Tierra, sino que fue el único en los tiempos antiguos, incluyendo a los griegos y romanos, en encontrar el volumen de la Tierra.
Matemáticas
Sistema de notación posicional y el cero
El sistema de notación posicional, visto por primera vez en el Manuscrito Bakhshali del siglo III, estaba claramente dentro de su obra. Mientras que él no utilizaba un símbolo para el cero, el matemático francés Georges Ifrah explica que el conocimiento del cero estaba implícito en el sistema de notación posicional de Aryabhata como un marcador de posición para las potencias de diez con coeficientes nulos.13
Sin embargo, Aryabhata no utilizó la numeración brahmi. Continuando con la tradición sánscrita del periodo védico, utilizó las letras del alfabeto para denotar números, expresando cantidades, tales como la tabla de senos en una forma in a mnemotécnica.14
Aproximación de π
Aryabhata trabajó en la aproximación del número π, y puede haber llegado a la conclusión de que  es irracional. En la segunda parte del Aryabhatiyam (gaṇitapāda 10), él escribe:
es irracional. En la segunda parte del Aryabhatiyam (gaṇitapāda 10), él escribe:
 es irracional. En la segunda parte del Aryabhatiyam (gaṇitapāda 10), él escribe:
es irracional. En la segunda parte del Aryabhatiyam (gaṇitapāda 10), él escribe:
Esto implica que la relación entre la circunferencia y el diámetro es ((4 + 100) × 8 + 62000)/20000 = 62832/20000 = 3,1416, lo que es exacto hasta cinco cifras significativas.
Se especula que Aryabhata utilizó la palabra āsanna (aproximación), para indicar que no solo es esto una aproximación sino que el valor es inconmensurable (o irracional). Si esto es correcto, es una comprensión bastante sofisticada, debido a que la irracionalidad de pi fue probada en Europa solo hasta 1761 por Johann Heinrich Lambert.16
Después de que Aryabhatiya fuera traducido al árabe (c. 820) esta aproximación fue mencionada en el libro de Al-Juarismi sobre álgebra.8
Trigonometría
En Ganitapada 6, Aryabhata da el área de un triángulo como
- tribhujasya phalashariram samadalakoti bhujardhasamvargah
que se traduce como: "para un triángulo, el resultado de una perpendicular con el semi-lado es el área."17
Aryabhata discutió el concepto de seno en su obra con el nombre de ardha-jya, que literalmente significa "medio-acorde". por simplicidad, la gente comenzó llamándolo jya. Cuando los escritores árabes tradujeron sus obras del sánscrito al árabe, ellos lo refirieron como jiba. Sin embargo, en los escritos árabes las vocales se omiten, y fue escrito simplemente como <jb>. Posteriormente los escritores lo sustituyeron como con jaib, que significa "bolsillo" o "doblez" (en una prenda); en árabe,jiba es una palabra sin significado. Después en el siglo XII, cuando Gerardo de Cremona tradujo estos escritos del árabe al latín, reemplazó el jaib árabe con su contraparte latina, sinus, que significa "curva" o "cavidad". El código alfabético ha sido usado por él para definir un conjunto de incrementos. Si se usa la tabla de Aryabhata y se calcula el valor de sin(30) (correspondiente a hasjha) el cual es 1719/3438 = 0,5, el valor es correcto. Su código alfabético es comúnmente conocido como la cifra de Aryabhata.18
Ecuaciones indeterminadas
Un problema de gran interés para los matemáticos de la India desde tiempos antiguos ha sido encontrar soluciones enteras a ecuaciones que tienen la forma ax + by = c, un tema que ha llegado a ser conocido como ecuaciones diofánticas. Esto es un ejemplo del comentario de Bhāskara sobre Aryabhatiya:
- Encontrar el número que da 5 como el residuo cuando es dividido por 8, 4 como el residuo cuando es dividido por 9, y 1 como el residuo cuando es dividido por 7
Esto es, encontrar N = 8x+5 = 9y+4 = 7z+1. Resulta que el valor más pequeño para N es 85. En general, las ecuaciones diofánticas pueden ser notablemente difíciles. Fueron discutidas de manera extensa en los antiguos textos védicos Shulba-sutras, cuyos fragmentos más antiguos pueden datar desde 800 a. C. El método de Aryabhata para resolver tales problemas es llamado el método kuṭṭaka (कुट्टक). Kuttaka significa "pulverizar" o "romper en pequeñas piezas", y el método involucra un algoritmo recursivo para escribir los factores originales en números más pequeños. Actualmente este algoritmo, elaborado por Bhaskara en 621, es el método estándar para resolver ecuaciones diofánticas de primer orden y es a veces referido como el algoritmo de Aryabhata.19 Las ecuaciones diofánticas son de interés en criptología, y la Conferencia RSA 2006, se concentró en el método kuttaka y el trabajo previo en los Shulba-sutras.
Álgebra
En Aryabhatiya Aryabhata proveyó resultados elegantes para la suma de series matemáticas de cuadrados y cubos:20
y
Astronomía
El sistema de Aryabhata de astronomía fue llamado el sistema audAyaka, en el cual los días son contados a partir de uday, comenzando en lanka o "ecuador". Algunos de sus posteriores escritos en astronomía, los cuales aparentemente proponían un segundo modelo (o ardha-rAtrikA, medianoche) están perdidos pero pueden ser parcialmente reconstruidos a partir de la discusión en el khanDakhAdyaka de Brahmagupta. En algunos textos, parece atribuir los movimientos aparentes del cielo a larotación de la Tierra. Él puede haber creído que las órbitas del planeta son elípticas en vez de circulares.21 22
Movimientos del Sistema Solar
Aryabhata correctamente insistió en que la Tierra rota sobre su eje diariamente, y que el movimiento aparente de las estrellas es un movimiento relativo causado por la rotación de la Tierra, de manera contraria al punto de vista prevaleciente entonces en otras partes del mundo, que era el cielo el que rotaba. Esto se indica en el primer capítulo del Aryabhatiya, donde da el número de rotaciones de la Tierra en un yuga,23 y lo hizo más explícito en su capítulo gola:24
Aryabhata describió un modelo geocéntrico del Sistema Solar, en el cual el Sol y la Luna son cada uno transportados por epiciclos. Ellos a su vez giran alrededor de la Tierra. En este modelo, el cual se encuentra también en el Paitāmahasiddhānta (c. 425), los movimientos de los planetas son cada uno gobernados por dos epiciclos, uno más pequeño manda (lento) y uno más grande śīghra (rápido). 25 El orden de los planetas en términos de distancia desde la Tierra es tomado como: la Luna,Mercurio, Venus, el Sol, Marte, Júpiter, Saturno, y el asterismo."8
Las posiciones y los periodos de los planetas fueron calculados de manera relativa a puntos moviéndose uniformemente. En el caso de Mercurio y Venus, se mueven alrededor de la Tierra a la misma velocidad media que el Sol. En el caso de Marte, Júpiter y Saturno, ellos se movían alrededor de la Tierra a velocidades específicas, representando el movimiento de cada planeta a través del zodiaco. La mayoría de los historiadores de astronomía consideran que este modelo de dos epiciclos refleja elementos de la astronomía en la Antigua Grecia pre-Ptolomeica.26 Otro elemento en el modelo de Aryabhata, el śīghrocca, el periodo planetario básico en relación al Sol, es visto por algunos historiadores como una señal de un subyacente modelo heliocéntrico.27
Eclipses
Los eclipses solares y lunares fueron explicados científicamente por Aryabhata. Aryabhata afirmó que la Luna y los planetas brillan mediante la luz solar reflejada. En vez de la cosmogonía prevaleciente en la cual los eclipses eran causados por los nodos pseudo-planetarios Rajú y Ketu, él explica los eclipses en términos de sombras proyectadas sobre la Tierra. Así, el eclipse lunar ocurre cuando la Luna entra en la sombra de la Tierra (verso gola.37). Él analiza en detalle el tamaño y el alcance de la sombra de la Tierra (versos gola.38–48) y entonces provee los cálculos y el tamaño de la parte eclipsada durante un eclipse. Posteriormente astrónomos hindúes mejoraron los cálculos, pero los métodos de Aryabhata proporcionaron lo esencial. Su pardigma computacional fue tan preciso que el científico del siglo XVIIIGuillaume Le Gentil, durante una visita a Pondicherry, India, encontró que los cálculos hindúes de la duración del eclipse lunar del 30 de agosto de 1765 eran cortos por 41 segundos, mientras que sus gráficas (por Tobias Mayer, 1752) eran largos por 68 segundos.8
Periodos siderales
En unidades modernas de tiempo, Aryabhata calculó la rotación sideral (la rotación de la Tierra con referencia las estrellas fijas) como 23 horas, 56 minutos, y 4.1 segundos;28 el valor moderno es 23:56:4091. De manera similar, su valor para la longitud del año sidéreo en 365 días, 6 horas, 12 minutos, y 30 segundos (365,25858 días)29 tiene un error de 3 minutos y 20 segundos sobre la longitud de un año (365,25636 días).30
Heliocentrismo
Como ha sido mencionado, Aryabhata defendió un modelo astronómico en el cual la Tierra gira sobre su propio eje. Su modelo también dio correcciones (la anomalíaśīgra) para las velocidades de los planetas en el cielo en términos de la velocidad media del Sol. Así, ha sido sugerido que los cálculos de Aryabhata estaban basados en un subyacente modelo heliocéntrico, en el cual los planetas orbitan alrededor del Sol,31 32 33 aunque esto ha sido rebatido.34
También se ha sugerido que aspectos del sistema de Aryabhata pueden haber sido derivados de un modelo heliocéntrico anterior, probablemente griego pretolemeico, el cual era desconocido para los astrónomos hindúes,35 aunque la evidencia es escasa.36 El consenso general es que una anomalía sinódica (dependiente de la posición del Sol) no implica una órbita heliocéntrica físicamente (estando tales correcciones presentes también en posteriores textos astronómicos babilónicos), y que el sistema de Aryabhata no era explícitamente heliocéntrico.37
Legado
La obra de Aryabhata fue de gran influencia en la tradición astronómica de la India e influenció a varias culturas vecinas mediante traducciones. La traducción árabe durante la Edad de Oro del islam (c. 820), fue influenciada de manera particular. Algunos de sus resultados son citados por Al-Juarismi y en el siglo X Al-Biruni afirmó que los seguidores de Aryabhata creían que la Tierra rotaba sobre su propio eje.
Sus definiciones de seno (yia), coseno (koyia), verseno (utkrama-yia), y seno inverso (otkram-yia) influyeron en el nacimiento de la trigonometría. Él fue también el primero en especificar tablas de seno y verseno (1 − cos x), en intervalos de 3.75° desde 0° a 90°, con una precisión de 4 cifras decimales.
De hecho, los nombres modernos "seno" y "coseno" son transcripciones erradas de las palabras jya y kojyaintroducidas por Aryabhata. Como ha sido mencionado, fueron traducidas como jiba y kojiba en árabe y malentendidas por Gerardo de Cremona mientras traducía un texto árabe de geometría al latín. Él asumió que jibaera la palabra árabe jaib, que significa "doblez en una prenda", L. sinus (c. 1150).38
Los métodos de cálculo astronómico de Aryabhata eran también muy influyentes. Junto con las tablas trigonométricas, llegaron a ser ampliamente utilizados en el mundo islámico y fueron utilizados para computar muchas tablas astronómicas árabes (zij). En particular, las tablas astronómicas en el trabajo del científico de laEspaña árabe Azarquiel (siglo XI) se habían traducido al latín como las Tablas de Toledo (s. XII) y permanecieron como las efemérides más precisas utilizadas en Europa por siglos.
Los cálculos de calendarios ideados por Aryabhata y sus seguidores han sido de uso continuo en India para los propósitos prácticos de ajustar el Panchangam (elcalendario hindú). En el mundo islámico, formaron la base del calendario jalali introducido en 1073 por un grupo de astrónomos incluyendo a Omar Jayam,39 versiones las cuales (modificadas en 1925) son los calendarios nacionales en uso actualmente en Irán y Afganistán. Las fechas del calendario jalali están basadas en el tránsito solar actual, como en los calendarios de Aryabhata y anteriores calendarios Siddhanta. Este tipo de calendario requiere una efeméride para calcular las fechas. Aunque las fechas eran difíciles de calcular, los errores estacionales eran menores en el calendario jalali que en el calendario gregoriano.
El primer satélite artificial de la India, el satélite Aryabhata, y el cráter lunar Aryabhata son nombrados así en su honor. Un instituto para la realización de investigaciones en astronomía, astrofísica y ciencias atmosféricas es el Aryabhatta Research Institute of Observational Sciences (ARIOS) cerca de Nainital, India. La competición interescolar Aryabhata Maths Competition es también nombrada en su honor,40 así como el Bacillus aryabhata, una especie de bacteria descubierta por científicos de la Agencia India de Investigación Espacial en 2009.
Aryabhata, el más antiguo de los matemáticos hindúes cuyos trabajos se conservan, nació en el 476, en un lugar que desconocemos. Su obra más importante, llamada por la posteridad Aryabhatiya, es un libro en verso organizado en cuatro capítulos en el que se habla de muy diversos temas de astronomía y matemáticas. En él aparecen aportaciones propias del autor, y también se recogen y sistematizan resultados procedentes de los Siddhantas (una colección de textos donde teorías astronómicas de origen griego aparecen mezcladas con viejas creencias hindúes) y de obras ce científicos anteriores. Así, aunque el Aryabhatiya carece del orden expositivo de los Elementos, el papel de Aryabhata en la matemática India recuerda al de Euclides en la griega, porque de los escritos de los matemáticos anteriores solo han sobrevivido pequeños fragmentos.
El método de inversión para resolver ecuaciones algebraicas
En el Aryabhatiya aparecen algunas ecuaciones algebraicas resueltas por el método de inversión, que consiste en partir del resultado e ir haciendo las operaciones inversas en sentido contrario a como se dan en el enunciado. Una de ellas es la siguiente:
Se multiplica un número por 3, al producto se le suman sus tres cuartas partes, la suma se divide por 7, del cociente se resta su tercera parte, la diferencia se multiplica por sí misma, al cuadrado se le resta 52, de la diferencia se extrae la raíz cuadrada, a la cual se la suma 8, dicha suma se divide por 10 y el resultado es finalmente 2. ¿Cuál es ese número?
Entonces se procede de la siguiente manera: Si la última operación antes de llegar a 2 es dividir por 10, multiplicamos 2 por 10: 2 x 10 = 20. La penúltima operación consistió en sumar 8, entonces restamos 8: 20 - 8 = 12. La antepenúltima consistió en una raíz cuadrada, luego calculamos el cuadrado de lo que tenemos: 122 = 144. Antes de hacer la raíz se restó 52, que es lo que se ha de sumar ahora: 144 + 52 = 196. Antes de restar 52 se hizo un cuadrado, entonces se ha de hacer ahora una raíz cuadrada: √196 = 14. Previamente a la raíz, se había sustraído de una cantidad su tercera parte, lo cual equivale a multiplicarla por dos tercios, entonces multiplicamos por tres medios: 14 x (3/2) = 21. La cantidad multiplicada por tres medios era el resultado de dividir algo entre 7, por consiguiente se ha de multiplicar el último resultado por 7: 21 x 7 = 147. Lo que se había dividido entre 7 es el triple del número buscado al cual se le había sumado sus tres cuartas partes, lo cual equivale a multiplicar por siete cuartos, entonces hay que multiplicar ahora por cuatro séptimos y dividir por 3: (147 x (4/7)) / 3 = 28.
El método de pulverización para resolver ecuaciones diofánticas
Los matemáticos hindúes resolvieron las ecuaciones diofánticas lineales según un procedimiento llamado kuttaka, palabra sánscrita que se podría traducir porpulverización. Vamos a describir el método a través del siguiente ejemplo:
29x + 4 = 8y
Dividimos el coeficiente mayor entre el menor: 29 = 8 x 3 + 5, y hacemos el cambio y = 3x + u, lo que da lugar a una nueva ecuación 5x + 4 = 8u.
Volvemos a dividir el coeficiente mayor entre el menor: 8 = 5 x 1 + 3, y hacemos x = u + v, y tenemos una tercera ecuación 5v + 4 = 3u.
La tercera división es 5 = 3 x 1 + 2, hacemos u = v + w, y tenemos una cuarta ecuación 2v + 4 = 3w.
La cuarta división es 3 = 2 x 1 + 1. Hacemos v = w + t, y tenemos una quinta ecuación 2t + 4 = w.
El coeficiente de una de las incógnitas es 1, entonces damos la otra un cierto valor y hacemos el camino inverso: si t = 0, entonces w = 4, v = 4, u = 8, x = 12 e y = 44. Si se necesita la solución más pequeña posible, se divide 12 por 8 (el coeficiente de la y) y 44 por 29 (el coeficiente de la x), divisiones que dan lugar a los restos 4 y 15. Estos restos son la solución buscada. En cuanto tenemos una solución particular, es fácil comprobar que las demás proceden de la siguiente fórmula:
x = 4 + 8m
y = 15 + 29m
Sobre progresiones aritméticas
Una progresión aritmética es una sucesión de números cada uno de los cuales se deduce del anterior sumándole un numero fijo d llamado diferencia de la progresión. Entonces, si {a1, a2, a3, ..., an} es una progresión, a2 = a1 + d, y en general ap = a1 + (p-1)d.
Aryabhata tiene algunas consideraciones sobre progresiones aritméticas. En primer lugar, explica cómo sumar m términos consecutivos, multiplicando el número de sumandos por el término central (dando así por sentado que el número de sumandos es impar), y para calcularlo proporciona la siguiente regla:
El número de términos menos uno se divide por dos, se suma el número de términos que preceden, se multiplica el resultado por la diferencia, y al producto se le suma el primer elemento de la progresión.
Si los términos a sumar son ap+1, ap+2, ..., ap+m, el “número de términos que preceden” es p, el elemento central se calcula como sigue:
También explica como calcular el número total de términos cuando se conoce el primero, la suma de todos ellos y la diferencia de la progresión:
Multiplica la suma por ocho veces la diferencia, suma el cuadrado de la distancia entre el doble del primer miembro y la diferencia, haz la raíz cuadrada, resta dos veces el primer término, divide el resultado por la diferencia, suma uno y divide por dos.
En efecto, por lo que se ha visto antes, la suma de todos los elementos de la progresión es (porque ahora m = n y p = 0):
El número n es solución de la ecuación cuadrática:
dn2 + (2a1 - d)n - 2S = 0
Resolviéndola, tenemos la regla de Aryabhata:
La trigonometría del Aryabhatiya
La trigonometría griega trabajaba con las cuerdas de los arcos. La idea del seno, la semicuerda del ángulo doble, es de origen hindú. En el Aryabhatiya se da una tabla de los senos de 24 ángulos, cada uno de los cuales excede al anterior en (3 + 3/4)º. Pero no se utilizaba, como se hace hoy, una circunferencia de radio uno, de manera que su concepto de seno no es idéntico al nuestro, de manera que si R es el radio de la circunferencia, el seno hindú de un ángulo es el seno actual multiplicado por R.
Aryabhata toma como unidad de longitud el minuto de arco. Como da al número el valor de 3.1416, el radio es:
La longitud del radio es aproximadamente 3438 veces la del arco de un minuto. Como valor del seno del ángulo más pequeño de su tabla toma 225, la longitud del arco. El error cometido es insignificante:
Para el cálculo de los demás senos, se sirve de la siguiente fórmula (en la cual α = (3 + 3/4)º):
De este modo:
Y así va completando su tabla.
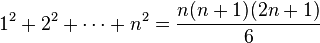
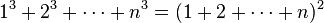

No hay comentarios:
Publicar un comentario