El hexágono regular es un polígono de seis lados y seis ángulos iguales.
Los triángulos formados, al unir el centro con todos los vértices, son equiláteros.
Ángulos de un hexágono
Suma de ángulos interiores de un hexágono = (6 − 2) · 180° = 720°
El valor de un ángulo interior del hexágono regular es 720º/6 = 120º
El ángulo central mide: 360º : 6 = 60º
Diagonales de un hexágono
Número de diagonales = 6 · (6 − 3) : 2 = 9
Apotema del hexágono regular
Perímetro de un hexágono regular
Perímetro = 6 · l
Área de un hexágono regular
Ejemplos
Calcular la apotema, el perímetro y el área de un hexágono regular inscrito en unacircunferencia de 4 cm de radio.
P = 6 · 4 = 24 cm
El área de un cuadrado es 2304 cm². Calcular el área del hexágono regular que tiene su mismo perímetro.
Un hexágono es un polígono de seis lados (L1, L2, L3, L4, L5 y L6). Los lados confluyen dos a dos en seis puntos, llamados vértices.
Elementos del hexágono
En un hexágono se pueden diferenciar los siguientes elementos:
- Vértices (V): puntos en los que confluyen dos lados. Tiene 6 vértices.
- Lados (L): segmentos que unen dos vértices consecutivos del hexágono y que delimitan su perímetro. Tiene 6 lados.
- Diagonal (D): segmento que une dos vértices no consecutivos. En un hexágono convexo hay 9 diagonales (¿por qué hay nueve diagonales?).
- Ángulos interiores (α): ángulo que forman dos lados consecutivos en el vértice en el que confluyen. Hay 6 ángulos interiores. Los ángulos interiores del hexágono suman 720º (¿por qué suman 720º?).
- Ángulos exteriores (β): ángulo formado por un lado con la prolongación exterior del lado consecutivo. Hay 6 ángulos exteriores.
Tipos de hexágono
Según las características de los lados y ángulos del hexágono, se clasifica en dos tipos:
- Hexágono regular: figura geométrica con seis lados y ángulos iguales (todos sus ángulos interiores son de 120º, resultado de dividir 720º entre 6 ángulos).
- Hexágono irregular: figura geométrica cuyos seis lados y ángulos no son iguales entre sí.
Área del hexágono
El cálculo del área de un hexágono es diferente dependiendo de si el hexágono es regular o irregular.
Área del hexágono regular
El área del hexágono regular se calcula como la mitad del producto del perímetro y la apotema (ap). Al ser su perímetro seis veces la longitud (L) de uno de sus lados, el área será:
Área del hexágono irregular
El área del hexágono irregular requiere ser calculada por métodos alternativos de cálculo de áreas. El más común es dividir el hexágono en seis triángulos y calcular el área sumando las seis áreas de los triángulos.
El área del hexágono irregular se puede calcular mediante dos procedimientos alternativos: el método de triangulación o el determinante de Gauss.
Triangulación del hexágono irregular
Sea P un hexágono irregular. Se desea calcular su área (A).
El método de triangulación consiste en dividir el hexágono en figuras más fáciles de calcular el área. En este caso se divide en seis triángulos y el área del hexágono será la suma del área de esos seis triángulos.
- Se divide el hexágono en seis triángulos (T1, T2, T3, T4, T5 y T6) . Estostriángulos cumplen que uno de sus lados es un lado del hexágono y que todos confluyen en un mismo punto interior del hexágono.
- Se miden las alturas (h1, h2,…, h6) de los triángulos. La altura de cada triángulo será el segmento de recta perpendicular al lado del hexágono que va desde ese mismo lado hasta el punto interior.
- Se calculan las áreas de los seis triángulos. El área del primer triángulo es:Utilizamos la misma fórmula para calcular el área de los otros cinco triángulos.
- Sumamos las seis áreas y obtenemos el área del hexágono irregular:
Determinante de Gauss
Un procedimiento muy útil para hallar el área de cualquier polígono irregular es a través del determinante de Gauss.
Supone dibujar la figura sobre un plano cartesiano, fijando las coordenadas de cada uno de los vértices del polígono.
Se elige al azar cualquiera de ellos y se colocan los pares en la siguiente fórmula. Se ha de recorrer el polígono en el sentido contrario al de las agujas del reloj, teniendo en cuenta que el primer par de coordenadas corresponden al vértice elegido y, después de recorrer en sentido antihorario todos los vértices, el último par debe volver a ser el par inicial.
Sean los vértices del hexágono: (x1,y1), (x2,y2),…, (x6,y6). La fórmula es la siguiente:
Resolviéndolo por el procedimiento conocido, habremos hallado rápidamente el área del hexágono irregular.
Este método es aplicable a cualquier polígono con cualquier número de lados, tanto en el caso de polígonos cóncavoscomo en los convexos.
Perímetro del hexágono
La fórmula del perímetro del hexágono es diferente dependiendo si el hexágono es regular o irregular.
Perímetro del hexágono regular
El hexágono regular tiene los seis lados de la misma longitud, por lo que su perímetro es seis veces uno de ellos:
Perímetro del hexágono irregular
Por tanto, su perímetro será la suma de la longitud de sus seis lados.
Propiedades
Un hexágono tiene 6 lados y 9 diagonales, resultado que se puede obtener aplicando la fórmula para determinar el número de diagonales de los polígonos convexos 3 ,  , donde
, donde 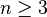 y n representa el número de vértices; siendo el número de vértices
y n representa el número de vértices; siendo el número de vértices  , tenemos:
, tenemos:
 , donde
, donde 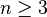 y n representa el número de vértices; siendo el número de vértices
y n representa el número de vértices; siendo el número de vértices  , tenemos:
, tenemos:
La suma de todos los ángulos internos de cualquier hexágono es 720 grados ó 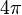 radianes. Se usa la fórmula
radianes. Se usa la fórmula  . O bien la suma de los ángulos internos de un polígono convexo cualquiera es igual a dos rectos (2R = 180º) por el número n de lados menos 2. 4
. O bien la suma de los ángulos internos de un polígono convexo cualquiera es igual a dos rectos (2R = 180º) por el número n de lados menos 2. 4
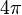 radianes. Se usa la fórmula
radianes. Se usa la fórmula  . O bien la suma de los ángulos internos de un polígono convexo cualquiera es igual a dos rectos (2R = 180º) por el número n de lados menos 2. 4
. O bien la suma de los ángulos internos de un polígono convexo cualquiera es igual a dos rectos (2R = 180º) por el número n de lados menos 2. 4Parhexágono
Siguiendo el hilo de un paralelogramo, un parhexágono o parexágono es aquel hexágono particular, en el que un lado es igual y paralelo a un lado opuesto, pero cada par de estos lados es de diferente tamaño. 5
Proposición
Sea ABCDEF un hexágono irregular cualquiera, se unen A con C; B con D; C con E; D con F; E con A; F con B. Se forman los seis triángulos ABC, BCD, CDE, DEF, EFA, FAB. En cada uno de ellos se localiza su baricentro; que se denotan como A', B', C', D', E', F'. Se unen sucesivamente dichos puntos, el hexágono A'B'C'D'E'F' es un parhexágono.6
Hexágono regular
El hexágono regular es un polígono convexo con seis lados iguales y seis ángulos iguales.
El hexágono regular tiene las siguientes propiedades:
- Sus ángulos internos son congruentes midiendo 120° ó
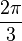 rad. Resultado de
rad. Resultado de 
- Cada ángulo externo del hexágono regular mide 60° ó
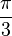 rad.
rad. - Está íntimamente relacionado con los triángulos equiláteros:
- Uniendo cada vértice con su opuesto, el hexágono regular queda dividido en seis triángulos equiláteros.
- Numérense los vértices de 1 a 6 en el sentido horario. Uniendo los vértices impares se obtiene un triángulo equilátero; uniendo los vértices pares se obtiene otro.
- Además de los cuadrados y los triángulos equiláteros, los hexágonos regulares congruentes (o iguales) son los terceros polígonos regulares que se pueden juntar para revestir totalmente una superficie plana sin dejar ningún vano.
- Las seis raíces sextas de 1 o los números complejos que resuelven la ecuación
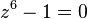 están en los vértices de un hexágono regular ubicado en el plano complejo, siendo el primer vértice el punto (1,0). 7
están en los vértices de un hexágono regular ubicado en el plano complejo, siendo el primer vértice el punto (1,0). 7
- Un hexágono regular es inscriptible y circunscribible en una circunferencia. Caben las igualdades:
-
 , r es el radio del círculo inscrito.
, r es el radio del círculo inscrito.
-
 , R es el radio del círculo circunscrito.
, R es el radio del círculo circunscrito.
- Las perpendiculares trazadas por los puntos medios del hexágono regular y las bisectrices de los ángulos internos del hexágono regular son ejes de simetría del mismo. 9 .
Perímetro
Su perímetro es seis veces la longitud de su lado.
 , donde n es el número de lados y
, donde n es el número de lados y  , la longitud del lado.
, la longitud del lado.
Área
Si se conoce la longitud del apotema a del polígono, una alternativa para calcular el área es:
o
Si sólo conocemos el lado t podemos calcular el área con la siguiente fórmula:
 , que equivale a las áreas de seis triángulos equiláteros que se obtienen al unir el centro con los seis vértices.
, que equivale a las áreas de seis triángulos equiláteros que se obtienen al unir el centro con los seis vértices.
Construcción geométrica
Un hexágono regular puede construirse utilizando únicamente una regla y compás:
- Dado un punto O cualquiera, trazar una circunferencia cuyo radio sea igual al lado del hexágono a construir;
- Elegir un punto A sobre la circunferencia y trazar un diámetro que cruce O y A. Marcar el otro punto donde este diámetro interseca la circunferencia como D;
- Apoyando el compás en el punto A, trazar un arco que cruce O, cortando a la circunferencia en dos puntos, marcados como B yF;
- Apoyando el compás en el punto D, trazar un arco que cruce O, cortando a la circunferencia en dos puntos, marcados como C yE
En la naturaleza

Los panales están construidos con formas hexagonales.
La Francia continental o parte metropolitana de Francia recibe el sobrenombre de Hexágono (l'Hexagone en francés), por tener una forma vagamente hexagonal.




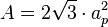


No hay comentarios:
Publicar un comentario