Apuntes de Geometría

polígonos inscritos

Un polígono está inscrito en una circunferencia si todos sus vértices están contenidos en ella.

Todo polígono inscrito es regular.

El centro de un polígono inscrito es el centro de la circunferencia circunscrita en él.

El radio del polígono inscrito es el radio de la circunferencia circunscrita en él.

Polígonos circunscritos

Un polígono está circunscrito en una circunferencia, si todos los sus lados son tangentes a lacircunferencia.

El polígono circunscrito toca en el punto medio de cada lado a la circunferencia inscrita.

El centro de la circunferencia inscrita equidista de todos los lados del polígonocircunscrito.

La apotema del polígono circunscrito es el radio de la circunferencia inscrita.

Lado de un triángulo equilátero inscrito

Calcular el lado de un triángulo equilátero inscrito en una circunferencia de 10 cm de radio.

Lado de un cuadrado inscrito

Calcular el lado de un cuadrado inscrito en una circunferencia de 5 cm de radio.

Apotema del hexágono inscrito

Calcular la apotema de un hexágono inscrito en una circunferencia de 4 cm de radio.

PENTÁGONO INSCRITO EN UNA CIRCUNFERENCIA.

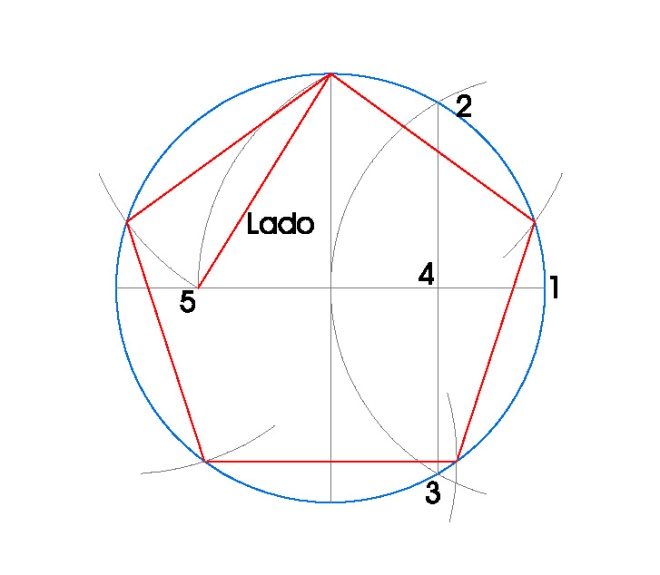
PASOS:

1. Dibujamos la circunferencia en la que vamos a inscribir el pentágono, en nuestro caso de radio 3 cm.
2. Dibujamos sus dos diámetros perpendiculares usando la escuadra y el cartabón.
3. Hacemos centro de compás en el punto 1 con radio 3 cm. y obtenemos los puntos 2 y 3.
4. Uniendo los puntos 2 y 3 obtenemos el punto 4, que es el punto medio del radio de la circunferencia.
5. Hacemos centro de compás en 4 con radio hasta donde el diámetro vertical nos corta a la circunferencia y hacemos un arco, obteniendo 5.
6. Ya hemos obtenido el lado del pentágono inscrito.
7. Tomamos radio de compás el lado del pentágono inscrito y vamos marcando los vértices del pentágono en la circunferencia.
8. Una vez obtenidos los vértices del pentágono, sólo nos queda unirlos.

2. HEXÁGONO INSCRITO EN UNA CIRCUNFERENCIA.

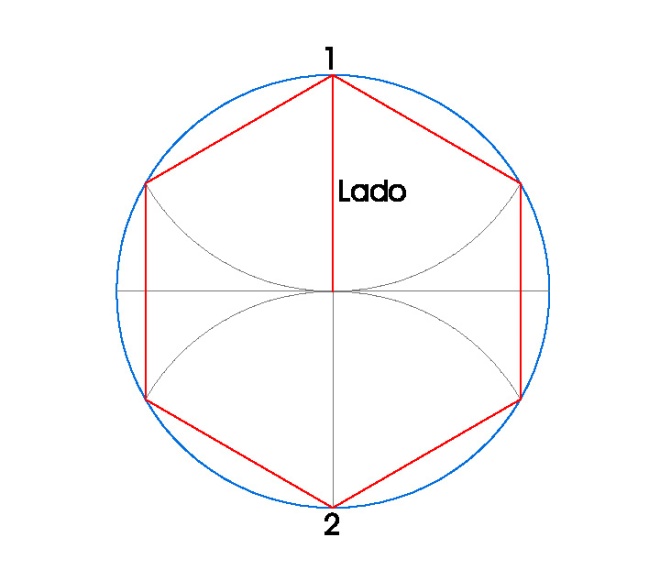
PASOS:

1. Dibujamos la circunferencia en la que vamos a inscribir el hexágono, en nuestro caso de radio 3 cm.
2. Dibujamos sus dos diámetros perpendiculares usando la escuadra y el cartabón.
3. Hacemos centro de compás en el punto 1 con radio 3 cm. y donde ese arco se corta con la circunferencia obtenemos dos vértices del hexágono.
4. Hacemos centro de compás en el punto 2 con radio 3 cm. y donde ese arco se corta con la circunferencia obtenemos otros dos vértices del hexágono.
5. Los otros dos vértices del hexágono son los puntos 1 y 2.
6. Una vez obtenidos los vértices del hexágono, sólo nos queda unirlos.

3. HEPTÁGONO INSCRITO EN UNA CIRCUNFERENCIA.

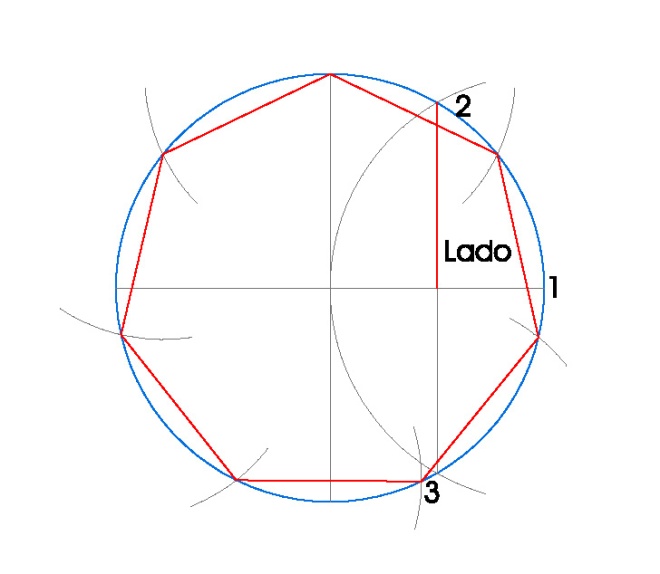
PASOS:

1. Dibujamos la circunferencia en la que vamos a inscribir el heptágono, en nuestro caso de radio 3 cm.
2. Dibujamos sus dos diámetros perpendiculares usando la escuadra y el cartabón.
3. Hacemos centro de compás en el punto 1 con radio 3 cm. y obtenemos los puntos 2 y 3.
4. Uniendo los puntos 2 y 3 obtenemos el lado del heptágono inscrito.
5. Tomamos radio de compás el lado del heptágono inscrito y vamos marcando los vértices del heptágono en la circunferencia.
6. Una vez obtenidos los vértices del heptágono, sólo nos queda unirlos.

4. OCTÓGONO INSCRITO EN UNA CIRCUNFERENCIA.

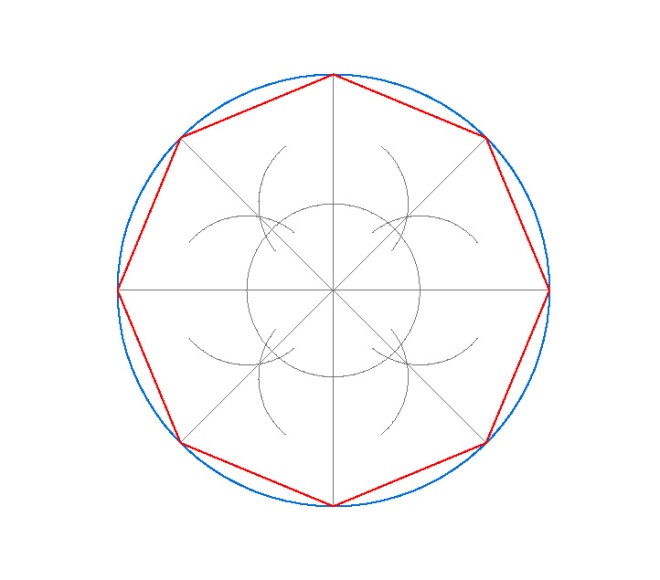
PASOS:

1. Dibujamos la circunferencia en la que vamos a inscribir el pentágono, en nuestro caso de radio 3 cm.
2. Dibujamos sus dos diámetros perpendiculares usando la escuadra y el cartabón.
3. Ya tenemos la circunferencia dividida en 4 partes.
4. Para dividirla en 8 partes, no tenemos más que hacer las bisectrices de los 4 ángulos de 90º en que está dividida la circunferencia.
5. Una vez obtenidos los vértices del octógono, sólo nos queda unirlos.

5. ENEÁGONO INSCRITO EN UNA CIRCUNFERENCIA.

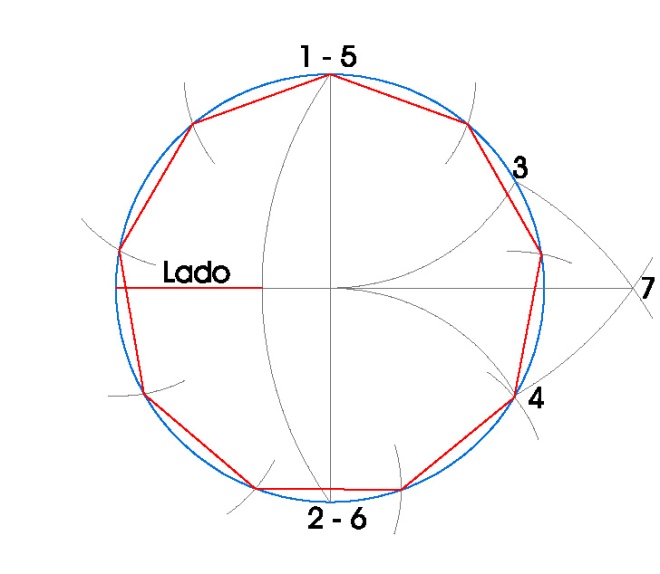
PASOS:

1. Dibujamos la circunferencia en la que vamos a inscribir el pentágono, en nuestro caso de radio 3 cm.
2. Dibujamos sus dos diámetros perpendiculares usando la escuadra y el cartabón.
3. Hacemos centro de compás en el punto 1 con radio 3 cm. y obtenemos el punto 3.
4. Hacemos centro de compás en el punto 2 con radio 3 cm. y obtenemos el punto 4.
5. Hacemos centro de compás en el punto 5 con radio hasta el punto 4 y dibujamos un arco.
6. Hacemos centro de compás en el punto 5 con radio hasta el punto 3 y dibujamos otro arco.
7. Donde esos dos arcos se cortan obtenemos el punto 7.
8. Hacemos centro de compás en el punto 7 con radio hasta el punto 1, que coincide con el 5, y dibujamos un arco.
9. El lado del eneágono inscrito es la distancia que queda desde donde ese arco nos corta al diámetro de la circunferencia hasta la circunferencia.
10. Tomamos radio de compás el lado del eneágono inscrito y vamos marcando los vértices del eneágono en la circunferencia.
11. Una vez obtenidos los vértices del eneágono, sólo nos queda unirlos.

6. DECÁGONO INSCRITO EN UNA CIRCUNFERENCIA.

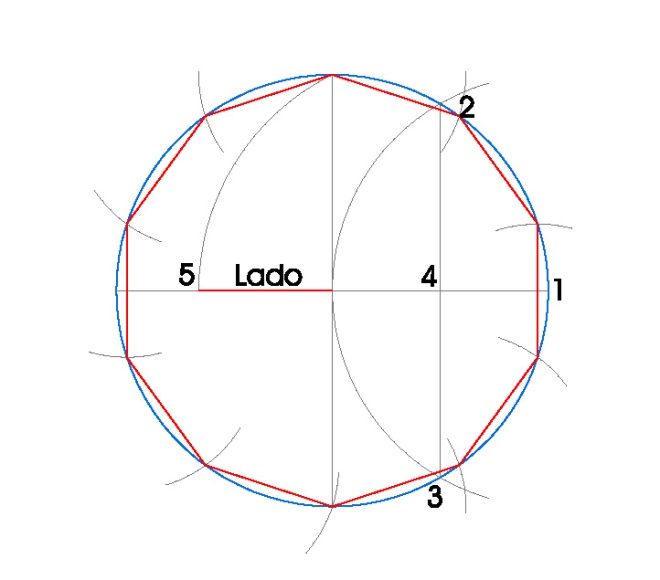
PASOS:

1. Dibujamos la circunferencia en la que vamos a inscribir el decágono, en nuestro caso de radio 3 cm.
2. Dibujamos sus dos diámetros perpendiculares usando la escuadra y el cartabón.
3. Hacemos centro de compás en el punto 1 con radio 3 cm. y obtenemos los puntos 2 y 3.
4. Uniendo los puntos 2 y 3 obtenemos el punto 4, que es el punto medio del radio de la circunferencia.
5. Hacemos centro de compás en 4 con radio hasta donde el diámetro vertical nos corta a la circunferencia y hacemos un arco, obteniendo 5.
6. Él lado del decágono inscrito, es la distancia desde 5 hasta el centro de la circunferencia.
7. Tomamos radio de compás el lado del decágono inscrito y vamos marcando los vértices del decágono en la circunferencia.
8. Una vez obtenidos los vértices del decágono, sólo nos queda unirlos.

Solución de la lámina completa:

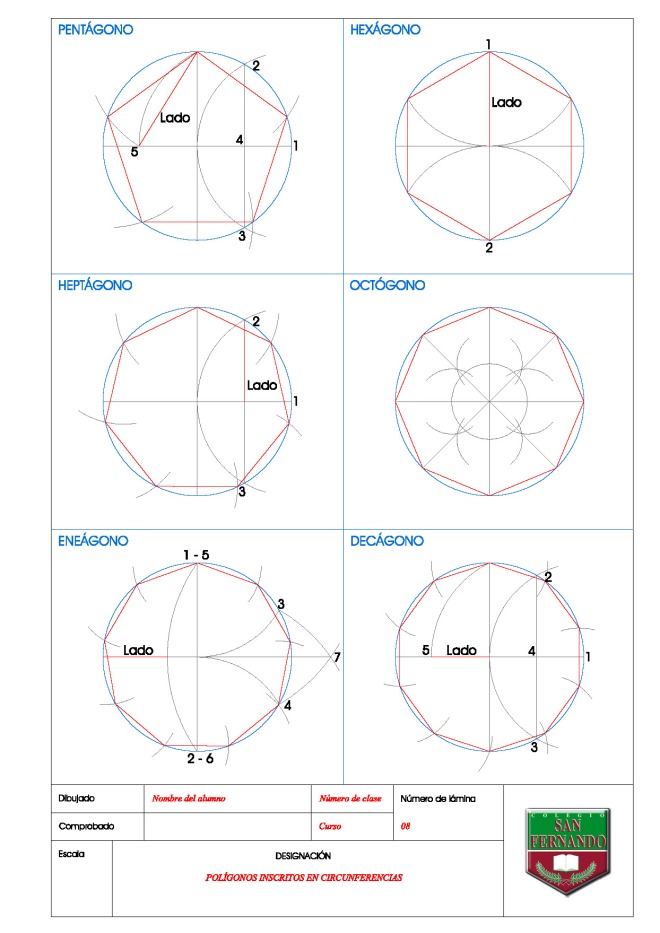
Area de polígonos inscritos en una circunferencia de radio r Ya que es fácil encontrar una fórmula para el área de un polígono regular de n lados, podemos obtener el área del círculo al encontrar el límite de la fórmula cuando n tiende a infinito. Usemos el símbolo P(n) para denotar el área de un polígono regular de nlados inscrito en un círculo de radio r. Para obtener una fórmula para P(n)podemos usar el hecho de que cualquier polígono regular de n lados puede ser cortado en triángulos congruentes y así obtenemos el área del polígono como la suma de las áreas de los triángulos. El área de cada triángulo puede calcularse al multiplicar un medio de su base por su altura. La distancia del centro del círculo a un lado del polígono nos da la longitud de la altura del triángulo, a saber rcos(180º/n). Además, un medio de la base del triángulo, que es la mitad de la longitud del lado del polígono, esrsen(180º/n). Así, el área total de nuestro polígono esta dada por la fórmula: