Apuntes de Geometría

la diagonal

Las diagonales son los segmentos que determinan dos vértices no consecutivos

Número de diagonales de un polígono

Si n es el número de lados de un polígono:

Número de diagonales = n · (n − 3) : 2

4 · (4 − 3) : 2 = 2

5 · (5 − 3) : 2 = 5 6 · (6 − 3) : 2 = 9

Diagonal del cuadrado

Calcular la diagonal de un cuadrado de 5 cm de lado.

Diagonal del rectángulo

Calcular la diagonal de un rectángulo de 10 cm de base y 6 cm de altura.

Las diagonales de un polígono son segmentos que unen dos vértices no consecutivos.

El número de diagonales (D) viene determinado por el número de lados (N) que tiene elpolígono. Su fórmula es:

Ejemplos

Un cuadrado tiene 4 lados. Se aplica la fórmula para comprobar el número de diagonales:

El cuadrado tiene dos diagonales. Si la longitud de los lados son conocidos, se puede calcular la longitud de las diagonales.

Un hexágono tiene 6 costados. Si se aplica la fórmula se puede saber el número de diagonales:

El hexágono tiene 9 diagonales.

Una diagonal es todo segmento que une dos vértices diagonalmente no consecutivos de un polígono o de un poliedro. En sentido coloquial, una diagonal es una recta o segmento con cierta inclinación o un conjunto de elementos alineados de esta manera.

Etimología

La palabra diagonal proviene del griego saco (diagonios), utilizada tanto por Estrabón¹ como por Euclides² para referirse al segmento que conecta dos vértices de un rombo o cuboide,³ y formada por dia- ("a través") y gonia ("ángulo", relacionada agony, "rodilla"), luego adoptada en latín como diagonus ("recta enfocante").

Número de diagonales de un polígono

En un polígono de n lados, el número de diagonales viene dado por la ecuación:

Este resultado se obtiene razonando de la siguiente manera: a partir de cada uno de los n vértices pueden trazarse n - 3 diagonales, pues no hay diagonales hacia sí mismo ni hacia los 2 vértices adyacentes. Dado que la diagonal que va de un vértice A a otro B y la que viene de ese vértice B de regreso al vértice A son la misma diagonal, se divide por dos para evitar contar esta diagonal dos veces

Matriz matemática

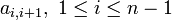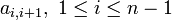Con el mismo criterio, se habla de diagonal secundaria superior o inferior para referirse a los elementos inmediatamente por encima o por debajo, respectivamente, de la diagonal principal. Con la misma definición de A que se dio antes, los elementos  conforman la diagonal secundaria superior, mientras que los elementos  conforman la diagonal secundaria inferior.con el mismo criterio, se habla de un diagonal.

Otros usos del término

Se denomina calle diagonal (o simplemente diagonal) a toda calle que, en un trazado de calles paralelas, una intersecciones rompiendo este esquema. Por extensión una diagonal sirve para referirse a los elementos inmediatamente por encima o por debajo de la diagonal principal.

En un sistema de coordenadas cartesianasse han representado las curvas de algunas raíces, así como de sus potencias, en elintervalo [0,1]. La diagonal, de ecuación y= x, es eje de simetría entre cada curva y la curva de su inversa.

Recuerda que las diagonales del rombo una es mayor que la otra:

Si te fijas bien, dentro del rombo se nos han formado dos triángulos iguales como lo tienes dibujados en la siguiente figura:

La base del triángulo amarillo mide el valor de la diagonal mayor y la altura o anchura máxima vale la mitad de la diagonal menor.

Vemos que el área del rombo se calcula multiplicando las dos diagonales y a ese resultado lo dividimos por 2.

También podemos deducir el área del rombo del modo siguiente:
Si te fijas, en la siguientes figura, tenemos dos triángulos que forman el rombo. Los dos triángulos son iguales.
La altura de cada uno equivale a la mitad de la diagonal mayor y la base, común para ambos triángulos, es igual a la diagonal menor.

15(2).13 Calcula el área que ocupa la parte pintada de rojo en la figura siguiente:

Respuesta: 

Solución
Vamos a resolverlo de dos maneras:
a) Calculamos el área del rectángulo: 

Calculamos el área del rombo: 

La diferencia entre las áreas del rectángulo y el rombo nos dará el área coloreada de rojo: 

b)
Si observas la siguiente figura verás que cada zona pintada de rojo es un triángulo cuyas medidas las tienes indicadas en la misma:

Tienes 4 triángulos de 4,25 cm., de base por 2 cm., de altura, es decir, cada uno tiene una superficie de:

Como son 4 triángulos, la superficie en rojo vale: 

15(2).14 El área de un rombo vale  y la diagonal mayor vale el doble de la diagonal menor. Calcula el valor de las dos diagonales.

Respuesta: 10 m. la mayor y 5 m. la menor.
Solución:
Si el valor de la diagonal menor es: d
El valor de la diagonal mayor será: 2d
Dedujimos que el área del rombo es igual a:

CÁLCULO DEL ÁREA DEL ROMBOIDE.

Recordarás que un romboide es un paralelogramo que tiene sus lados paralelos dos a dos, lo mismo que sus ángulos.
Sus diagonales no son perpendiculares ni son iguales. En la figura siguiente tienes un romboide con sus medidas de líneas y ángulos para que compruebes lo que acabamos de decir:

Para deducir el área del romboide fíjate en la figura siguiente:
Tienes un romboide de 6 cm. de largo de base y 2,5 cm., de alto o ancho.

Si ahora trazamos dos perpendiculares desde los extremos de la línea superior hasta la base:

Vemos que se nos forman dos triángulos rectángulos iguales que los pintamos de rojo:

Si eliminamos el primero de los triángulos y le añadimos el segundo al romboide, su área sigue siendo la misma:

Pero ahora, se ha transformado en un rectángulo cuya área será el largo por el ancho o alto.

Compruebo que el área de un romboide y rectángulo son iguales. En este caso: 

15(2).15 Toma papel, regla, lapicero y tijeras. Dibuja un romboide que tenga 10 cm., de largo y una anchura de 4 cm.

Desde los extremos del lado superior traza las alturas (rectas perpendiculares a la base).
Recorta los triángulos que se te han formado (de color verde en la figura siguiente) y comprueba que los dos triángulos son iguales y que lo que te queda después de recortar es un rectángulo que tiene 10 cm., de largo y 4 cm., de ancho.

Respuesta: