La apotema de un polígono regular es la distancia del centro al punto medio de un lado.
Apotema de un triángulo equilátero
Ejemplo
Calcular la apotema de un triángulo equilátero de 6 cm de lado.
Apotema de un cuadrado
Ejemplo
Calcular la apotema de un cuadrado de 6 cm de lado.
a = 6/2 = 3 cm
Apotema de un pentágono regular
Esta fórmula permite calcular la apotema de cualquier polígono regular.
Ejemplo
Calcular la apotema de un pentágono regular de 6 cm de lado.
Apotema de un hexágono regular
Ejemplo
Hallar la apotema de un hexágono regular inscrito en una circunferencia de 4 cm de radio.
Cálculo de la apotema lateral de una pirámide:
Calculamos la apotema lateral de la pirámide, conociendo la altura y la apotema de la base, aplicando el teorema de Pitágoras en el triángulo sombreado:
Cálculo de la apotema lateral de un tronco de pirámide:
Calculamos la apotema lateral del tronco pirámide, conociendo la altura, la apotema de la base mayor y apotema de la base menor, aplicando el teorema de Pitágoras en el triángulo sombreado:
Cálculo de la arista lateral de una pirámide
Calculamos la arista lateral de la pirámide, conociendo la altura y el radio de la base o radio de la circunferencia circunscrita, aplicando el teorema de Pitágoras en el triángulo sombreado:
Para calcular el área total de una pirámide tendremos que conocer dos medidas, la arista lateral y la arista de la base.
Si la base es un polígono regular de n lados, tendrá n triángulos isósceles que forman la superficie lateral según vimos en el desarrollo de las pirámides. Estos triángulos tienen de base la arista de la base y de altura la apotema de la pirámide, ap, que se puede calcular fácilmente, ya que es la altura de un triángulo isósceles del que se conocen los lados.
El área lateral de la pirámide se calcula multiplicando un medio del perímetro de la base por la apotema.
Para saber el área total deberemos sumar al área lateral el área de la base.
Ejercicios resueltos
1. Halla el área total de la siguiente pirámide cuadrangular.
2. Halla el área total de una pirámide hexagonal regular con aristas laterales de 13 cm y aristas de la base de 10 cm.
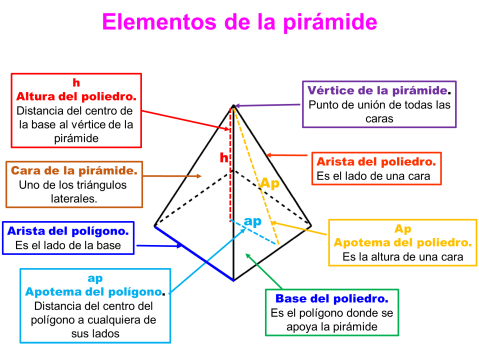
Para calcular el área total de una pirámide es necesario conocer:
- El área de la base (áb ), que es el polígono donde se apoya la pirámide.
- El perímetro de la base(pb ), que es la longitud de todas las caras.
- La apotema de la base (ap), que es la distancia del centro de la base a cualquier lado.
- La apotema de la pirámide (Ap), que es la altura de una cara lateral.
- La altura del poliedro (h), que es la distancia que hay del centro de la base al vértice de la pirámide.
Si deseas el formulario para obtener el volumen haz clic aquí
Las fórmulas generales para obtener el área y el volumen de una pirámide son las siguientes:
Ejemplos de ejercicios de área y volumen de una pirámide.
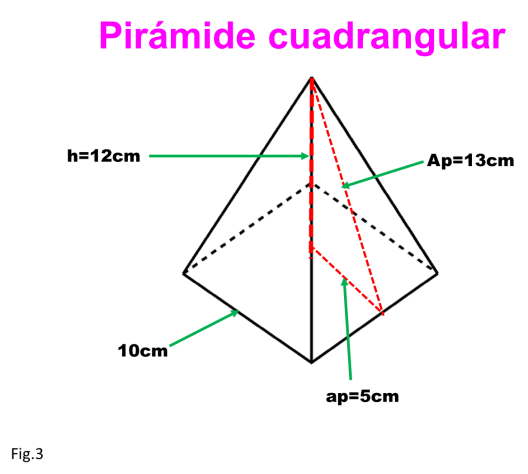
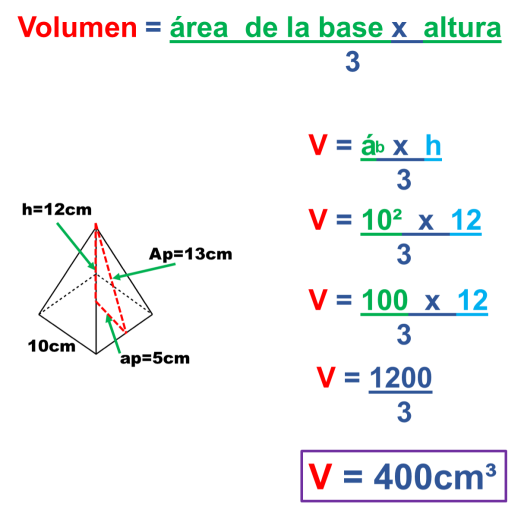
1.- Hallar el área total y el volumen de una pirámide cuadrangular cuya arista de la base mide 10, la altura de 12 cm y un Apotema del poliedro de 13 cm.
Nos enfocamos en la forma de la base de la pirámide para despejar estas fórmulas. El problema
indica que es una pirámide cuadrangular con las siguientes medidas:
Obtengamos primero el área lateral (el de las cuatro caras triangulares) que es el área coloreada.
Ver vídeo (Para recordar cómo se obtiene el área de un triángulo).
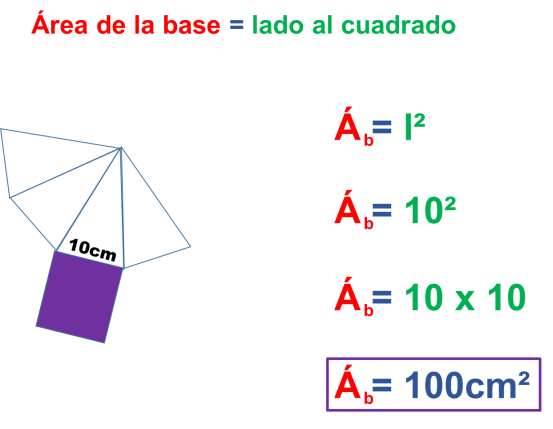
Y ahora el área de la base. Para ello en la fórmula general vamos a sustituir por la fórmula para obtener el área de un cuadrado, ya que la base es cuadrangular. Es el área coloreada.
Ver vídeo (Para recordar cómo se obtiene el área de un cuadrado).
Por último sumamos los valores del área lateral y del área de la base para obtener el área total de la pirámide cuadrangular especificada.
Ahora obtenemos el volumen de la pirámide cuadrangular sustituyendo la fórmula del área de la base por la del área del cuadrado y multiplicando por la altura del poliedro.
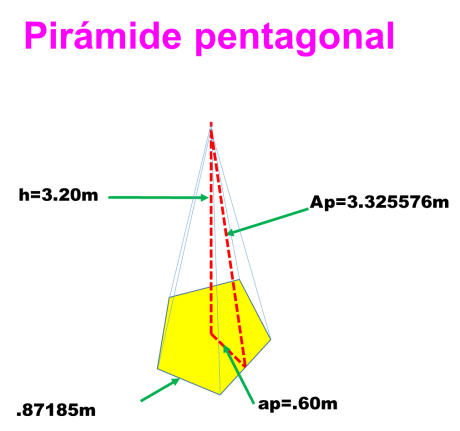
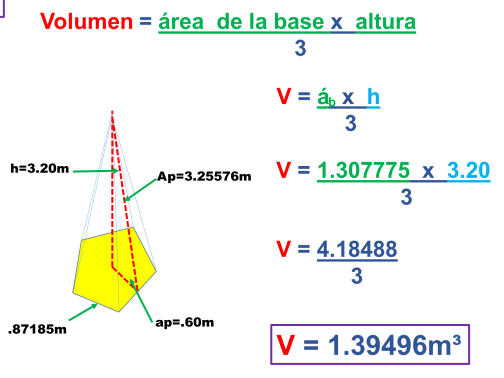
2.- Hallar el área total y el volumen de una pirámide regular pentagonal cuya altura mide 3.20m, el lado de la base 0.87185m, el apotema del poliedro 3.25576m; y el apotema de la base 0.60m
Nos enfocamos en la forma de la base de la pirámide para despejar estas fórmulas. El problema indica que es una pirámide pentagonal con las siguientes medidas.
Obtengamos primero el área lateral (el de las cinco caras triangulares) que es el área coloreada.
Ver vídeo (Para recordar cómo se obtiene el área de un triángulo).
Y ahora el área de la base. Para ello en la fórmula general vamos a sustituir por la fórmula para obtener el área de un pentágono regular, ya que la base es pentágono. Es el área coloreada.
Por último sumamos los valores del área lateral y del área de la base para obtener el área total de la pirámide pentagonal especificada.
Ahora obtenemos el volumen de la pirámide pentagonal sustituyendo la fórmula del área de la base por la del área del pentágono y multiplicando por la altura del poliedro.
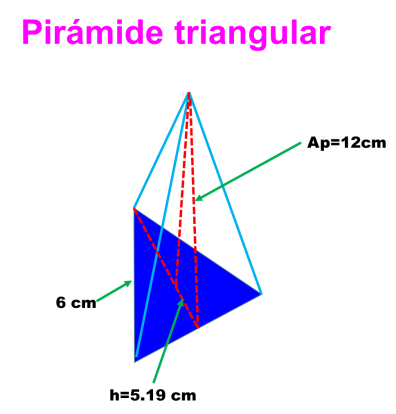
3.- Hallar el área total y el volumen de una pirámide regular triangular cuyas medidas son las siguientes:
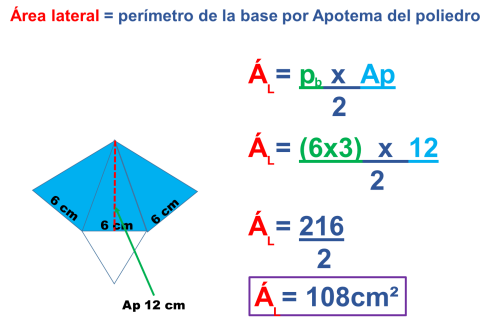
Obtengamos primero el área lateral (el de las cinco caras triangulares) que es el área coloreada.
Recuerda que en una pirámide regular la altura de cada uno de los triángulos laterales (caras), llamada apotema del poliedro, es igual a la altura de la pirámide.
Ver vídeo (Para recordar cómo se obtiene el área de un triángulo).
Y ahora el área de la base. Para ello en la fórmula general vamos a sustituir por la fórmula para obtener el área de un triángulo, ya que la base es un triángulo equilátero. Es el área coloreada.
Por último sumamos los valores del área lateral y del área de la base para obtener el área total de la pirámide regular triangular especificada.
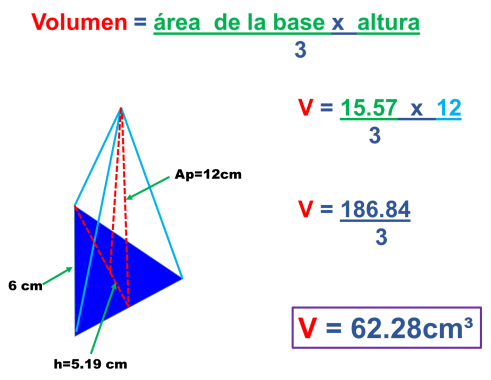
Ahora obtenemos el volumen de la pirámide triangular sustituyendo la fórmula del área de la base por la del área del triángulo y multiplicando por la altura del poliedro.

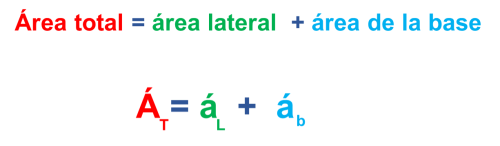







No hay comentarios:
Publicar un comentario