espacio proyectivo complejo al espacio de las líneas complejas de Cn+1 que pasan por el origen. Normalmente se nota por P(Cn+1), Pn(C) o CPn
Constituye una variedad compleja compacta de dimensión compleja n definida identificando los puntos proporcionales de Cn+1-{0} mediante la siguiente relación de equivalencia:
Topología
Sea la proyección que lleva cada z en su clase de equivalencia. Dotamos a CPn de la topología cociente, de modo que es abierto si y sólo si lo es. Esta topología convierte a la proyección en una aplicación continua.- CPn es compacto y conexo
Para ello basta observar que es imagen por una aplicación continua de la esfera real S2n+1. En concreto por la composición de aplicaciones dada por- ,
Esta aplicación es sobreyectiva pues toda línea pasa por un punto de S2n+1.Estructura compleja
Podemos construir un atlas mediante las cartas definidas por:donde por ^ debemos entender que no aparece la entrada correspondiente.Si , se comprueba que el cambio de cartas es holomorfo.Subespacios lineales de CPn
Toda inclusión del tipo Ck+1 → Cn+1 induce una inclusión entre los proyectivos correspondientes CPk → CPn. A la imagen de esta aplicación se le denomina subespacio lineal de CPn.Si k = n-1, a la imagen de esta aplicación se le denomina hiperplano de CPn. Si k = 1, de su imagen se dice que es una línea del mismo.- homología es una transformación homográfica resultante de efectuar una proyección desde un punto, en la que a cada uno de los puntos de una figura plana le corresponden, respectivamente, un punto de su figura homóloga, cumpliéndose que:
- Un punto P y su imagen P' siempre están alineados con un punto llamado centro de la homología (O). El centro de homología es invariante.
- La imagen de una recta R es otra recta R'.
- Una recta R y su imagen R' siempre se cortan sobre una recta llamada eje de homología (e). Cada punto sobre esta recta es invariante. Se denomina a ese punto punto doble de la recta R.
- La incidencia se preserva. Por ejemplo si dos rectas R y S se cortan en un punto P, sus imágenes R' y S' se cortarán en la imagen del punto P P'.
Determinación imágenes de puntos en un sistema de homología
Para determinar la imagen Q' de un punto Q del plano, nos bastaremos de ese par de puntos P y P' que tenemos originalmente. Trazamos una recta PQ, que tendrá un punto doble sobre el eje de homología. La imagen de esa recta PQ tendrá que pasar forzosamente por ese punto doble y por P'. Sobre la imagen de PQ tendrá que estar Q'. También tendrá que estar Q' sobre la recta que une el centro de homología O y Q. Interseccionando PQ' y OQ lograremos la imagen Q' buscada. Para hallar la imagen I' de un punto I en el infinito (punto virtual o impropio), se procede de manera semejante. Se traza la recta PI (que será una dirección), que corta al eje de homología (e) en un punto doble Q. Dicha recta se transforma en la recta P'Q. La imagen del punto I, como cualquier otro punto, se halla sobre la intersección de la recta P'Q con la recta OI (en el plano euclídeo, las rectas PI y IOI' son paralelas). Se verifica que la recta L, paralela al eje de homología e por el punto I', el lugar geométrico de todas las imágenes de los puntos impropios del plano, y recibe la denominación de recta límite. - HomologíaConceptos de ProyectividadAl conjunto de rectas o rayos del espacio que pasan por un punto C se denomina radiación desde C o haz de rectas. A C se le llama centro de proyección.Proyectar un punto sobre un plano es trazar una recta que, con origen en el centro de proyección y pasando por el punto, llegue hasta el plano. Proyectar una figura supone proyectar cada uno de sus vértices y aristas.Si el centro de proyección es propio, la proyección se denomina central o cónica.Si el centro de proyección es impropio (está en el infinito), los rayos son paralelos, y la proyección se denomina cilíndrica o paralela.Un caso particular de la proyección cilíndrica es la ortogonal, en la cual los rayos son perpendiculares al plano de proyección (si la proyección no es ortogonal, es oblicua).Simetría Central EspacialLos planos α y β no se cortan (el eje es impropio)El centro de la homología es real, y se encuentra a igual distancia de ambos planos (es el centro de la simetría)Las rectas límites son impropiasHomología espacialSi suponemos una proyección cónica y una serie de rayos (radiación o haz) que parten desde un centro de proyección, al cortar estos rayos por un plano se obtienen los vértices de una figura plana. Si cortamos el haz por un por un segundo plano, obtenemos una segunda figura plana. Ambas figuras guardan relación de Homología.La Homología es una relación geométrica espacial que relaciona figuras planas situados en diferentes planos mediante las siguientes propiedades:Los puntos homólogos están alineados con un fijo llamado centro de la homología (el centro de proyección).Las rectas homólogas se cortan en un punto de una recta fija llamada eje de la homología. Esta recta es la intersección de los dos planos que contienen a las figuras homólogas.Elementos de la HomologíaEn esta figura se observan los elementos de la homología espacial: planos de las dos figuras homólogas, centro y eje de la homología. Si miramos la figura de perfil (a la derecha), de forma que los planos de las figuras y el eje queden perpendiculares al papel, vemos además dos rectas L y K, también perpendiculares al papel, cuyo significado se explica a continuación.C es el centro de la Homología.Como ya se ha mencionado, el eje (que en la figura de la derecha aparece como un punto) es la recta intersección de los dos planos α y β, en los que están las dos figuras homólogas.El plano paralelo al β que pasa por C corta al plano α en la recta L. Podemos comprobar que los puntos homólogos de esta recta están en el infinito (al unirlos con C mediante una recta, ésta nunca corta al plano α). A esta recta L se le denomina primera recta límite.El plano paralelo al α que pasa por C corta al β en la recta K. Igualmente, los puntos homólogos de esta recta también son impropios (al unirlos con C con una recta, ésta nunca corta al plano β ). A la recta K se le denomina segunda recta límite.O sea, L (primera recta límite) es la recta del plano α cuyos homólogos están en el infinito (son impropios), y K (segunda recta límite) es la recta del plano β cuyos homólogos están en el infinito (son impropios). A estas rectas límites también se les identifica como RL y RL’.La característica o constante de la Homología es un parámetro de la misma, y es igual a la razón doble de la cuaterna formada por dos puntos homólogos A-A’, el centro de la homología C y el punto de corte de la recta A-A’ con el eje.Casos particulares de la HomologíaUna homología en el espacio puede presentar los siguientes casos:Caso general (ver figura anterior)Los planos α y β se cortan (el eje es real)El centro de la homología es propioLas rectas límites son propiasAfinidad espacialLos planos α y β se cortan (el eje es real)El centro de la homología es impropio (dirección de la afinidad)Las rectas límites son impropiasHomotecia EspacialLos planos α y β no se cortan (el eje es impropio)El centro de la homología es real (centro de la homotecia)Las rectas límites son impropiasTraslación espacialLos planos α y β no se cortan (el eje es impropio)El centro de la homología es impropio (dirección de traslación)Las rectas límites son impropiasSimetría Central EspacialLos planos α y β no se cortan (el eje es impropio)El centro de la homología es real, y se encuentra a igual distancia de ambos planos (es el centro de la simetría)Las rectas límites son impropiasTeorema de las Tres homologíasSi dos figuras F’ y F’’ son homólogas de una figura original F en homologías del mismo eje y distintos centros O1 y O2, dichas figuras son homólogas entre sí, mediante otra homología del mismo eje y con centro O3, alineado con O1 y O2.Paso de Homología Espacial a Homología PlanaDos figuras homólogas en el espacio, situadas en dos planos α y β, pueden pasar a ser figuras homólogas en un mismo plano por distintos procedimientos. Este paso de figuras homólogas en el espacio a figuras homólogas en el plano tiene una muy importante aplicación en los sistemas de representación que van a estudiarse en los bloques de geometría descriptiva.Para comprender este paso, recordemos los elementos del esquema de la homología espacial vista de perfil:El plano α contiene a la figura original F1El plano β contiene a la figura homóloga F2El eje de la homología es ELas rectas límites son RL y RL’En la figura de la página siguiente, hemos definido y añadido un tercer plano, el del papel, y una dirección de proyección sobre él. Según esa dirección, obtenemos sobre el papel (plano) las proyecciones de los diferentes elementos de la homología: Figuras F1′ y F2′, rectas límites RLx y RL’x, eje E’ y centro de homología O’.Si colocamos el plano del papel en su posición normal (abatiéndolo), vemos que los elementos proyectados siguen cumpliendo las propiedades de la homología: Los vértices de las figuras F1 y F2 están alineados con el centro de la homología O, y sus aristas se cortan en un punto del eje.Para ilustrar la propiedad de la recta límite, hemos tomado sobre ella un punto M. Por definición, M’ debe estar sobre la recta MC, que hemos trazado. Para encontrarlo, hemos dibujado el segmento que va desde M hasta un vértice de la figura F1, prolongando esta línea hasta el eje. Desde donde toca al eje, hemos lanzado una recta al vértice homólogo en la figura F2, recta cuya prolongación debería tocar a MC en M’. Pero como son paralelas, lo hará en el infinito. O sea, M’ es impropio.Definición de Homología PlanaVisto lo anterior, definimos la Homología plana como la transformación geométrica plana biunívoca que relaciona figuras homólogas en un mismo plano mediante las siguientes propiedades:Los puntos homólogos están alineados con un punto fijo llamado centro de la homologíaLas rectas homólogas se cortan en un punto de una recta fija llamada eje de la homologíaLas definiciones de rectas límites y de característica de la homología son las mismas que en la homología espacial:Las rectas límites son los lugares geométricos de los puntos cuyos homólogos son impropios.La característica de la homología es la razón doble entre el vértice, dos puntos homólogos y el corte de la recta que une a los tres con el eje:Los elementos identificativos de la homología plana son los mismos que los de la homología espacial: El centro de la homología:El eje de la homologíaLas rectas límitesLa constante o característica K es

 la proyección que lleva cada z en su clase de equivalencia. Dotamos a CPn de la
la proyección que lleva cada z en su clase de equivalencia. Dotamos a CPn de la  es abierto si y sólo si
es abierto si y sólo si  lo es. Esta topología convierte a la proyección en una aplicación continua.
lo es. Esta topología convierte a la proyección en una aplicación continua. dada por
dada por ,
, definidas por:
definidas por:![{\displaystyle U_{i}=\{[z]:z\in \mathbb {C} ^{n+1}-\{0\},z_{i}\neq 0\}\qquad \Phi _{i}([z])=({\frac {z_{0}}{z_{i}}},\cdots ,{\hat {\frac {z_{i}}{z_{i}}}},\cdots ,{\frac {z_{n}}{z_{i}}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c85100448ae897abafecd972ea604022c42f14b)
 , se comprueba que el cambio de cartas
, se comprueba que el cambio de cartas  es
es 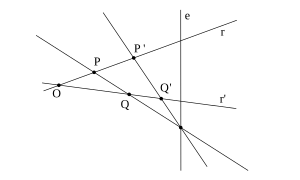
No hay comentarios:
Publicar un comentario