Geometría descriptiva

Geometría proyectiva

La proyección gnomónica (denominada también como proyección central¹ ) es una proyección geográfica caracterizada por tener simetría radial alrededor del punto central (perspectiva centrográfica). Es decir, mediante esta proyección, cualquier punto de una esfera es conectada desde su centro por una línea hasta que interseca en un plano tangente a la esfera (denominado plano de proyección).

Usos

La proyección gnomónica posee varias utilidades en el terreno de la cartografía (mediante el trazado de las cartas gnomónicas) y en gnomónica en el trazado y diseño de algunos relojes solares.

Cartografía

Véase también: Cartografía

En las cartas gnomónicas elaboradas mediante esta proyección toda línea recta es un círculo máximo terrestre y el camino más corto entre dos puntos de la Tierra. Se usa en la navegación aeronáutica para trazar los rumbos verdaderos. Con este sistema no se puede representar un hemisferio completo.

En la proyección polar todos los meridianos son líneas rectas y se disponen radialmente, en la proyección ecuatorial son líneas rectas el ecuador y los meridianos, que se disponen verticalmente, en la proyección oblicua son líneas rectas el ecuador y los meridianos.

Gnomónica

Véase también: Gnomónica

Es empleada esta proyección en el trazado y diseño de las escalas temporales de algunos relojes de sol, así como meridianas solares.

Los círculos mayores se proyectan como líneas rectas en la proyección gnomónica,

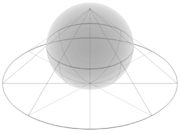
Esquema ilustrativo de una proyección azimutal gnomónica.

proyectividad es una aplicación inducida entre espacios proyectivos mediante una aplicación lineal. Esto es, si ${\displaystyle f:E\rightarrow E'}$ es una aplicación lineal, la proyectividad que induce es de la forma ${\displaystyle f^{*}:P(E)-P(Ker(f))\rightarrow P(E')}$.

Una proyectividad admite unas ecuaciones, que se expresan sencillamente de manera matricial. Para ello basta elegir dos referencias proyectivas ${\displaystyle \{U_{0},U_{1},...,U_{n};U\}}$ y ${\displaystyle \{V_{0},V_{1},...,V_{n};V\}}$ de ${\displaystyle P(E)}$ y ${\displaystyle P(E')}$, que vendrán referidas por las bases ${\displaystyle \{u_{0},u_{1},...,u_{n}\}}$ y ${\displaystyle \{v_{0},v_{1},...,v_{n}\}}$ de ${\displaystyle E}$ y ${\displaystyle E'}$ respectivamente. Así, la ecuación matricial viene dada por ${\displaystyle \rho Y=AX}$, donde ${\displaystyle X,Y}$ son las coordenadas de un punto de ${\displaystyle P(E)}$ y ${\displaystyle P(E')}$ respectivamente, y ${\displaystyle A}$ es la matriz de coeficientes de la aplicación. ${\displaystyle \rho }$ es un escalar de proporcionalidad dado por las coordenadas homogéneas.

El punto del infinito, punto en el infinito o punto impropio es una entidad topológica y geométrica que se introduce a modo de cierre o frontera infinita del conjunto de los números reales. Cuando se añade a la recta real genera una curva cerrada (véase fig.1) conocida como recta proyectiva real, ${\displaystyle \mathbb {R} P^{1}}$, que no es equivalente a la recta real ampliada, que tiene dos puntos distintos en el infinito.

${\displaystyle {\hat {\mathbb {R} }}=\mathbb {R} \cup \{\infty \}}$

fig.1: La "recta proyectiva real (ℝP¹)" con el punto del infinito , genera una curva cerrada.

Topología T

Para que el punto en el infinito represente efectivamente el infinito real se define en ${\displaystyle {\hat {\mathbb {R} }}}$ la topología ${\displaystyle {\hat {T}}}$ formada por todos los conjuntos:

• A, que son abiertos de ${\displaystyle \mathbb {R} }$
• B, que son complementarios de conjuntos compactos (cerrados y acotados) de ${\displaystyle \mathbb {R} }$ .

Los conjuntos A son los abiertos de ${\displaystyle {\hat {\mathbb {R} }}}$ que no contienen el :${\displaystyle \infty }$ mientras que los conjuntos B son los que sí lo contienen.

Sea ${\displaystyle x_{n}\in \mathbb {R} }$ una sucesión de números reales tales que ${\displaystyle \lim _{n\to \infty }x_{n}=\infty }$. Dentro del conjunto de los números reales, esto quiere decir únicamente que:

${\displaystyle \forall K>0\ \exists m\in \mathbb {N} |{\text{ si }}n>m\Rightarrow x_{n}\notin [-K,K]}$

Pero esta misma condición implica en ${\displaystyle {\hat {\mathbb {R} }}}$ que

${\displaystyle \forall B|\infty \in B\ \exists m\in N|{\text{ si }}n>m\Rightarrow x_{n}\in B}$

Es decir, que en ${\displaystyle {\hat {\mathbb {R} }}}$ se escribe también ${\displaystyle \lim _{n\to \infty }x_{n}=\infty }$. Sin embargo, sólo en ${\displaystyle {\hat {\mathbb {R} }}}$ se puede decir que la sucesión ${\displaystyle x_{n}\,}$ converge, puesto que ${\displaystyle \infty \notin \mathbb {R} }$.

En el plano complejo

	fig.cp1: Proyección estereográfica del plano complejo extendido sobre la "esfera de Riemann".
	fig.cp2: La "esfera de Riemann" puede ser visualizada como el plano complejo envuelto alrededor de una esfera.

El punto del infinito también puede añadirse al plano complejo, ${\displaystyle \mathbb {C} ^{1}}$, de manera que se transforme en una superficie cerrada (véase fig.cp1 y fig.cp2), la recta proyectiva compleja, ${\displaystyle \mathbb {C} P^{1}}$, también llamada esfera de Riemann, una esfera sobre el plano complejo y desde cuyo polo superior se proyectan el resto de puntos de la esfera sobre el plano complejo. De este modo, se establece una biyectividad en la que a cada punto de la esfera le corresponde uno del plano complejo. El homólogo del punto desde el que proyectamos estereográficamente se convierte en el punto del infinito.

Rectas paralelas en ℝ²

Al igual que dos rectas secantes comparten un punto, dos rectas paralelas comparten una dirección, por lo que a esas direcciones también se las conoce como puntos impropios de esas rectas en las que se encuentran. Por ejemplo, en ${\displaystyle \mathbb {R} ^{2}}$ no es posible determinar con exactitud la posición del punto del infinito mediante unas coordenadas absolutas ${\displaystyle (x,y)\,}$. Para conseguirlo, se acude a las coordenadas homogéneas ${\displaystyle (x',y',w)\,}$, donde ${\displaystyle x'\,}$ e ${\displaystyle y'\,}$ representan la dirección del vector director de la recta. Las anteriores coordenadas absolutas ${\displaystyle (x,y)\,}$ vienen dadas por:

${\displaystyle (x,y)=\left({x' \over w},{y' \over w}\right)}$

El punto ${\displaystyle (4,6)\,}$ podría representarse, por ejemplo, como ${\displaystyle (8,12,2)\,}$ o como ${\displaystyle (2,3,{\tfrac {1}{2}})}$. La representación del punto del infinito se obtiene igualando ${\displaystyle w=0\,}$, así:

${\displaystyle (x',y',0)\,}$

El punto del infinito del eje OX sería el , el , etc.

Recta polar

En geometría, la recta polar de un punto A respecto a una circunferencia I es el lugar geométrico de los puntos conjugados de A respecto de la circunferencia I.

Este lugar geométrico resulta ser una recta perpendicular a la recta que une el centro de la circunferencia I con el punto A.

En efecto, sea O el centro de la circunferencia I (véase la figura). Sean A y C puntos conjugados respecto de I y s la circunferencia (ortogonal a I) de diámetro AC. Consideremos la recta OA y sea P la otra intersección de la recta OA con la circunferencia s. Observamos que por estar P sobre la circunferencia s y por ser AC diámetro de dicha circunferencia, el triángulo APC es recto en P. Así, el punto C, conjugado de A respecto de I se halla sobre la perpendicular a la recta OA por el punto P. Como esto vale para todo punto conjugado de A concluimos que dicha recta está contenida en el conjunto de puntos conjugados de A respecto de I.

El recíproco también es cierto: Si C es un punto sobre la perpendicular a la recta OA por el punto P entonces dicho punto es conjugado de A respecto de la circunferencia I.

Esto concluye lo que se quería demostrar.

La recta q polar al punto Q respecto de una circunferencia de radio r y centro en O. El punto P es el punto de inversión de Q; la recta polar es la perpendicular desde P a la recta que pasa por O, P y Q.

Inverso Simétrico

Para hallar la recta polar del punto A respecto de la circunferencia I, observemos que la circunferencia s es invariante en la inversión respecto de la circunferencia I. El punto P es por tanto el inverso simétrico de A en esta transformación.

Se dice que el punto A es polo de la recta PC.4

Caso Especial de Circunferencias

El polo de una recta L en una circunferencias C es un punto P que es el inversión en C del punto Q en L que es el más cercano al centro de la circunferencia. Recíprocamente, la recta polar (o polar) de un punto P en una circunferencia C es la recta L tal que su punto más cercano Q a la circunferencia es la inversión de P en C.

Si un punto A yace en la recta polar q de otro punto Q, entonces Q yace en la recta polar a de A. Generalizando, las polares de todos los puntos de la recta q deben pasar a través de su polo, Q.

Aplicaciones

Las polares, definidas por Joseph Diaz Gergonne, juegan un rol crucial en una de las soluciones del Problema de Apolonio.

En dinámica plana un polo es un centro de rotación, la polar es la línea de acción de fuerza y la cónica es la matriz de masa inercial.¹ La relación polo-polar se emplea para definir el centro de oscilación de un cuerpo rígido plano.