Bullrun es un supuesto programa secreto de la NSA cuyo objetivo es burlar la seguridad de distintas tecnologías de cifrado usadas en redes de comunicaciones. Su homólogo británico sería el programa Edgehill de la GCHQ. Ambos programas colaborarían en ciertos campos para la consecución de sus objetivos.
Origen de la información de su existencia
La supuesta existencia de este programa fue revelado por las filtraciones de Edward Snowden. La NSA no ha emitido ninguna respuesta en relación con su presunta existencia. Los informes de The Guardian, The New York Times y Propublica afirman que oficiales de inteligencia pidieron que no se publicara la información por motivos de seguridad nacional
Base legal
La base legal que ampararía la existencia programa sería el artículo 702 de la Ley de Vigilancia de la Inteligencia Extranjera. En él se establece que se puede requerir a un proveedor de servicios "que proporcione al Gobierno inmediatamente toda la información, medios o asistencia necesaria para completar la recopilación" de información de inteligencia extranjera. Se han hecho preguntas sobre si esta ley obliga a divulgar claves criptográficas pero no se ha recibido aclaración1
Actuaciones
Para la consecución de los objetivos del programa se han implementado distintas actuaciones:2
- Influyendo para que se promuevan y adopten estándares, protocolos o sistemas con debilidades. Por ejemplo en los documentos se menciona específicamente a la utilización que la NSA hizo del NIST para insertar una puerta trasera en un estándar de 2006 para la generación de números aleatorios (Dual_EC_DRBG). Posteriormente el estándar fue adoptado como estándar por la Organización Internacional de Estandarización (ISO).3 4
- Trabajando con proveedores de software o hardware criptográfico para que liberen sistemas con debilidades. Por ejemplo implementando directamente puertas traseras o utilizando algoritmos criptográficos con debilidades. Por ejemplo se dice que se pagó a la empresa RSA, filial de EMC, para que usara la fórmula matemática Dual_EC_DRBG como método generador de números aleatorios por defecto de su software de cifrado BSafe aún a sabiendas de la existencia de debilidades.5 4 Según Edward Snowden hay muchos acuerdosmás de este tipo.
- Buscando, y frecuentemente encontrando, debilidades a la seguridad en distintos sistemas de comunicaciones. Por ejemplo se afirma que consiguen descifrar conexiones SSL o tener acceso a muchas de las comunicaciones peer-to-peer de voz y de texto
- Estableciendo una red de infiltrados en la industria de las telecomunicaciones que estén dispuestos a proporcionarles información.
- Identificando y rompiendo claves que resguardan la seguridad de sistemas
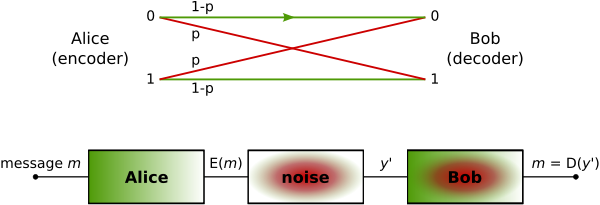
Un Canal Binario Simétrico (en inglés Binary Symmetric Channel, BSC en adelante) es un canal típico de comunicaciones usado habitualmente en la teoría de códigos y teoría de la información. En este modelo, el transmisor envía un bit (que puede tomar valor cero o uno), y el receptor lo recibe. Este bit se recibirá correctamente en la mayoría de los casos, pero existe una probabilidad (probabilidad de error) de que se transmita incorrectamente. La importancia de este canal reside en ser uno de los más simples de analizar, es por ello por lo que es utilizado frecuentemente en la teoría de la información.
Descripción
El BSC es un canal binario que puede transmitir uno de dos símbolos posibles (denominados 0 y 1). La transmisión no es perfecta, y ocasionalmente el receptor recibe el bit equivocado. Nótese que un canal no binario sería capaz de transmistir más de dos símbolos, habiendo múltiples posibilidades.
Este canal se suele usar con bastante frecuencia por ser uno de los más simples para analizar. Es por ello por lo que muchos problemas de la teoría de la comunicaciónse simplifican mediante un modelo BSC. Un BSC puede ser una solución aproximada aceptable para un canal de mayor complejidad.
Definición
Un canal binario simétrico con probabilidad p de fallo es un canal con una entrada binaria y una salida (también binaria), definida con una probabilidad de error p. Esto viene a significar, que si una variable aleatoria X se transmite, y se recibe la variable aleatoria Y, entonces el canal viene determinado por las siguientesprobabilidad condicionada
- Pr( Y = 0 | X = 0) = 1-p
- Pr( Y = 0 | X = 1) = p
- Pr( Y = 1 | X = 0 ) = p
- Pr( Y = 1 | X = 1 ) = 1-p
Donde 0 ≤ p ≤ 1/2. Si p>1/2 entonces el receptor obtendría los bits contrarios (interpretar un 1 cuando se recibe un 0, y viceversa), obteniéndose un canal equivalente con probabilidad de fallo 1-p ≤ 1/2.
Capacidad de un BSC
La capacidad de canal es 1- H(p), donde H(p) es la función de entropía.
El canal binario (BC) es un canal con una entrada y salida binaria. Asociado con cada salida está la probabilidad p que la salida es correcta, y la probabilidad de 1 − p que no lo está. Para cada canal, la capacidad del canal llega a ser:
| |
Aquí, p es la probabilidad de error de bit. Si p = 0 entonces C = 1. Si p = 0.5, C=0. Entonces, si hay una probabilidad igual de recibir un 1 o un 0, independiente de lo que se envió, el canal es completamente irrealizable y no se puede enviar mensajes a través de él. Tal como está definido, la capacidad del canal es un número adimensional. Normalmente se denota la capacidad como una velocidad o tasa, en bits por segundo (bps). Para hacer esto nombramos cada salida a cambiar en la señal. Para un canal de ancho de banda B, podemos transmitir al menos en 2B cambios por segundo. Entonces, la capacidad en bps es 2BC. Para el canal binario tenemos:
| |
Para el canal binario la máxima tasa de bits Rb es 2B. Se nota que C < Rb, en efecto, la capacidad es siempre menor que la tasa de bit. La tasa de datos R, o tasa de información describe la tasa de transferencia de bits de datos a través del canal. En teoría, tenemos:
| |
| |
El teorema de codificación de canal de Shannon se aplica al canal, mas no a la fuente. Si la fuente está codificada óptimamente, podemos replantear el teorema de codificación: Una fuente de información con entropía H {X} puede ser transmitida sin errores sobre un canal siempre y cuando: H {X} ≤ C. La capacidad del canal binario es mucho menor que la calculada de la Ley de Hartley-Shannon (ver). Esto es debido a que la ecuación se aplica a sistemas cuyas salidas puede tomar ciertos valores. Se usan sistemas que obedezcan la ecuación (ver) pues son técnicamente convenientes, y no por que sean deseables.
|
Cenit Polar es un tipo de criptografía scout y es una manera simple de escribir cifrado.
Funcionamiento
La clave Cenit Polar se utiliza al cambiar las letras de la palabra "cenit" por las letras de la palabra "polar" en cada respectiva posición.
| C | E | N | I | T |
| P | O | L | A | R |
Las letras que no aparezcan en ninguna de las dos palabras se mantendrán de esa manera. Por ejemplo, la palabra "lis" (flor) sería, en Cenit Polar, "nas".
Otra manera de verlo es la siguiente:
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | Ñ | O | P | Q | R | S | T | U | V | W | X | Y | Z |
| I | B | P | D | O | F | G | H | A | J | K | N | M | L | Ñ | P | C | Q | T | S | R | U | V | W | X | Y | Z |
Otras Técnicas de Scout
- Clave +3 o Cifrado César desplazado en 3
La Clave +3 es una forma simple de escribir cifrado. Consiste en sumar 3 letras a cada letra del mensaje. La palabra AMISTAD quedará así DOLVWDG.
Otra manera de verlo es la siguiente:
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | Ñ | O | P | Q | R | S | T | U | V | W | X | Y | Z |
| D | E | F | G | H | I | J | K | L | M | N | Ñ | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C |
- Claves Agujerito y Murciélago
Estas claves tienen la diferencia de que cada letra que conforma la clave es reemplazada por un número y las demás letras no se modifican.
| A | G | U | J | E | R | I | T | O |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
La palabra AMISTAD quedaría escrita como: 1m7s81d, pues las letras se repiten al no estar contenidas en la palabra "agujerito".
| M | U | R | C | I | E | L | A | G | O |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
La palabra AMISTAD quedaría escrita como: 704st7d , pues las letras se repiten al no estar contenidas en la palabra "MURCIÉLAGO".
Otra manera de verlo es la siguiente:
Agujerito
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | Ñ | O | P | Q | R | S | T | U | V | W | X | Y | Z |
| 1 | B | C | D | 5 | F | 2 | H | 7 | 4 | K | L | M | N | Ñ | 9 | P | Q | 6 | S | 8 | 3 | V | W | X | Y | Z |
Murciélago
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | Ñ | O | P | Q | R | S | T | U | V | W | X | Y | Z |
| 7 | B | 3 | D | 5 | F | 8 | H | 4 | J | K | 6 | 0 | N | Ñ | 9 | P | Q | 2 | S | T | 1 | V | W | X | Y | Z |
Esta clave lleva su nombre por uno de sus creadores, Samuel Morse. Él y sus colaboradores idearon un sistema de reemplazo de las letras y números dígitos por una combinación de rayas y puntos. Con ellas reemplazaban las letras, permitiendo transmitir un mensaje por medios electrónicos, auditivos o luminosos. En el caso scout también es posible usar papel.
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | Ñ | O | P | Q | R | S | T | U | V | W | X | Y | Z |
| · − | − · · · | − · − · | − · · | · | · · − · | − − · | · · · · | · · | · − − − | − · − | · − · · | − − | − · | − − · − − | − − − | · − − · | − − · − | · − · | · · · | − | · · − | · · · − | · − − | − · · − | − · − − | − − · · |
Por ejemplo, SOS es · · · / − − − / · · ·
Tabla de decodificación
| · | − | · · | · − | − · | − − | · · · | · · − | · − · | · − − | − · · | − · − | − − · | − − − | · · · · | · · · − | · · − · | · − · · | · − − · | · − − − | − · · · | − · · − | − · − · | − · − − | − − · · | − − · − | − − · − − |
| E | T | I | A | N | M | S | U | R | W | D | K | G | O | H | V | F | L | P | J | B | X | C | Y | Z | Q | Ñ |
El Chaocipher1 es una máquina de cifrado inventada por John F. Byrne en 1918 la cual está descrita en su libro autobiográfico Silent Years2 (Años silenciosos). Byrne creía que el sistema implementado en el chaocipher era simple e inquebrable. Byrne sostenía que la máquina que él usaba para encriptar sus mensajes cabría dentro de una caja de cigarros. Byrne ofreció una recompensa a cualquiera que lograra descifrar su sistema.
En mayo de 2010 la familia Byrne donó todos los documentos y artefactos3 relacionados con el Chaocipher al Museo Nacional de Criptología en Ft. Meade, Maryland,Estados Unidos. Esto llevó a que se descubriera el algoritmo del sistema Chaocipher.
Descripción del sistema Chaocipher
El sistema Chaocipher consiste en dos alfabetos, con un alfabeto «derecho» usado para localizar el texto escrito mientras que el otro alfabeto, «izquierdo», es usado para la lectura de las letras del correspondiente texto cifrado. El algoritmo subyacente está relacionado con el concepto de la sustitución dinámica,5 mediante el cual los dos alfabetos son ligeramente modificados después de que cada letra de texto que va ingresando es cifrada. Esto lleva a la generación de unos alfabetos no lineales y altamente difusos a medida que el cifrado va progresando.
El decifrado es idéntico al encifrado, con las letras del texto cifrado siendo localizadas en el alfabeto izquierdo mientras que las letras del texto correspondiente son leídas desde el alfabeto derecho.
Una descripción detallada del algoritmo que utiliza el Chaocipher está disponible,4 así también como debates sobre el cifrado de texto6 y la solución al desafío de Byrne.7
Puntos de interés
Henry E. Langen,8 editor de la revista "The Cryptogram" (El Criptograma) durante la época en la que apareció este sistema, dijo en una declaración:
- "El (Byrne) explicó que la máquina está construida de modo parecido al mecanismo de las máquinas de escribir con dos discos giratorios y con los alfabetos dispuestos a lo largo de la periferia en un completo desorden...con solo dos discos utilizados, estoy un poco confundido en cuanto a cómo esto puede dar lugar a que se genere un completo caos en los mensajes de texto".
No hay comentarios:
Publicar un comentario