Cifrados clásicos
Acme Commodity and Phrase Code fue un libro de códigos publicado en 1923 por la Acme Code Company (A. C. Meisenbach, Acme Commodity and Phrase Code, Acme Code Co., San Francisco, CA, 1923.) el cual contenía 100.000 códigos estandarizados que se asignaban a frases de uso común (algunas muy largas). De esta forma se permitía escribir los telegramas de forma más corta y así ahorrar dinero.
2 3 Los códigos eran de 5 letras formando así una especie de 'palabra'. Por este motivo a los códigos se les solía llamar codeword. La probabilidad de que una modificación aleatoria de dichos códigos diera lugar a otro código es de 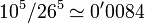 (el alfabeto del idioma inglés tiene 26 letras). Los códigos estaban definidos de tal forma que permitían cierto grado de detección y corrección de errores, considerándose este código como precursos de ese tipo de prácticas. Todos los códigos se diferenciaban en al menos dos letras. Además ninguna transposión de dos letras adyacentes daban lugar a otro código válido. Observar que con estas características si hay un error en la trásmisión y una letra es cambiada por otra, entonces por un lado podemos detectar el error y por otro podemos proponer 5 candidatos como posibles orígenes de ese código erróneo. Entre esos código podríamos elegir el más apropiado al contexto del mensaje. Además la forma en que se definen los códigos protege también frente a posible transposiciones de letras.
(el alfabeto del idioma inglés tiene 26 letras). Los códigos estaban definidos de tal forma que permitían cierto grado de detección y corrección de errores, considerándose este código como precursos de ese tipo de prácticas. Todos los códigos se diferenciaban en al menos dos letras. Además ninguna transposión de dos letras adyacentes daban lugar a otro código válido. Observar que con estas características si hay un error en la trásmisión y una letra es cambiada por otra, entonces por un lado podemos detectar el error y por otro podemos proponer 5 candidatos como posibles orígenes de ese código erróneo. Entre esos código podríamos elegir el más apropiado al contexto del mensaje. Además la forma en que se definen los códigos protege también frente a posible transposiciones de letras.
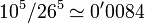 (el alfabeto del idioma inglés tiene 26 letras). Los códigos estaban definidos de tal forma que permitían cierto grado de detección y corrección de errores, considerándose este código como precursos de ese tipo de prácticas. Todos los códigos se diferenciaban en al menos dos letras. Además ninguna transposión de dos letras adyacentes daban lugar a otro código válido. Observar que con estas características si hay un error en la trásmisión y una letra es cambiada por otra, entonces por un lado podemos detectar el error y por otro podemos proponer 5 candidatos como posibles orígenes de ese código erróneo. Entre esos código podríamos elegir el más apropiado al contexto del mensaje. Además la forma en que se definen los códigos protege también frente a posible transposiciones de letras.
(el alfabeto del idioma inglés tiene 26 letras). Los códigos estaban definidos de tal forma que permitían cierto grado de detección y corrección de errores, considerándose este código como precursos de ese tipo de prácticas. Todos los códigos se diferenciaban en al menos dos letras. Además ninguna transposión de dos letras adyacentes daban lugar a otro código válido. Observar que con estas características si hay un error en la trásmisión y una letra es cambiada por otra, entonces por un lado podemos detectar el error y por otro podemos proponer 5 candidatos como posibles orígenes de ese código erróneo. Entre esos código podríamos elegir el más apropiado al contexto del mensaje. Además la forma en que se definen los códigos protege también frente a posible transposiciones de letras.
El libro fue extremadamente popular en el mundo de los negocios a principios del siglo XX.
Atbash es un método muy común de cifrado (criptografía) del alfabeto hebreo. Pertenece a la llamada criptografía clásica y es un tipo decifrado por sustitución. Se le denomina también método de espejo, pues consiste en sustituir la primera letra (álef) por la última (tav), la segunda (bet) por la penúltima (shin) y así sucesivamente. Uno de sus usos más célebres se da en el libro de Jeremías,1 donde a fin de no nombrar Babilonia (בבל, Babel) se utiliza el término, en atbash, Sesac (ששך, Sheshakh).
La tabla de sustitución de atbash para el alfabeto hebreo es la siguiente:
| Original | א | ב | ג | ד | ה | ו | ז | ח | ט | י | כ | ל | מ | נ | ס | ע | פ | צ | ק | ר | ש | ת |
| Clave | ת | ש | ר | ק | צ | פ | ע | ס | נ | מ | ל | כ | י | ט | ח | ז | ו | ה | ד | ג | ב | א |
Una tabla de atbash para el alfabeto español sería así:
| Original | a | b | c | d | e | f | g | h | i | j | k | l | m | n | ñ | o | p | q | r | s | t | u | v | w | x | y | z |
| Clave | Z | Y | X | W | V | U | T | S | R | Q | P | O | Ñ | N | M | L | K | J | I | H | G | F | E | D | C | B | A |
En todo caso, hay que tener presente que este método de cifrado se ideó para un abyad en el que solo se escriben las consonantes, que luego se vocalizan de manera más o menos arbitraria y, así, prácticamente cualquier palabra hebrea es pronunciable al cifrarse en atbash. En idiomas con escritura alfabética, como el español, es infrecuente que una palabra codificada en atbash sea pronunciable.
El proceso de (de)codificacion se realiza mediante la sustitucion de la posicion que ocupa en el abecedario cada uno de los caracteres en el texto original, por el abecedario invertido.
- Tabla de intercambio de caracteres. Los caracteres de arriba se sustituyen por los de abajo para cifrar el texto:
- Tabla de intercambio de caracteres. Los caracteres de arriba se sustituyen por los de abajo para cifrar el texto:
a b c d e f g h i j k l m n o p q r s t u v w x y z
z y x w v u t s r q p o n m l k j i h g f e d c b a
La sustitución es directa, es decir, la a => z, b => y, etc...
El método ATBASH
Es un método de codificación del alfabeto hebreo que consiste en utilizar la letra simétrica a la dada según el siguiente esquema:
A=Z | N=M
B=Y | O=L
C=X | P=K
D=W | Q=J
E=V | R=I
F=U | S=H
G=T | T=G
H=S | U=F
I=R | V=E
J=Q | W=D
K=P | X=C
L=O | Y=B
M=N | Z=A
- Se supone que fue utilizado ya entre el 600 y 500 aC.
- Es utilizado en “El libro de Jeremías” al contar la historia de Babel.
- Es citado en “El código da Vinci”.
La cifra de Delastelle debe su nombre a su inventor, el francés Félix-Marie Delastelle (1840-1902), quien había descrito por primera vez el principio en la Revue du Génie civil en 1895, bajo el nombre de "nueva criptografia".
El algoritmo utiliza una grilla de cifrado / descifrado análoga a la del cuadrado de Polibio. Luego de anotar las coordenadas de varias letras sin cifrar, mezcla las coordenadas y lee después en la grilla las letras cifradas con las coordenadas mezcladas.
Este procedimiento se llama también tomográmico.
El Traité élémentaire de cryptographie de Delastelle, único criptógrafo civil importante de la época, fue publicado por Gauthier-Villars en 1902.
Polibio aparece en los libros de Criptografía como el inventor de un procedimiento para escribir las letras como pares de números. Mediante una tabla se hace corresponder a cada carácter de un alfabeto de 25 letras un par de números. La tabla de Polibio tiene la forma siguiente:
| 1 | 2 | 3 | 4 | 5 | |
| 1 | A | B | C | D | E |
| 2 | F | G | H | I/J | K |
| 3 | L | M | N | O | P |
| 4 | Q | R | S | T | U |
| 5 | V | W | X | Y | Z |
Por ejemplo, la palabra Polibio se escribiría 35 34 31 24 12 24 34.
Puede también utilizarse la tabla de Polibio para convertir en números un alfabeto desordenado previamente por medio de una palabra clave. Por ejemplo, si usamos para cifrar el alfabeto la palabra MUESCA, resultaría:
| 1 | 2 | 3 | 4 | 5 | |
| 1 | M | U | E | S | C |
| 2 | A | B | D | F | G |
| 3 | H | I/J | K | L | N |
| 4 | O | P | Q | R | T |
| 5 | V | W | X | Y | Z |
Polibio no concibió la tabla como un modo de escritura secreta sino como un medio de comunicarse a distancia por medio de antorchas, como una especie de telégrafo primitivo. En las prisiones de la Rusia zarista se utilizaba para comunicarse, mediante golpes en las paredes, una tabla similar a la de Polibio pero de seis números para poder contener el alfabeto cirílico.
La tabla de Polibio tiene tres características muy interesantes desde el punto de vista de la criptografía:
- En primer lugar sirve para transformar los caracteres alfabéticos en números lo que hace posible aplicar posteriormente transformaciones de tipo aritmético.
- En segundo lugar permite reducir el número de caracteres de 25 a 5 lo que puede hacer más sencilla la transmisión del mensaje.
- Finalmente, a cada carácter le hace corresponder dos cifras que pueden ser manipuladas separadamente mediante técnicas de trasposición.
Una de las técnicas de cifrado que utilizan como paso previo la tabla de Polibio es la cifra bífida del criptógrafo francés Félix-Marie Delastelle. Cada par de letras se cifra mediante una tabla de Polibio y se ponen sus coordenadas en columna. Por ejemplo, para cifrar el par tu con la tabla anterior:
| t | u | |
|---|---|---|
| 4 | 1 | O |
| 5 | 2 | W |
Como el par (4,1) se corresponde con la letra O y el par (5,2) con la letra W, las dos letras tu se cifran como OW. El cifrado de Delastelle es autorecíproco, es decir, el procedimiento de cifrado es el mismo que el de descifrado.
Mediante el formulario siguiente se puede cifrar un mensaje por medio de la tabla de Polibio que se quiera. Hay que rellenar el alfabeto de cifrado teniendo cuidado de no incluir la letra J. A los efectos de la Tabla de Polibio, la I y la J son la misma letra. Se puede marcar la casilla correspondiente para obtener el cifrado de Delastelle. El mensaje cifrado por este último procedimiento se puede descifrar con este mismo formulario pues, como hemos dicho, el cifrado de Delastelle es autorecíproco.
El cifrado afín también se le llama cifrado de transformación afín o cifrado monoalfabético genérico. Es un tipo de cifrado por sustitución en el que cada símbolo del alfabeto en claro (el alfabeto del texto en claro) es sustituido por un símbolo del alfabeto cifrado (el alfabeto del texto cifrado) siendo el número de símbolos del alfabeto en claro igual que el número de símbolos del alfabeto cifrado. Para hallar el símbolo del alfabeto cifrado que sustituye a un determinado símbolo del alfabeto en claro, se usa una función matemática afín en aritmética modular. Para poder aplicar la función matemática lo primero que hay que hacer es asignar un orden que a cada símbolo de cada uno de los alfabeto le asocie un número de orden. Una vez establecido esto, la fórmula matemática tiene la siguiente forma:
Donde:
 : Identifica el símbolo i del texto cifrado
: Identifica el símbolo i del texto cifrado- a: Se la llama constante de decimación
 : Identifica el símbolo i del texto en claro
: Identifica el símbolo i del texto en claro- b: Se la llama constante de desplazamiento
- n: Es el número de símbolos del alfabeto de cifrado (el orden)
Los valores numéricos de  y
y  para traducirlos a símbolos de alfabetos, se interpretan como la posición del símbolo en el orden elegido de cada alfabeto.
para traducirlos a símbolos de alfabetos, se interpretan como la posición del símbolo en el orden elegido de cada alfabeto.
 y
y  para traducirlos a símbolos de alfabetos, se interpretan como la posición del símbolo en el orden elegido de cada alfabeto.
para traducirlos a símbolos de alfabetos, se interpretan como la posición del símbolo en el orden elegido de cada alfabeto.
Sobre los valores de las constantes podemos decir:
 ya que para la sustitución definida para cualquier otro valor de a se puede encontrar un b cuya sustitución es equivalente.
ya que para la sustitución definida para cualquier otro valor de a se puede encontrar un b cuya sustitución es equivalente.- Para que se defina una sustitución utilizable es necesario que
 . Además podemos acotar a que
. Además podemos acotar a que  , ya que la sustitución definida con valores de
, ya que la sustitución definida con valores de  negativos se pueden obtener con el mismo valor de
negativos se pueden obtener con el mismo valor de  pero sin el signo.
pero sin el signo. - Por las propiedades de la aritmética modular, para que este tipo de cifrado sea operativo es necesario que
 y
y  sean primos entre sí, también llamados coprimoso primos relativos (
sean primos entre sí, también llamados coprimoso primos relativos (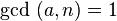 ). Esta condición es necesaria para que
). Esta condición es necesaria para que  tenga inverso de la multiplicación (
tenga inverso de la multiplicación ( ) lo cual es necesario para poder descifrar. Además se puede demostrar1 que sea
) lo cual es necesario para poder descifrar. Además se puede demostrar1 que sea 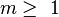 y sea
y sea 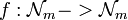 definida con
definida con  con
con  y
y  enteros, f es una biyección sí y sólo sí
enteros, f es una biyección sí y sólo sí  .
.
Por ejemplo, podemos modelizar el cifrado César, suponiendo el orden natural del alfabeto de n símbolos, por la siguiente ecuación:
En este cifrado la clave viene definida por los valores enteros a y b, y por el orden usado en el alfabeto de claro y en el alfabeto en claro, ambos alfabetos son el mismo número de símbolos, m. Por tanto es un cifrado de clave simétrica.
Para descifrar habrá que realizar el proceso inverso que se puede describir con la función matemática 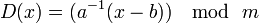 donde
donde  representa alinverso multiplicativo en aritmética modular (el menor número que
representa alinverso multiplicativo en aritmética modular (el menor número que  ).
).
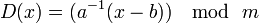 donde
donde  representa alinverso multiplicativo en aritmética modular (el menor número que
representa alinverso multiplicativo en aritmética modular (el menor número que  ).
).
Este tipo de cifrado se ha generalizado para su uso como cifrador de bloque en los llamados cifradores afínes por bloques.
Clasificación
Podemos clasificar los cifradores afines según los valores de a y b:
- Si
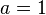 se dice que el cifrado es por desplazamiento puro. Con ello la función matemática queda
se dice que el cifrado es por desplazamiento puro. Con ello la función matemática queda 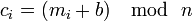 . Por tanto para descifrar tenemos que realizar la operación
. Por tanto para descifrar tenemos que realizar la operación  donde
donde  es el inverso de la adición en el conjunto de los enteros módulo n. Por ejemplo si
es el inverso de la adición en el conjunto de los enteros módulo n. Por ejemplo si 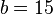 y
y  entonces
entonces  ya que se tiene que cumplir
ya que se tiene que cumplir 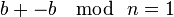 .
.
- Observar que si a=1 y b=0 y el alfabeto en claro y el alfabeto cifrado son iguales y con el mismo orden definido, entonces cada símbolo se sustituirá por sí mismo y por tanto no habrá cifrado.
- Si
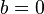 se dice que el cifrado es por decimación pura. Con ello la función matemática queda
se dice que el cifrado es por decimación pura. Con ello la función matemática queda  . Por tanto para descifrar tenemos que realizar la operación
. Por tanto para descifrar tenemos que realizar la operación  donde
donde  es el inverso de la multiplicación en el conjunto de los enteros módulo n.
es el inverso de la multiplicación en el conjunto de los enteros módulo n.
- Si
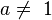 y
y  se dice que el cifrado es por sustitución afín. Por tanto en la función matemática
se dice que el cifrado es por sustitución afín. Por tanto en la función matemática  al despejar para poder descifrar obtenemos
al despejar para poder descifrar obtenemos  , la última igualdad aplicando propiedad elemental de aritmética modular.
, la última igualdad aplicando propiedad elemental de aritmética modular.
Ejemplo
Supongamos que a=5 y b=15 y usamos el alfabeto castellano con m=27 en el orden habitual como alfabeto en claro y como alfabeto cifrado. Usando el cifrado afín definido de esa forma el símbolo 'a' se convertirá en  y, por tanto, el carácter asociado será el que ocupa la posición 20 empezando desde 0, la 's'. Aplicando el mismo algoritmo podemos obtener que el texto cifrado de 'plantanuclear' es 'ntsdlspctmsb'.
y, por tanto, el carácter asociado será el que ocupa la posición 20 empezando desde 0, la 's'. Aplicando el mismo algoritmo podemos obtener que el texto cifrado de 'plantanuclear' es 'ntsdlspctmsb'.
 y, por tanto, el carácter asociado será el que ocupa la posición 20 empezando desde 0, la 's'. Aplicando el mismo algoritmo podemos obtener que el texto cifrado de 'plantanuclear' es 'ntsdlspctmsb'.
y, por tanto, el carácter asociado será el que ocupa la posición 20 empezando desde 0, la 's'. Aplicando el mismo algoritmo podemos obtener que el texto cifrado de 'plantanuclear' es 'ntsdlspctmsb'.
Para descifrar aplicamos la fórmula de descifrado. Para a=5 el inverso multiplicativo es 135 (aprovecho que a=5 y m=27 son primos relativos y las propiedades de losinversos multiplicativos en aritmética modular). Por tanto para s=20 tenemos  . El carácter que ocupa la posición 0 del alfabeto es la 'a'.
. El carácter que ocupa la posición 0 del alfabeto es la 'a'.
 . El carácter que ocupa la posición 0 del alfabeto es la 'a'.
. El carácter que ocupa la posición 0 del alfabeto es la 'a'.Criptoanálisis
El cifrado afín es vulnerable a ataques criptoanalíticos, los más habituales son:2
- El análisis de frecuencias
- La búsqueda en el espacio de claves
Análisis de frecuencias
El cifrado afín, como cualquier otro cifrado por sustitución, es vulnerable a ataques por análisis de frecuencias.
Ejemplo
Por ejemplo supongamos que observando un texto cifrado podemos inferir que usa un alfabeto de cifrado con m=26 símbolos. Si suponemos que el texto en claro que ha sido cifrado está escrito en idioma inglés con un alfabeto de m=26 símbolos. En el inglés los caracteres más frecuentes son la E y después la T. Si suponemos el orden habitual entonces E=4 y T=19. Analizando una cantidad suficiente de mensaje cifrado obtenemos que, por ejemplo, las más frecuentes son la V y después la E. Si suponemos el orden habitual V=21 y E=4. Del resultado anterior podemos ver que probablemente la E esté siendo sustutida por la V y la T por la E. Por tanto podemos obtener las siguientes congruencias:
Si restamos de la primera ecuación la segunda, obtenemos lo siguiente:
resolviendo obtenemos:
Sustituyendo a en la primera ecuación original obtenemos:
despejando
A partir de estos valores puedo hallar el inverso multiplicativo, por ejemplo usando el algoritmo de Euclides extendido, 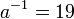 . Ahora toca verificar nuestras suposiciones, si aplicando los valores obtenidos obtenemos un texto inteligible entonces habíamos acertado en nuestras suposiciones, en otro caso habremos fallado y será necesario hacer otras suposiciones.
. Ahora toca verificar nuestras suposiciones, si aplicando los valores obtenidos obtenemos un texto inteligible entonces habíamos acertado en nuestras suposiciones, en otro caso habremos fallado y será necesario hacer otras suposiciones.
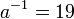 . Ahora toca verificar nuestras suposiciones, si aplicando los valores obtenidos obtenemos un texto inteligible entonces habíamos acertado en nuestras suposiciones, en otro caso habremos fallado y será necesario hacer otras suposiciones.
. Ahora toca verificar nuestras suposiciones, si aplicando los valores obtenidos obtenemos un texto inteligible entonces habíamos acertado en nuestras suposiciones, en otro caso habremos fallado y será necesario hacer otras suposiciones.Búsqueda en el espacio de claves
La función de Euler nos da el número de enteros de  que tienen inverso para la multiplicación. Aplicando dicha fórmula a n=27 el valor de la función de Euler es 27*(1-1/3)=18. De este resultado podemos concluir que el número de posibles cifradores definidos con n=27 es 26(posibles valores de b)*18(posibles valores de a)=486. Este valor es realmente pequeño y un ordenador podría probar todas las posibles combinaciones muy rápidamente.
que tienen inverso para la multiplicación. Aplicando dicha fórmula a n=27 el valor de la función de Euler es 27*(1-1/3)=18. De este resultado podemos concluir que el número de posibles cifradores definidos con n=27 es 26(posibles valores de b)*18(posibles valores de a)=486. Este valor es realmente pequeño y un ordenador podría probar todas las posibles combinaciones muy rápidamente.
 que tienen inverso para la multiplicación. Aplicando dicha fórmula a n=27 el valor de la función de Euler es 27*(1-1/3)=18. De este resultado podemos concluir que el número de posibles cifradores definidos con n=27 es 26(posibles valores de b)*18(posibles valores de a)=486. Este valor es realmente pequeño y un ordenador podría probar todas las posibles combinaciones muy rápidamente.
que tienen inverso para la multiplicación. Aplicando dicha fórmula a n=27 el valor de la función de Euler es 27*(1-1/3)=18. De este resultado podemos concluir que el número de posibles cifradores definidos con n=27 es 26(posibles valores de b)*18(posibles valores de a)=486. Este valor es realmente pequeño y un ordenador podría probar todas las posibles combinaciones muy rápidamente.
Para hacer crecer este valor podemos usar una clave para que nos sirva como un desplazamiento adicional para cada símbolo. En esta situación, el cifrador se convierte en un cifrador de sustitución monoalfabético general en el que cada símbolo del alfabeto en claro es susituido por un símbolo del alfabeto cifrado. En este tipo de cifradores las posibles sustituciones son n!=27! (el número de las posibles permutaciones). Por ejemplo, si la clave es "HOLA" al primer símbolo de texto cifrado obtenido por la función, se le aplicará un desplazamiento de 8 (la H ocupa la octava posición), y así se sigue sucesivamente y cuando se acabe la clave volvemos a empezar.
Algoritmo Afín
Afín. (Sustitución - Monoalfabética – Monográmica).
Este algoritmo data de 1967 y es un método denominado ‘de punto interior’. Existen tres tipos de cifrado por sustitución afin:

Donde:
Ejemplo.
Si tenemos los siguientes valores a=3, b=5 y m=26, y el mensaje que vamos a cifrar es "hola".
Numeraremos en orden alfabético nuestras letras de forma tal que A=0, B=1, ... ,Z=25
| A | B | C | D | E | F | G | H | I | J | K | L | M |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
La funcion de cifrado que utilizaremos será:
e( x ) = 3 x + 5 (mod 26)
h=7 => e( 7 ) = 7 * 3 + 5 = 26 mod 26 = 0 = a
o=14 => e( 14 ) = 14 * 3 + 5 = 47 mod 26 = 21 = v
l=11 => e( 11 ) = 11 * 3 + 5 = 38 mod 26 = 12 = m
a=0 => e( 0 ) = 0 * 3 + 5 = 5 = f
Nuestro mensaje "hola" cifrado es "avmf"
La funcion de descifrado es d ( x ) = a−1 ( x − b )(mod m ) donde a−1 es la inversa multiplicativa de a modulo m; en el caso de a = 3, a−1 = 9 ya que 3 · 9 = 27 = 1 modulo 26, por lo tanto la función de desencriptación será:
d ( x ) = 9 ( x − 5)(mod 26)



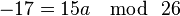



No hay comentarios:
Publicar un comentario