densidad numérica (símbolo: n) es una cantidad intensiva utilizada para describir el grado de concentración de objetos contables (partículas elementales, moléculas, fonones, células, galaxias, etc.) en el espacio físico: densidad numérica volumétrica tridimensional, densidad numérica superficial bidimensional o densidad numérica lineal unidimensional. La densidad de población es un ejemplo de una densidad numérica superficial. El término concentración numérica (símbolo: C) es utilizado a veces en química para la misma cantidad, en particular cuando se compara con otras concentraciones.
Definición
 ,
,
donde
- N es el número total de objetos en un volumen V.
Aquí se está suponiendo2 que N es lo suficientemente grande, de tal forma que al redondear el conteo al entero más próximo no se introduce gran cantidad de error. Sin embargo V se escoge de tal manera que sea lo suficientemente pequeña para que el valor resultante de n no dependa demasiado del tamaño o la forma del volumen V.
Unidades
En el Sistema Internacional de Unidades, la densidad numérica está medida en m−3, aunque también se usa comúnmente cm−3. Sin embargo, estas unidades no son muy prácticas cuando se trabaja con átomos o moléculas de gases, líquidos o sólidos a temperatura ambiente y presión atmosférica, ya que los números resultantes son demasiado grandes (del orden de 1020). Usando la densidad numérica de un gas ideal a 0 °C y 1 atm como base: se introduce 1 amagat = 2.6867774×1025 m−3 (igual a la constante de Loschmidt) como unidad de densidad numérica, para cualquier sustancia en cualquier condición (no necesariamente limitada a un gas ideal a 0 °C y 1 atm).3
Uso
Usando la densidad numérica como función de las coordenadas espaciales, el número total de objetos N en todo el volumen V se puede calcular como
 ,
,
donde dV = dx dy dz es un elemento de volumen. Si cada objeto posee la misma masa m0, la masa total m de todos los objetos en el volumen V puede expresarse como
 .
.
Expresiones similares son válidas para la carga eléctrica o cualquier otra cantidad extensiva asociada con objetos contables. Por ejemplo, al remplazar m → q (carga total) y m0 → q0 (carga de cada objeto) en la ecuación anterior, se obtiene la expresión correcta para la carga.
La densidad numérica de moléculas disueltas en un disolvente se llama a veces concentración. Sin embargo, usualmente la concentración se expresa como el número demoles por unidad de volumen (por lo que se le llama concentración molar).
Relación con otras cantidades
Concentración molar
Para cualquier sustancia, la densidad numérica n (en unidades de m−3) puede expresarse en términos de su concentración molar c (en unidades de mol/m3) como:
 ,
,
donde NA es la constante de Avogadro ≈ 6,022 × 1023 mol−1. Esto es válido incluso si la unidad de dimensión espacial, metro, es remplazada por otra unidad de dimensión espacial de forma consistente tanto en n como en c. Por ejemplo, es válido si n está en unidades de cm³ y c en unidades de mol/cm³, o si n está en unidades de L−1 y c en unidades de mol/L, etc.
Densidad de masa
Para átomos o moléculas con una masa molecular bien definida, M (en unidades de kg/mol), la densidad numérica puede expresarse en términos de la densidad de masaρ (en unidades de kg/m3) como
 .
.
Nótese que el cociente M/NA es la masa de un solo átomo o molécula, en unidades de kg.
Ejemplos
La siguiente tabla lista ejemplos comunes de densidades numéricas a 1 atm y 20 °C, excepto donde se indique lo contrario.
| Material | Number density (n) | Concentración molar (c) | Densidad (ρ) | Masa molar (M) | |
|---|---|---|---|---|---|
| Unidades | (1027 m−3) o (1021 cm−3) | (amagat) | (103 mol/m3) o (mol/L) | (103 kg/m3) o (g/cm3) | (10−3 kg/mol) or (g/mol) |
| gas ideal | 0.02504 | 0.932 | 0.04158 | 41.58 × 10−6×M | M |
| aire seco | 0.02504 | 0.932 | 0.04158 | 1.2041 × 10−3 | 28.9644 |
| agua | 33.3679 | 1241.93 | 55.4086 | 0.99820 | 18.01524 |
| diamante | 176.2 | 6556 | 292.5 | 3.513 | 12.01 |
Densidad
Un número real es un número que existe en la realidad, lo que significa que cada punto en la recta numérica real representa un número real.
Puede ser un número racional o irracional, un número entero o trascendental, de cualquier tipo.
Existe una serie de propiedades de los números reales que deben ser estudiadas a profundidad para entender el concepto de los números reales y también las operaciones basadas en números reales.
La densidad es una propiedad fundamental de los números reales, según la cual los números reales son densos en naturaleza, o en términos simples, entre dos números reales existe un tercer número real, en todos los casos.
En la figura anterior, existen una cantidad infinita de números reales entre cero y uno.
A la luz de la declaración anterior se puede concluir que la recta numérica no tiene espacios entre ella y por esta razón es muy densa, representando así una cantidad infinita de números sobre ella.
Para demostrar la afirmación anterior, mire la prueba debajo. Consideremos dos números reales x e y, donde x es menor que y.
Entonces,  debe estar en algún lugar entre los dos números. Ahora, si r y s son números reales, entonces
debe estar en algún lugar entre los dos números. Ahora, si r y s son números reales, entonces  representa el conjunto de números infinitos que existen entre x e y en la recta numérica real.
representa el conjunto de números infinitos que existen entre x e y en la recta numérica real.
La ecuación anterior también se puede probar,
r*x + s*y/ r + s = (r + s)*x + s*(y – x)/ r + s
= x + (s/ r + s)*(y – x) > x = r*(x – y) + (r + s)*y/ r + s = y - (s/ r + s)*(y – x) < y.
La propiedad de la densidad es dependiente de un conjunto que es mayor que el subconjunto dado y en el cual podemos acomodar el subconjunto dado.
Lo que significa que, si B es un conjunto que contiene todos los elementos del conjunto A, y se asume que A es denso en B, entonces existen una cantidad de elementos infinitos entre ellos como B / A.
Está fuertemente establecido que no puede existir un par de números reales que no contengan otro número real entre ellos.
Esto también significa que la recta numérica real está formada de manera muy íntima teniendo una infinidad de números sobre ella.
Sobre la recta numérica real, existen algunos números racionales entre el conjunto de dos números reales, existen algunos números irracionales entre un conjunto de dos números racionales; existen algunos números racionales entre un conjunto de dos números irracionales.
La recta numérica real es tal que para cualquier número real a y sean mayores que cero, entonces otro número racional es  .
.
Esta propiedad viola la propiedad de numerabilidad que los estudiantes leen desde temprana edad, de que podemos contar los números reales.
Lo verdaderamente cierto, es que los números reales no se pueden contar.
Tomemos ahora un ejemplo para clarificar el concepto. Demostrar que si r – s > 1, entonces para un número entero k lo siguiente es cierto, r
Supongamos que un número entero el cual es el mayor entero que satisface la ecuación <= r.
Entonces para la ecuación r – s > 1, podemos mantener los valores, y> x + 1> = + 1.
Y a nuestro conocimiento <= x < + 1 se mantiene cierto.
Por tanto al comparar las ecuaciones, x < + 1 < y se convierte verdadero y esto produce k = + 1.
densidad relativa es una comparación de la densidad de una sustancia con la densidad de otra que se toma como referencia. Ambas densidades se expresan en las mismas unidades y en iguales condiciones de temperatura y presión si la presión y la temperatura son diferentes, entonces las densidades van a cambiar := La densidad relativa es adimensional (sin unidades), ya que queda definida como el cociente de dos densidades.
A veces se la llama densidad específica (del inglés specific density) especialmente en los países con fuerte influencia anglosajona. Tal denominación es incorrecta, por cuanto que en ciencia el término "específico" significa por unidad de masa.
Definición
La densidad relativa o gravedad especifica está definida como el cociente entre la densidad que primordialmente es de una sustancia y la de otra sustancia tomada como referencia, resultando
donde 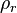 es la densidad relativa,
es la densidad relativa,  es la densidad absoluta y
es la densidad absoluta y  es la densidad de referencia.
es la densidad de referencia.
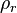 es la densidad relativa,
es la densidad relativa,  es la densidad absoluta y
es la densidad absoluta y  es la densidad de referencia.
es la densidad de referencia.- Para los líquidos y los sólidos, la densidad de referencia habitual es la del agua líquida a la presión de 1 atm y la temperatura de 4 °C. En esas condiciones, la densidad absoluta del agua es de 1000 kg/m3
- Para los gases, la densidad de referencia habitual es la del aire a la presión de 1 atm y la temperatura de 0 °C.
También se puede calcular o medir la densidad relativa como el cociente entre los pesos o masas de idénticos volúmenes de la sustancia problema y de la sustancia de referencia:
Densidad relativa
Es la relación entre el peso específico del cuerpo
y el peso específico de la sustancia de referencia
y el peso específico de la sustancia de referencia
La sustancia de referencia es aire para los gases
y agua para los sólidos y líquidos
y agua para los sólidos y líquidos
| Densidad relativa = | Sc = dr = | gcuerpo | = | rcg | = | rc |
| greferencia | rrg | rr |
La densidad relativa es adimensional:
| [ S ] = | [ F/L3 ] | = 1 |
| [ F/L3 ] |
Densidad relativa del agua: Sa = 1
Densidad relativa - Líquidos y sólidos
Aceite de oliva
|
0.92
|
Cobalto
|
8.90
|
Hulla
|
1.30
|
Platino
|
21.45
| |||
Agua
|
1.00
|
Cobre
|
8.92
|
Iridio
|
22.42
|
Plomo
|
11.34
| |||
Alcohol etílico
|
0.70
|
Cristal
|
3.35
|
Lignito
|
1.20
|
Potasio
|
0.86
| |||
Aluminio
|
2.70
|
Cromo
|
7.14
|
Litio
|
0.53
|
Sal gema
|
2.17
| |||
Antimonio
|
6.71
|
Diamante
|
3.52
|
Magnesio
|
1.74
|
Silicio
|
2.40
| |||
Azufre
|
2.07
|
Estaño
|
7.28
|
Manganeso
|
7.20
|
Sodio
|
0.97
| |||
Benceno
|
0.88
|
Fósforo
|
2.20
|
Mercurio
|
13.55
|
Tungsteno
|
19.32
| |||
Bismuto
|
9.79
|
Glicerina
|
1.26
|
Níquel
|
8.92
|
Uranio
|
18.70
| |||
Calcio
|
1.54
|
Hielo
|
0.91
|
Oro
|
19.30
|
Vidrio
|
2.53
| |||
Cinc
|
7.14
|
Hierro
|
7.88
|
Plata
|
10.50
|
Yodo
|
4.93
|
Densidad relativa - Gases
Aire
|
1.00
|
Hidrógeno
|
0.07
| |
Amoníaco
|
0.60
|
Neón
|
0.70
| |
Argón
|
1.38
|
Nitrógeno
|
0.97
| |
Butano
|
2.00
|
Óxido nitroso
|
1.53
| |
Cloro
|
2.49
|
Monóxido de carbono
|
0.97
| |
Gas carbónico
|
1.53
|
Oxígeno
|
1.10
| |
Helio
|
0.14
|
Ozono
|
1.72
|
No hay comentarios:
Publicar un comentario