Identidades de Green son un conjunto de igualdades en cálculo vectorial. Nombradas así en honor del matemático George Green, el mismo que descubrió el Teorema de Green.
Primera Identidad de Green
Esta identidad se deriva del Teorema de la divergencia aplicado a un campo vectorial  .
.
 .
.
Si  es una función continuamente diferenciable de clase C2 y
es una función continuamente diferenciable de clase C2 y  es otra función continuamente diferenciable, pero de clase C1 en una región U, entonces:
es otra función continuamente diferenciable, pero de clase C1 en una región U, entonces:
 es una función continuamente diferenciable de clase C2 y
es una función continuamente diferenciable de clase C2 y  es otra función continuamente diferenciable, pero de clase C1 en una región U, entonces:
es otra función continuamente diferenciable, pero de clase C1 en una región U, entonces:
donde  es el operador Laplaciano.
es el operador Laplaciano.
 es el operador Laplaciano.
es el operador Laplaciano.Segunda Identidad de Green
Si  y
y  son funciones continuamente diferenciables de clase C2 las dos en U, entonces:
son funciones continuamente diferenciables de clase C2 las dos en U, entonces:
 y
y  son funciones continuamente diferenciables de clase C2 las dos en U, entonces:
son funciones continuamente diferenciables de clase C2 las dos en U, entonces:Tercera Identidad de Green
La tercera identidad de Green se obtiene a partir de la segunda particularizando la función 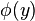 a:
a:
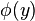 a:
a:
En este caso, el laplaciano de 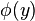 es:
es:
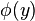 es:
es:
La tercera identidad de Green dice entonces que, si  es una función continuamente diferenciable de clase C2 en U, entonces:
es una función continuamente diferenciable de clase C2 en U, entonces:
 es una función continuamente diferenciable de clase C2 en U, entonces:
es una función continuamente diferenciable de clase C2 en U, entonces:
Donde:
 si
si  ,
, si
si 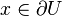 y tiene un plano tangente a
y tiene un plano tangente a 
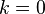 en el resto de casos.
en el resto de casos.
- infinitesimal o infinitésimo se puede definir como una cantidad infinitamente pequeña, se usa en el cálculo infinitesimal, se definen estrictamente como límites y se suelen considerar como números en la práctica.El análisis no estándar introducido en los años 1960 por Abraham Robinson es un enfoque axiomático y riguroso que permite introducir infinitesimales (números hiperreales no nulos cuyo valor absoluto es más pequeño que cualquier número real estándar). Si bien los resultados que pueden lograrse mediante el análisis no estándar pueden ser alcanzados por la teoría estándar de los números reales, existen muchas demostraciones matemáticas y deducciones que son más simples y breves cuando se usan el análisis no estándar. El inverso multiplicativo de un infinitesimal es un número real no estándar ilimitado.
- El cálculo infinitesimal fue propuesto inicialmente por Arquímedes. Luego fue utilizado por Isaac Newton y Gottfried Leibniz, en los albores del surgimiento delAnálisis matemático moderno, pero posteriormente fue desacreditado por George Berkeley y finalmente olvidado. Durante el siglo XIX Karl Weierstrass y Cauchycomenzaron a utilizar la definición formal de límite matemático, por lo que el cálculo infinitesimal ya no era necesario. Sin embargo durante el siglo XX los infinitesimales fueron rescatados como una herramienta que ayuda a calcular límites de forma simple. Es bastante popular el uso de infinitésimos en la bibliografía rusa.Otra manera de trabajar con los infinitésimos es considerarlos como números, y no como límites, es decir trabajar en un conjunto
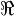 que contenga más números que los usuales. Se les llaman números hiperreales, y son una creación del análisis no estándar.
que contenga más números que los usuales. Se les llaman números hiperreales, y son una creación del análisis no estándar.Análisis estándar
Definición
Un infinitesimal o infinitésimo es una cantidad infinitamente pequeña. Se puede definir matemáticamente como: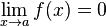 se dice que f es un infinitésimo en x=a
se dice que f es un infinitésimo en x=a
Algunas funciones son infinitésimos en determinados puntos, por ejemplo:- f(x) = x-1 es un infinitésimo en x=1.
- g(x) = sen(x) es un infinitésimo en
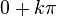 con
con  .
.
Por lo tanto, toda función cuando tiende a 0 en un punto se denomina infinitésima.Propiedades de los infinitésimos
- La suma finita de infinitésimos es un infinitésimo.
- El producto de dos infinitésimos es un infinitésimo.
- El producto de un infinitésimo por una función acotada es un infinitésimo.
- El producto de una constante por un infinitésimo es un infinitésimo.
- La división de un infinitésimo por un escalar no nulo es un infinitésimo
Comparación de infinitésimos
Dadas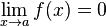 y
y 
- Si
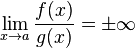 f y g son infinitésimos comparables en x=a y f es un infinitésimo de orden inferior a g en x=a.
f y g son infinitésimos comparables en x=a y f es un infinitésimo de orden inferior a g en x=a. - Si
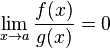 f y g son infinitésimos comparables en x=a y f es un infinitésimo de orden superior a g en x=a.
f y g son infinitésimos comparables en x=a y f es un infinitésimo de orden superior a g en x=a. - Si
 con l perteneciente a
con l perteneciente a  f y g son infinitésimos del mismo orden en x=a.
f y g son infinitésimos del mismo orden en x=a. - En particular, si
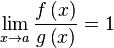 f es un infinitésimo equivalente a g en x=a
f es un infinitésimo equivalente a g en x=a
Si dos infinitésimos son equivalentes entonces se puede aproximar uno a otro. Es decir si f(x) y g(x) son infinitésimos equivalentes cuando entonces se puede decir que
entonces se puede decir que  cuando
cuando  . Si se presentan como factor o divisor pueden sustituirse uno por otro para el cálculo de límites cuando
. Si se presentan como factor o divisor pueden sustituirse uno por otro para el cálculo de límites cuando  .
.Algunos Infinitésimos equivalentes
 es un infinitésimo cuando
es un infinitésimo cuando 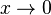 .
. es un infinitésimo cuando
es un infinitésimo cuando 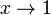 .
.Análisis no estándar
El análisis no estándar es una generalización del análisis real. El análisis no estándar permite definir además de los objetos definibles en la teoría ordinaria de los números reales nuevos objetos denomiandos "externos" o "no estándar". Cualquier objeto (número, conjunto o función) definible en la teoría convencional de los números reales es un objeto "estándar" dentro del análisis no estándar. Junto con los objetos "estándar" el análisis no estándar de Robinson permite introducir "objetos no estándar" como número inifinitesimales o números ilimitados (infinitos) y manejarlos de manera totalmente coherente dentro de la teoría.La teoría no estándar parte de introducir un nuevo predicado , ese predicado permite construir un lenguaje formal que incluye a la teoría ordinaria de los números reales pero permite definir nuevos números (concretamente la noción de número "i-pequeño" e "i-grande" permiten construir números infinitesimales y números ilimitados más grandes que cualquier número real estándar u ordinario). El predicado "estándar" se caracteriza por tres axiomas adicionales que no posee la teoría ordinaria de los números reales, y que por tanto crean un lenguaje formal que permite formalizar números adicionales. El análisis no estándar hace un uso crucial de números infinitesimales e ilimitados:
, ese predicado permite construir un lenguaje formal que incluye a la teoría ordinaria de los números reales pero permite definir nuevos números (concretamente la noción de número "i-pequeño" e "i-grande" permiten construir números infinitesimales y números ilimitados más grandes que cualquier número real estándar u ordinario). El predicado "estándar" se caracteriza por tres axiomas adicionales que no posee la teoría ordinaria de los números reales, y que por tanto crean un lenguaje formal que permite formalizar números adicionales. El análisis no estándar hace un uso crucial de números infinitesimales e ilimitados:- Un número ε es infinitesimal si para cualquier número entero estándar n se cumple que |ε| < 1/n. El único número real estándar con esa propiedad es el cero, pero existe una infinidad r de números reales no estándar tales que: r < 1/n, para cualquier número entero estándar. El predicado inf(·) formaliza la noción de infinitesimal, a partir de la relación primitiva de estándar:
![\mathrm{inf}(r) \Leftrightarrow
\left[\forall n: \mathrm{st}(n) \land \left(-\frac{1}{n}<r<\frac{1}{n} \right)\right]](https://upload.wikimedia.org/math/a/3/4/a347bb3b0599b01824f6c91859f3a8b9.png)
- Análogamente puede definirse un número ilimitado (o infinito) como cualquier número real r tal que r > n para todo número entero estándar. La clave en esa definición es el término estándar, en la teoría ordinaria de los números reales al no existir la noción de estándar no puede formalizarse el concepto de infinito. El predicado Inf(·) formaliza la noción de número ilimitado, a partir de la relación primitiva de estándar:
![\mathrm{Inf}(r) \Leftrightarrow
\left[\forall n: \mathrm{st}(n) \land \left(r<-n \or r>n \right)\right]](https://upload.wikimedia.org/math/f/2/a/f2abbe2d36941269f1bea718eef3e45a.png) El análisis no estándar por tanto permite construir un conjunto de números que extiende al de los números reales, este conjunto es de los números hiperreales y se representa como
El análisis no estándar por tanto permite construir un conjunto de números que extiende al de los números reales, este conjunto es de los números hiperreales y se representa como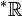 y en él se pueden definirse reglas aritméticas para los números infinitesimales (inf(·)), ilimitados (Inf(·)), limitados (complemento del anterior: ¬Inf(·)) y apreciables (ni infinitesimos, ni ilimitados: ¬inf(·)∧¬Inf(·)), a partir de estos cuatro conjuntos se tienen las siguientes reglas de Leibniz para las operaciones aritméticas de estos conjuntos:
y en él se pueden definirse reglas aritméticas para los números infinitesimales (inf(·)), ilimitados (Inf(·)), limitados (complemento del anterior: ¬Inf(·)) y apreciables (ni infinitesimos, ni ilimitados: ¬inf(·)∧¬Inf(·)), a partir de estos cuatro conjuntos se tienen las siguientes reglas de Leibniz para las operaciones aritméticas de estos conjuntos:+/- infinitesimal limitado apreciable ilimitado infinitesimal infinitesimal limitado apreciable ilimitado limitado limitado limitado limitado ilimitado apreciable apreciable limitado limitado ilimitado ilimitado ilimitado ilimitado ilimitado ?
Para la multiplicación las reglas de Leibniz son las siguientes:x infinitesimal limitado apreciable ilimitado infinitesimal infinitesimal infinitesimal infinitesimal ? limitado infinitesimal limitado limitado ? apreciable infinitesimal limitado apreciable ilimitado ilimitado ? ? ilimitado ilimitado Cálculo infinitesimal
El cálculo infinitesimal o cálculo de infinitesimales constituye una parte muy importante de las matemáticas que estudia conceptos como las funciones, los límites, las derivadas, las integrales, las series infinitas. Es muy habitual en el contexto académico, por comodidad, simplemente llamarlo cálculo.Más concretamente, el cálculo infinitesimal es el estudio del cambio, en la misma manera que la geometría es el estudio del espacio.El cálculo infinitesimal tiene amplias aplicaciones en la ciencia y la ingeniería y nos permite resolver aquellos problemas para los cuales el álgebra por sí sola es insuficiente.El cálculo infinitesimal incluye dos campos principales, cálculo diferencial y cálculo integral, que están relacionados por el teorema fundamental del cálculo. En matemática más avanzada, el cálculo es usualmente llamado análisis matemático, o simplemente análisis, y está definido como el estudio de las funciones.- infinito (símbolo: ∞) aparece en varias ramas de la matemática, la filosofía1 y la astronomía,2 en referencia a una cantidad sin límite o final, contrapuesto al concepto de finitud.3En matemáticas el infinito aparece de diversas formas: en geometría, el punto al infinito en geometría proyectiva y el punto de fugaen geometría descriptiva; en análisis matemático, los límites infinitos; y en teoría de conjuntos como números transfinitos. Todos estos conceptos son diferentes y no corresponden todos ellos a la misma noción de infinitud.
Teoría de conjuntos
Los conjuntos finitos tienen una propiedad "intuitiva" que los caracteriza: "dada una parte propia de los mismos, ésta contiene un número de elementos menor que todo el conjunto". Es decir, no puede establecerse una biyección entre una parte propia del conjunto finito y todo el conjunto. Sin embargo, esa propiedad "intuitiva" de los conjuntos finitos no la tienen los conjuntos infinitos, y formalmente se dice que:Un conjunto es infinito si existe un subconjunto propio
es infinito si existe un subconjunto propio 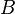 de
de  , es decir, un subconjunto
, es decir, un subconjunto 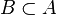 tal que
tal que 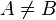 , tal que existe una biyección
, tal que existe una biyección  entre
entre  y
y 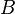 .La idea de cardinalidad de un conjunto se basa en la noción anterior de biyección. De dos conjuntos entre los que se puede establecer una biyección se dice que tienen la misma cardinalidad. Para un conjunto finito su cardinalidad puede representarse por un número natural. Por ejemplo, el conjunto {manzana, pera, durazno} tiene 3 elementos. Esto significa de modo más formal que se puede establecer una biyección entre tal conjunto y el número 3 que es el conjunto {0,1,2}:Dicho de otra forma, es posible hacer parejas (0, manzana), (1, pera), (2, durazno) de modo que cada elemento de los dos conjuntos se utilice exactamente una vez. Cuando es posible establecer tal relación "uno a uno" entre dos conjuntos se dice que ambos conjuntos tienen la misma cardinalidad, lo cual, para conjuntos finitos, equivale a que tengan el mismo número de elementos.
.La idea de cardinalidad de un conjunto se basa en la noción anterior de biyección. De dos conjuntos entre los que se puede establecer una biyección se dice que tienen la misma cardinalidad. Para un conjunto finito su cardinalidad puede representarse por un número natural. Por ejemplo, el conjunto {manzana, pera, durazno} tiene 3 elementos. Esto significa de modo más formal que se puede establecer una biyección entre tal conjunto y el número 3 que es el conjunto {0,1,2}:Dicho de otra forma, es posible hacer parejas (0, manzana), (1, pera), (2, durazno) de modo que cada elemento de los dos conjuntos se utilice exactamente una vez. Cuando es posible establecer tal relación "uno a uno" entre dos conjuntos se dice que ambos conjuntos tienen la misma cardinalidad, lo cual, para conjuntos finitos, equivale a que tengan el mismo número de elementos.Primera definición positiva de conjunto infinito
La primera definición positiva de conjunto infinito fue dada por Georg Cantor y se basa en la siguiente observación: Si un conjunto S es finito y T es un subconjunto propio, no es posible construir una biyección entre S y T. Por ejemplo, si S = {1,2,3,4,5,6,7,8} y T = {2,4,6,8} no es posible construir una biyección entre S y T, porque de ser así tendrían la misma cardinalidad (el mismo número de elementos).Un conjunto es infinito si es posible encontrar un subconjunto propio del mismo que tenga la misma cardinalidad que el conjunto original. Consideremos el conjunto de los números naturales N={1,2,3,4,5,...}, el cual es un conjunto infinito. Para verificar tal afirmación es necesario encontrar un subconjunto propio y construir una biyección entre ambos. Para este caso, consideremos el conjunto de enteros positivos pares P={2,4,6,8,10,...}. El conjunto P es un subconjunto propio de N, y la regla de asignación es una biyección:ya que a todo elemento de N le corresponde un único elemento de P y viceversa.
es una biyección:ya que a todo elemento de N le corresponde un único elemento de P y viceversa.Números ordinales infinitos
Los números ordinales sirven para notar una posición en un conjunto ordenado (primer, segundo, tercer elemento...). El ejemplo más elemental es el de los números naturales, que se definen rigurosamente así: Se nota el conjunto vacío:
el conjunto vacío: se nota
se nota el conjunto que sólo contiene
el conjunto que sólo contiene  :
: luego se nota
luego se nota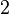 el conjunto que sólo contiene
el conjunto que sólo contiene  y
y  :
: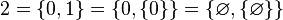 Y así sucesivamente:
Y así sucesivamente: Por construcción, 0 está incluido en 1, quién a su vez está incluido en 2, ya que obviamente:
Por construcción, 0 está incluido en 1, quién a su vez está incluido en 2, ya que obviamente: La inclusión permite convertir a los ordinales en un conjunto bien ordenado (dos elementos distintos siempre se pueden comparar, y añadiendo la igualdad daría un orden total) entre estos conjuntos que se prefiere, por costumbre, escribir "<", lo que da las relaciones 0 < 1 < 2 < 3. Decir que un ordinal es menor (estrictamente) que otro significa, cuando se les considera a ambos como conjuntos, que está incluido en el otro.Si a y b son ordinales, entonces aUb, la unión de los conjuntos, también es un ordinal. En particular, si son ordinales finitos (conjuntos finitos) correspondientes a los naturales a y b, entonces aUb corresponde al mayor de los dos, a o b. En general, si los conjuntos ai son ordinales, donde i toma todos los valores de un conjunto I, entonces a = Uai también lo será. Y si el conjunto I no es finito, tampoco lo será a. Así obtendremos ordinales (o sea números) infinitos.Con el fin de formalizar adecuadamente la discisión, es necesario definir rigurosamente la noción de "infinito", para poderlo aplicar a los ordinales. Dos conjuntos bien ordenados A y B son isomorfos (con relación al orden) si existe una biyección f entre ambos que respeta el orden: si a < a' en A, entonces f(a) < f(a) en B. Resulta obvio constatar que si A es un conjunto ordenado con n elementos (n entero natural) entonces A es isomorfo an = {0, 1, 2, ..., n-1}. Basta con renombrar cada elemento de Apara obtener A = {a0, a1, a2, ..., an-1}. Un isomorfismo es meramente un cambio de apelación. Diremos que un ordinal es finito si cada una de sus partes no vacías tiene un elemento máximo. Por lo tanto todo natural es un ordenal finito. La intuición nos dice que no hay otros ordenales finitos. Lógicamente, diremos que un conjunto ordenado es finito si es isomorfo a un ordinal finito, o sea a un natural.Para introducir los ordinales infinitos, es preciso dar ahora la definición exacta de un ordinal:
La inclusión permite convertir a los ordinales en un conjunto bien ordenado (dos elementos distintos siempre se pueden comparar, y añadiendo la igualdad daría un orden total) entre estos conjuntos que se prefiere, por costumbre, escribir "<", lo que da las relaciones 0 < 1 < 2 < 3. Decir que un ordinal es menor (estrictamente) que otro significa, cuando se les considera a ambos como conjuntos, que está incluido en el otro.Si a y b son ordinales, entonces aUb, la unión de los conjuntos, también es un ordinal. En particular, si son ordinales finitos (conjuntos finitos) correspondientes a los naturales a y b, entonces aUb corresponde al mayor de los dos, a o b. En general, si los conjuntos ai son ordinales, donde i toma todos los valores de un conjunto I, entonces a = Uai también lo será. Y si el conjunto I no es finito, tampoco lo será a. Así obtendremos ordinales (o sea números) infinitos.Con el fin de formalizar adecuadamente la discisión, es necesario definir rigurosamente la noción de "infinito", para poderlo aplicar a los ordinales. Dos conjuntos bien ordenados A y B son isomorfos (con relación al orden) si existe una biyección f entre ambos que respeta el orden: si a < a' en A, entonces f(a) < f(a) en B. Resulta obvio constatar que si A es un conjunto ordenado con n elementos (n entero natural) entonces A es isomorfo an = {0, 1, 2, ..., n-1}. Basta con renombrar cada elemento de Apara obtener A = {a0, a1, a2, ..., an-1}. Un isomorfismo es meramente un cambio de apelación. Diremos que un ordinal es finito si cada una de sus partes no vacías tiene un elemento máximo. Por lo tanto todo natural es un ordenal finito. La intuición nos dice que no hay otros ordenales finitos. Lógicamente, diremos que un conjunto ordenado es finito si es isomorfo a un ordinal finito, o sea a un natural.Para introducir los ordinales infinitos, es preciso dar ahora la definición exacta de un ordinal:- Un conjunto A totalmente ordenado (por la inclusión) es un ordinal si y sólo si cada elemento de A es también un subconjunto de A
Ya vimos que es el caso para los naturales: Por ejemplo, el conjunto 2 = {0, 1} admite 1= {0}, como elemento y por lo tanto también como subconjunto.Todo conjunto bien ordenado es isomorfo a un ordinal. Esto es obvio en el caso finito, y se muestra por inducción transfinita que lo es en el caso infinito. O sea, renombrando los elementos de un conjunto bien ordenado siempre obtenemos un ordinal.Primer ordinal infinito
Ya hemos visto que una unión cualquiera de ordinales es un ordinal. Si tomamos una unión finita de ordinales finitos, fabricamos un ordinal finito. Para obtener el primer ordinal infinito tenemos que reunir un número no finito de ordinales finitos. Haciéndolo, siempre caemos en el mismo conjunto, construido al reunir todos los ordinales finitos, es decir los naturales. El conjunto de todos los naturales, ℕ, es pues el primer ordinal infinito, lo que no debería sorprender, y lo notamos en este contexto ω (omega).Para visualizar los ordinales, resulta muy práctico representar cada uno por un punto de una sucesión creciente convergente, como por ejemplo un = 1 - 1/(n+1). Esto da algo semejante a:- X__________X_________X_______X______X______X_____X____X___X__X_X_XXX........
Escojamos un punto de la sucesión, y miremos cuantos puntos están más a la izquierda. En el ejemplo, hay cuatro, y por lo tanto se trata de u4, lo que corresponde al ordinal 4. Para representar el ordinal w, resulta natural añadir a la sucesión previa un punto 'O' situado exactamente en el límite de la sucesión:- X__________X_________X_______X______X______X_____X____X___X__X_X_XXX...O
A la izquierda de uw hay una infinidad de puntos, por lo tanto w es infinito. Pero si elegimos a cualquier otro punto de la sucesión a su izquierda, ya no es el caso, lo cual prueba que w es el primer ordinal infinito. Después de w llega w+1, w+2 ... que se representan añadiendo a la derecha uno dos o más puntos, inicialmente distantes, y luego más cercanos entre sí:- X________X________X_______X______X______X_____X____X___X__X_X_XXX...O_______X_____X
El último punto dibujado corresponde a w+2.Más generalmente, para sumar dos ordinales A y B se cambian los nombres de los elementos para que sean todos distintos, luego se juntan los conjuntos A y B, poniendo B a la derecha de A es decir imponiendo que cada elemento de B sea mayor que todos los de A. Así hemos construido w+1, ... y así podemos construir 1+w: Notemos Y el elemento de 1, y X los de w:- Y__________X__________X_________X_______X______X______X_____X____X___X__X_X_XXX...
Salta a la vista que w y 1+w son muy parecidos. De hecho la función x →x - 1 realiza un isomorfismo entre ellos (1+w tiene dos elementos llamados 0: 0A y 0B. El primero hace el papel de -1 en la función). Por lo tanto corresponden al mismo ordinal: 1+w = w. Mas no es el caso de w+1, que es distinto de w porque su el conjunto w+1 tiene un elemento máximo (el O del dibujo) mientras que el conjunto w no lo tiene (el límite de los naturales no es un natural).El punto w (el O del dibujo) no tiene antecesor, es decir que no existe un n tal que n+1=w: se dice que w es un ordinal límite. Cero tiene también esta propiedad pero no merece esta apelación. Como w+1 ≠ 1+w, la adición no es conmutativa en los ordinales.Se construye del mismo modo w + w que se nota lógicamente 2w. La multiplicación se define a partir de la adición como para los naturales.Una vez que se ha representado nw, con n natural, no resulta demasiado difícil imaginar lo que será w.w, escrito w2. Luego se puede definir wn, con n natural, y, tomando el límite, ww, tiene tantos elementos como la recta real.La sucesión tiene como límite
tiene como límite 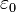 .
.Números cardinales infinitos
El cardinal de un conjunto es el número de elementos que contiene. Esta noción es por lo tanto distinta del ordinal, que caracteriza el lugar de un elemento en una sucesión. "Cinco" difiere de "quinto" aunque obviamente existe una relación entre ambos. Se dice que dos conjuntos tienen el mismo cardinal si existe una biyección entre ellos. Contrariamente a los ordinales, esta biyección no tiene que respetar el orden (además los conjuntos no tienen que ser ordenados).Como ya tenemos un surtido de conjuntos -los ordinales- veamos sus tamaños (o sea sus cardinales) respectivos. No es ninguna sorpresa que los ordinales finitos también son cardinales: entre dos conjuntos con n y m elementos, m y n distintos, no puede haber biyección, por lo tanto tienen cardinales distintos. Pero no es el caso con los ordenales infinitos: Por ejemplo, y
y 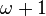 están en biyección por la función:
están en biyección por la función:
 y
y  , tal biyección no respeta el orden, por eso dos ordinales distintos pueden corresponder a un mismo cardinal.
, tal biyección no respeta el orden, por eso dos ordinales distintos pueden corresponder a un mismo cardinal.
Se suele notar |A| el cardinal de A. Se llama (alef0) el cardinal de w, o sea del conjunto de los naturales (donde alef es la primera letra del alfabeto hebreo).Si A y B son conjuntos, entonces
(alef0) el cardinal de w, o sea del conjunto de los naturales (donde alef es la primera letra del alfabeto hebreo).Si A y B son conjuntos, entonces , donde x designa el producto cartesiano de los conjuntos, y "·" es el producto de los cardinales definidos por esta fórmula. El conjunto de las partes de un conjunto A, P(A) está en biyección con el conjunto de las funciones de A hacia {0,1}, conjunto que de escribe como 2A, como caso particular de YX que denota el conjunto de las aplicaciones de X hacia Y.El cardinal de R, conjunto de los reales, es por lo tanto 2alef0, porque R está en biyección con las partes de N, por medio de la escritura decimal de los reales.No se puede decidir, con los axiomas clásicos (los de la teoría de los conjuntos, fundamentos de la matemática), si existe un cardinal mayor que alef0 y menor que 2alef0, es decir si existe un conjunto con más elementos que N pero con menos elementos que R. La hipótesis del continuo, que es un axioma adicional, afirma que no.
, donde x designa el producto cartesiano de los conjuntos, y "·" es el producto de los cardinales definidos por esta fórmula. El conjunto de las partes de un conjunto A, P(A) está en biyección con el conjunto de las funciones de A hacia {0,1}, conjunto que de escribe como 2A, como caso particular de YX que denota el conjunto de las aplicaciones de X hacia Y.El cardinal de R, conjunto de los reales, es por lo tanto 2alef0, porque R está en biyección con las partes de N, por medio de la escritura decimal de los reales.No se puede decidir, con los axiomas clásicos (los de la teoría de los conjuntos, fundamentos de la matemática), si existe un cardinal mayor que alef0 y menor que 2alef0, es decir si existe un conjunto con más elementos que N pero con menos elementos que R. La hipótesis del continuo, que es un axioma adicional, afirma que no.Análisis matemático
Análisis estándar u ordinario
Un conjunto de números reales S es acotado superiormente si existe un número c (la cota) tal que c es mayor que todo elemento de S (Por ejemplo, si S={π ; 7 ;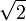 } entonces S es un conjunto acotado, ya que el número c=10 cumple que π<10 7="" alt="\sqrt{2} \,\!" class="mwe-math-fallback-image-inline tex" img="" nbsp="" src="https://upload.wikimedia.org/math/7/3/7/737429de3cfb42c6e623818e7fa5afb2.png" style="border: none; display: inline-block; page-break-inside: avoid; vertical-align: middle;"><10 acotado="" conjunto="" cualquier="" cuando="" es="" i="" mero="" n="" nbsp="" no="" para="" un="">c
} entonces S es un conjunto acotado, ya que el número c=10 cumple que π<10 7="" alt="\sqrt{2} \,\!" class="mwe-math-fallback-image-inline tex" img="" nbsp="" src="https://upload.wikimedia.org/math/7/3/7/737429de3cfb42c6e623818e7fa5afb2.png" style="border: none; display: inline-block; page-break-inside: avoid; vertical-align: middle;"><10 acotado="" conjunto="" cualquier="" cuando="" es="" i="" mero="" n="" nbsp="" no="" para="" un="">c
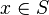 de modo que c < x. El concepto de infinito se introduce como una cota especial para este tipo de conjuntos. Este concepto de infinito se representa con el símbolo
de modo que c < x. El concepto de infinito se introduce como una cota especial para este tipo de conjuntos. Este concepto de infinito se representa con el símbolo  .
.
También es utilizado en el Análisis matemático cuando se quiere expresar que los términos de una sucesión ordenada, o los valores que toma una función al tomar la variable dependiente valores cercanos a uno fijado previamente "diverge" ("tiende a infinito", o su límite es infinito). En este contexto, se considera  para representar al límite que tiende a infinito y
para representar al límite que tiende a infinito y  al límite cuando tiende a 0; y no al número 0).
al límite cuando tiende a 0; y no al número 0).
 para representar al límite que tiende a infinito y
para representar al límite que tiende a infinito y  al límite cuando tiende a 0; y no al número 0).
al límite cuando tiende a 0; y no al número 0).
Para recordar las reglas de límite se suele entonces acudir a las siguientes reglas nemotecnias: (aquí "x" representa un n° real cualquiera)
-
 ,
, 
-
- Si
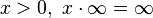 y
y 
- Si
 y
y 
- Si
Las identidades anteriores son perfectamente formalizables en el análisis no estándar asociado a los números hiperreales.
Límites indeterminados (no es posible determinar a priori su valor como en el resto de los ejemplos, no hay un valor asignado):
Análisis no estándar
El análisis no estándar amplia la teoría de los números reales. Desde el punto de vista lógico los números reales pueden ser entendidos como un lenguaje formal en el que se da por supuesto la existencia de ciertos objetos y en el cual se puede deducir la existencia de otros objetos. En términos de lenguajes formales el análisis no estándar es una extensión lógica de la teoría ordinaria de los números reales que además es conservadora (en el sentido que sus teoremas deducibles coinciden con los deducibles en la teoría ordinaria de los números reales). Si bien esta extensión parece antieconómica desde el punto de vista de la navaja de Ockham, ya que la complicación introducida no altera la clase de teoremas básicos sobre los números reales ordinarios, realmente permite hacer demostraciones más breves, derivar resultados más fácilmente que en la teoría ordinaria y frecuentemente más intuitiva en términos lógicos.
En el seno del análisis no estándar se introduce un predicado nuevo st(·) y tres nuevos axiomas que describen el uso de dicho predicado. Gracias a ese predicado el conjunto de números descritos por el lenguaje forman se puede dividir en "elementos estándar" para los cuales (r es estándar si st(r) es cierto) y "elementos no estándar" (r es no estándar si ¬st(r) es cierto). Los elementos estándar tienen esencialmente las mismas propiedades que los números reales ordinarios, mientras que los elementos no estándar incluyen números especiales algunos de los cuales como infinitesimales o como números ilimitados (infinitos). La ventaja de la estructura lógica del análisis no estándar es que se pueden usar dichos números y ser empleados en deducciones sin inconsistencia alguna (a diferencia de las reglas heurísticas del cálculo infinitesimal tradicional antes de la formalización del siglo XIX).
En el análisis no estándar pueden definirse números que intuitivamente se comportan como números infinitos gracias al predicado st(·) "· es estándar". Por ejemplo un número ilimitado r satisface que "para cualquier número e del conjunto y cualquier número natural estándar resulta que ne < r", formalmente:
Obviamente el número r no puede ser estándar, ya que para números estándar se tiene que "para cualquier número e y cualquier r existe un natural tal que ne > r, formalmente:
Nótese que en esta expresión no aparece el predicado "estándar" st(·), y por tanto es formalizable en la teoría ordinaria, mientras que la noción de número ilimitado no es formalizable en la teoría ordinaria por carecer esta teoría del predicado st(·).
Análogamente en el análisis no estándar pueden definirse números infinitesimales, más pequeños en valor absoluto que cualquier número estándar positivo. De hecho el inverso de un número ilimitado es siempre un número infinitesimal.
Infinito en informática
De manera relacionada con el infinito para números reales, algunos lenguajes de programación admiten un valor especial que recibe el nombre de infinito: valor que se puede obtener como resultado de ciertas operaciones matemáticas no realizables, tales como las descritas en el punto anterior u operaciones teóricamente posibles, pero demasiado complejas para su trabajo en el ordenador/lenguaje en cuestión. En otros lenguajes simplemente se produciría un error.
Infinito en metafísica
Lo infinito no puede admitir ninguna restricción, lo que supone que es absolutamente incondicionado e indeterminado, ya que toda determinación, cualquiera que sea, es forzosamente una limitación, por eso mismo de que deja algo fuera de ella. Por otra parte, la limitación presenta el carácter de una verdadera negación: poner un límite, es negar, para lo que está encerrado en él, todo lo que este límite excluye; por consiguiente, la negación de un límite es propiamente la negación de una negación, es decir, lógica e incluso matemáticamente una afirmación, de tal suerte que la negación de todo límite equivale en realidad a la afirmación total y absoluta. Lo que no tiene límites, es aquello de lo cual no se puede negar nada, y por consiguiente, aquello que contiene todo, aquello fuera de lo cual no hay nada; y esta idea del Infinito, que es así la más afirmativa de todas, puesto que comprende o envuelve todas las afirmaciones particulares, cualesquiera que puedan ser, no se expresa por un término de forma negativa (in-finito) sino en razón misma de su indeterminación absoluta.4
Historia
El símbolo de infinito
El símbolo  con que se expresa el infinito fue introducido a la notación matemática por el matemático inglés John Wallis (1616-1703) en una de sus obras más importantes: Aritmética Infinitorum en 1656. En 1694 fue creada la representación gráfica lemniscatapor Jacob Bernoulli (1655-1705).5
con que se expresa el infinito fue introducido a la notación matemática por el matemático inglés John Wallis (1616-1703) en una de sus obras más importantes: Aritmética Infinitorum en 1656. En 1694 fue creada la representación gráfica lemniscatapor Jacob Bernoulli (1655-1705).5
 con que se expresa el infinito fue introducido a la notación matemática por el matemático inglés John Wallis (1616-1703) en una de sus obras más importantes: Aritmética Infinitorum en 1656. En 1694 fue creada la representación gráfica lemniscatapor Jacob Bernoulli (1655-1705).5
con que se expresa el infinito fue introducido a la notación matemática por el matemático inglés John Wallis (1616-1703) en una de sus obras más importantes: Aritmética Infinitorum en 1656. En 1694 fue creada la representación gráfica lemniscatapor Jacob Bernoulli (1655-1705).5
También se cree posible que la forma provenga de otros símbolos alquímicos o religiosos, como por ejemplo ciertas representaciones de la serpiente uróboros.
Se ha querido ver también una banda de Möbius en su forma, aunque el símbolo se usó durante cientos de años antes de que August Möbius descubriera la banda que lleva su nombre.
El símbolo de infinito se representa en Unicode con el carácter ∞ (U+221E).
| Año | Acontecimiento |
|---|---|
| 350 a.C. | Aristóteles rechaza un infinito real. |
| 1639 | Gérard Desargues introduce la idea del infinito en la geometría. |
| 1655 | Se atribuye a John Wallis haber sido el primero en utilizar el símbolo  para el infinito. para el infinito. |
| 1874 | Georg Cantor especifíca, en la teoría de conjuntos, distintos órdenes de infinito. |


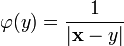
![\oint_{\partial U} \left[\frac{1}{|\mathbf{x} - y|} \frac{\partial}{\partial n}\psi(\mathbf{y}) - \psi(\mathbf{y})\frac{\partial}{\partial n_\mathbf{y}} \frac{1}{|\mathbf{x} - y|}\right]\, dS_\mathbf{y} - \int_U \left[\frac{1}{|\mathbf{x} - y|} \Delta\psi(\mathbf{y})\right]\, dV_\mathbf{y} = k.](https://upload.wikimedia.org/math/5/b/b/5bbf83c3fee86a97b8a497b513ae2127.png)
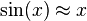
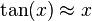


















![\forall e\in{}^*\R, \forall n\in \mathbb{N}, \left[ \mathrm{st}(n) \land ne < r \right]](https://upload.wikimedia.org/math/6/3/c/63c46554bb7b91bb9408dae0b641c277.png)
![\forall e\in{}^*\R, \exists n\in \mathbb{N}, \left[ ne > r \right]](https://upload.wikimedia.org/math/7/2/6/72625e2d6975194dce6124eb971774f5.png)

No hay comentarios:
Publicar un comentario