función de decrecimiento rápido es una función f sobre  que decrece a cero hacia infinto de tal manera que, su cota superior asintótica cumple que:
que decrece a cero hacia infinto de tal manera que, su cota superior asintótica cumple que:
 que decrece a cero hacia infinto de tal manera que, su cota superior asintótica cumple que:
que decrece a cero hacia infinto de tal manera que, su cota superior asintótica cumple que:
El conjunto de estas funciones puede convertirse en un espacio normado, llamado espacio de Schwartz.
Una función gaussiana bidimensional es un ejemplo de función de decrecimiento rápido, y por tanto, un elemento del espacio de Schwartz.
función de Dirichlet, llamada así en honor al matemático alemán Peter Gustav Lejeune Dirichlet, es una función matemática especial, que tiene la peculiaridad de no ser continua en ningún punto de su dominio.
Si c y d son dos números reales con c ≠ d, (usualmente se toman los valores c = 1 y d = 0), la función de Dirichlet se define como:
Analíticamente, se puede representar de la siguiente manera:
Esta función es discontinua en todo punto de su dominio.
Función de Dirichlet
La función de Dirichlet es una función real de variable real que no es continua en ningún punto de la recta. Se define de la siguiente forma:
Vamos a demostrar que esta función no es continua en ningún punto usando lacaracterización de continuidad por sucesiones, que dice lo siguiente:
Seauna función real de variable real y sea
. Entonces f es continua en a si
sucesión de elementos de A tal que
se tiene que
Por tanto f no es continua en a sisucesión de elementos de A tal que
pero
Sea  . Por ser
. Por ser  denso en
denso en  se tiene que existirá una sucesión
se tiene que existirá una sucesión  tal que
tal que  . Y aquí está el problema: como
. Y aquí está el problema: como  se tiene que
se tiene que  y como
y como  se tiene que
se tiene que  . Por tanto
. Por tanto  .
.
Al ser  también denso en
también denso en  la demostración para el caso
la demostración para el caso  es análoga a la anterior. Por tanto f(x) no es continua en ningún punto.
es análoga a la anterior. Por tanto f(x) no es continua en ningún punto.
En general, si en vez de tomar  tomamos cualquier subconjunto
tomamos cualquier subconjunto  que sea densoen
que sea densoen  tenemos una función que no es continua en ningún valor real.
tenemos una función que no es continua en ningún valor real.
En análisis matemático, partiendo de una función real de valores reales f, definida en una vecindad de x = b, diremos que f es una función semicontinua inferiormenteen x = b si para todo ε > 0 existe un δ > 0, de tal manera que de las condiciones |x - b|< δ y x elemento del dominio de f, se deducen que f(x)≥ f(b) - ε.1
Análogamente, podría ser definida una función semicontinua superiormente en x= c si para todo ε > 0 existe un δ > 0, de tal manera que de las condiciones |x - c|< δ y x elemento del dominio de f, se deducen que f(x)≤ f(c) - ε.
identidad de Euler a un caso especial de la fórmula desarrollada por Leonhard Euler, notable por relacionar cinco números muy utilizados en la historia de lasmatemáticas y que pertenecen a distintas ramas de la misma:
donde:
- π (número pi) es un número irracional y trascendente que relaciona la longitud de la circunferencia con su diámetro y está presente en varias de las ecuaciones más fundamentales de la física.

- e (número de Euler) es la suma de la serie
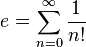 , que aparece en numerosos procesos naturales y en diferentes problemas físicos y matemáticos y es también un número irracional y trascendente.
, que aparece en numerosos procesos naturales y en diferentes problemas físicos y matemáticos y es también un número irracional y trascendente. - i (unidad imaginaria) es la raíz cuadrada de -1, a partir del cuál se construye el conjunto de los números complejos.
- 0 y 1 son los elementos neutros respectivamente de la adición y la multiplicación
Esta identidad se puede emplear para calcular π:

- La identidad es un caso especial de la Fórmula de Euler, la cual especifica quepara cualquier número real x. (Nótese que los argumentos para las funciones trigonométricas sen y cos se toman enradianes.) En particular sientoncesy ya quey quese sigue queLo cual implica la identidad
Para una forma alternativa de notar que la identidad de Euler es tanto verdadera como profunda, supongamos que:en el desarrollo polinómico de e a la potencia x:para obtener:simplificando (usando i2 = -1):Al separar el segundo miembro de la ecuación en subseries real e imaginarias:Se puede comprobar la convergencia de estas dos subseries infinitas, lo cual implicaLogaritmos de números negativos
Durante la historia ha habido disputas sobre cómo calcular los logaritmos de números negativos. Gracias a la identidad de Euler, dicha disputa ha sido zanjada. Si queremos calcular, por ejemplo, podemos proceder de la siguiente manera:Sabiendo que
podemos proceder de la siguiente manera:Sabiendo que :
:
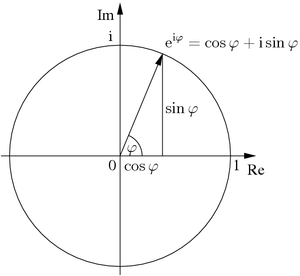 Fórmula de Euler para un ángulo general.
Fórmula de Euler para un ángulo general.- Un número complejo es aquél que se representa mediante una parte real y una parte imaginaria, si definimos a z como un complejo, x su parte real e y su parte imaginaria, este quedaría así,

Donde i es el número imaginario, definido como la raíz cuadrada de -1,
Ahora, si tomo al famoso numero e y lo potencio con el número complejo z,
Mediante series numéricas, Euler encontró que,
Por lo tanto,
Esta es conocida como la fórmula de Euler, que define la exponenciación compleja. Es una fórmula de gran sutileza y precisión. Pero si hacemos un análisis más minucioso podemos llegar a más aún.
Si hacemos que x valga 0 y que y tome el valor de pi,
A su vez, sabemos que el seno de pi es cero y el coseno de pi vale -1, entonces,
Ó, resulta lo mismo escribir,
Esta es la identidad de Euler, la ecuación más famosa de la matemática. En ella se puede decir que está resumida toda la matemática. Encontramos los conceptos de suma, multiplicación, exponenciación e identidad. Tenemos también, los cinco números fundamentales, el cero, el uno, pi, el número e y el número i.
Esta ecuación expresa con unos pocos símbolos matemáticos, una belleza infinita. Digna de un genio como Euler.







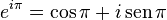










No hay comentarios:
Publicar un comentario