matriz hessiana o hessiano de una función f de n variables, es la matriz cuadrada de n × n, de las segundas derivadas parciales.
Si todas las segundas derivadas parciales de f existen, se define la matriz hessiana de f como:
 , donde
, donde .
.
tomando la siguiente forma
Además, se tiene que si :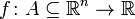 con A un conjunto abierto y f clase
con A un conjunto abierto y f clase  , entonces la matriz hessiana está bien definida, y en virtud del teorema de Clairaut(ó teorema de Schwarz), es una matriz simétrica.
, entonces la matriz hessiana está bien definida, y en virtud del teorema de Clairaut(ó teorema de Schwarz), es una matriz simétrica.
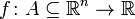 con A un conjunto abierto y f clase
con A un conjunto abierto y f clase  , entonces la matriz hessiana está bien definida, y en virtud del teorema de Clairaut(ó teorema de Schwarz), es una matriz simétrica.
, entonces la matriz hessiana está bien definida, y en virtud del teorema de Clairaut(ó teorema de Schwarz), es una matriz simétrica.
Esta matriz debe su nombre al matemático alemán Ludwig Otto Hesse y fue introducido por James Joseph Sylvester.
Aplicación de la matriz hessiana
Concavidad/Convexidad
Sea  un conjunto abierto y
un conjunto abierto y 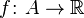 una función con segundas derivadas continuas:
una función con segundas derivadas continuas:
 un conjunto abierto y
un conjunto abierto y 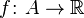 una función con segundas derivadas continuas:
una función con segundas derivadas continuas: es convexa si y solo si,
es convexa si y solo si,  , la matriz hessiana
, la matriz hessiana 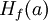 es positiva-definida.
es positiva-definida.- Si
 la matriz hessiana
la matriz hessiana 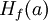 es positiva-definida, entonces
es positiva-definida, entonces  es estrictamente convexa.
es estrictamente convexa.- Si
 es una función convexa, entonces cualquier punto en que todas las derivadas parciales son cero, es un mínimo local.
es una función convexa, entonces cualquier punto en que todas las derivadas parciales son cero, es un mínimo local.
- Si
 es cóncava si y solo si,
es cóncava si y solo si,  , la matriz hessiana
, la matriz hessiana 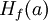 es negativa-definida.
es negativa-definida.- Si
 la matriz hessiana
la matriz hessiana 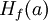 es negativa-definida, entonces f es estrictamente cóncava.
es negativa-definida, entonces f es estrictamente cóncava.- Si
 es una función cóncava, entonces cualquier punto en que todas las derivadas parciales son cero, es un máximo local.
es una función cóncava, entonces cualquier punto en que todas las derivadas parciales son cero, es un máximo local.
- Si
Método para determinar el carácter de los puntos críticos
Se verá a continuación cómo hallar los puntos críticos (máximos, mínimos y puntos de inflexión -o silla o de ensilladura) de una función f de múltiples variables.
- Se igualan las derivadas parciales primeras a cero.
- Se resuelven las ecuaciones anteriores y se obtienen las coordenadas de los puntos críticos.
- Se construye la matriz hessiana (derivadas segundas parciales).
- Se sustituyen los puntos críticos en la matriz hessiana para obtener tantas matrices como puntos críticos tengamos.
- Dependiendo del tipo de matriz resultante de evaluar la matriz Hessiana en los diferentes puntos críticos, estos puntos se pueden evaluar mediante el criterio de Sylvester:
-
- Si todos los menores principales son mayores que 0, o sea, |Hi|>0 ∀i=1,...,n ƒ alcanza el mínimo relativo en el punto.
- Si los menores principales de índice par son mayores que 0 y los de índice impar son menores que 0, o sea, |Himpar|<0 i="" y="">H
- Cuando algún |Hi|=0 no se puede determinar nada, por lo que hace un estudio particular. Para n=2. el criterio se mejora en el sentido de que si |H1|=0 y |H2|<0 dd="" de="" el="" en="" punto.="" punto="" silla="" tiene="" un="">
De forma análoga podemos evaluar los extremos relativos de un campo escalar f:R^n--->R estudiando los autovalores de su matriz hessiana.
Teorema 9.6(CALCULUS volumen 2. Tom M.Apostol): "Sea f un campo escalar con derivadas parciales segundas continuas Dijf en una n-bola B(a), y designemos con H(a) la matriz hessiana en el punto estacionario a. Tenemos entonces:
a)Si todos los autovalores de H(a) son positivos, f tiene un mínimo relativo en a.
b)Si todos los autovalores de H(a) son negativos, f tiene un máximo relativo en a.
c)Si H(a) tiene autovalores positivos y negativos, f tiene un punto de ensilladura en a."
El el caso particular en el que la función a evaluar grafica una superficie en R^3, f(x,y)=z, y tiene segundas derivadas continuas, se pueden estudiar los puntos críticos evaluando la matriz hessiana en ellos y luego utilizando el criterio de determinación de extremos. Si (a,b) es un punto crítico de f, (fx(a,b)=0 y fy(a,b)=0) entonces:
- Si el determinante de la matriz hessiana evaluado en el punto (a,b) es mayor que 0, |H|>0, y fxx(a,b)<0 i="">, decimos que f alcanza un máximo relativo en(a,b).
- Si el determinante de la matriz hessiana evaluado en el punto (a,b) es mayor que 0, |H|>0, y fxx(a,b)>0, decimos que f alcanza un mínimo relativo en(a,b).
- Si el determinante de la matriz hessiana evaluado en el punto (a,b) es menor que 0, |H|<0 decimos="" i="" nbsp="" que="">f(a,b)
es un Punto de silla.
- Si el determinante de la matriz hessiana evaluado en el punto (a,b) es igual a 0, |H|=0, el criterio no concluye resultado alguno.
Generalizaciones
Matriz hessiana orlada
La matriz hessiana orlada es una variante de la matriz hessiana utilizada en problemas de optimización restringida. El determinante de sus principales menores se utiliza como criterio para determinar si un punto crítico de una función es un mínimo, máximo, punto silla o no determinado (extremos condicionados).1
Aplicación bilineal hessiana
El concepto de matriz hessiana puede generalizarse a espacios de dimensión infinita, concretamente a aplicaciones definidas sobre espacios vectoriales normados. Si una aplicación (o funcional) está definida es diferenciable en el sentido de Fréchet y su diferencial jacobiana también es diferenciable en el sentido de Fréchet puede definirse una forma bilineal continua (y por tanto acotada) sobre el espacio normado que generaliza la matriz hessiana.
Se dice que una aplicación 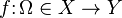 entre espacios vectoriales normados
entre espacios vectoriales normados 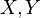 es diferenciable si existe una aplicación lineal continua
es diferenciable si existe una aplicación lineal continua 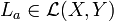 tal que:
tal que:
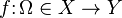 entre espacios vectoriales normados
entre espacios vectoriales normados 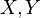 es diferenciable si existe una aplicación lineal continua
es diferenciable si existe una aplicación lineal continua 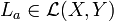 tal que:
tal que:
En ese caso se escribe:
Puede probarse que  es a su vez otro espacio vectorial normado con la norma:
es a su vez otro espacio vectorial normado con la norma:
 es a su vez otro espacio vectorial normado con la norma:
es a su vez otro espacio vectorial normado con la norma:
La segunda derivadas cuando existe es:
La forma bilineal hessiana viene dada por:
NOTACIÓN EN DERIVADAS PARCIALES
Primeramente se aclaran las notaciones que se pueden utilizar y que representan lo mismo al trabajar con derivadas parciales:
Si tenemos un ejercicio con dos variables, obtendremos una matriz hessiana 2 x 2. Si el ejercicio fuera de tres variables, la matriz gesiana será 3 x 3, y así sucesivamente. Para el caso de dos variables, la matriz hessiana 2 x 2 se genera de la siguiente manera:
En este trabajo se estará usando la notación que aparece en el miembro izquierdo de las ecuaciones por considerarlo más sencillo de comprender a primera vista.
Antes de presentar ejemplos, se muestra la matriz resultante cuando se trabaja con ejercicios o problemas de tres variables. La matriz hessiana será de 3 x 3 y queda de esta forma:
Con el objetivo de explicar cada detalle con la mayor claridad posible, se expresa el significado de cada uno de los elementos que aparecen dentro de la matriz:
NOTA: Es bueno tomar en cuenta que:
Ya se presentó la matriz hessiana de 2 variables y de 3 variables. Sin embargo podemos enfrentarnos a problemas en los que hayan más de tres variables, para lo cual se presenta a continuación lo que se tiene que hacer cuando se tengan matrices hessianas de cuatro variables o más, osea matrices 4 x 4, 5 x 5, 6 x 6, etc.
La manera de resolver este tipo de problemas de más de dos variables se presenta con la siguiente matriz, y funciona para cualquier problema donde se utilice matriz hessiana con más de dos variables:
Antes de continuar se debe decir que para ser capaces de resolver problemas utilizando matrices hessianas se debe poder resolver sin problemas determinantes cuadradas, pues es algo que se utiliza al trabajar con matrices. En este trabajo no se explica cómo resolver determinantes cuadradas pero se aclara que es algo indispensable en el trabajo y resolución de problemas utilizando matrices hessianas.
1. Tener la función original que se va a trabajar.
2. Calcular las primeras derivadas parciales de la función con respecto a cada una de las variables que se tiene la función original.
3. Igualar a cero las primeras derivadas que se calcularon en el paso 2.
4. Simultanear las ecuaciones generadas en el paso 3 para encontrar el valor de cada una de las variables. Esos valores encontrados para cada una de las variables serán las coordenadas de los puntos críticos.
5. Teniendo los puntos críticos que se encontraron en el paso 4, se tiene que calcular las segundas derivadas parciales en el punto crítico de modo que asignemos los valores de cada elemento de la matriz hessiana, ya sea matriz 2 x 2 (si la función es de 2 variables), 3 x 3 (si la función es de 3 variables), 4 x 4 (si la función es de 4 variables), n x n (si la función es de n variables).
6. Resolver la matriz hessiana normalmente como se resuelve la determinante de una matriz cuadrada. El resultado que se obtenga de la matriz hessiana es la respuesta.
7. Se sacan conclusiones de la respuesta obtenida en el paso 6 de la siguiente manera:
CASO DE DOS VARIABLES O MATRIZ HESSIANA 2 X 2:
- Si el determinante de la matriz hessiana es mayor que cero, entonces se procede a ver si
es positivo o negativo. Si
es positivo o mayor que cero entonces la función tiene un MÍNIMO en el punto crítico. Si
es negativo o menor que cero entonces la función tiene un MÁXIMO en el punto crítico.
- Si el determinante de la matriz hessiana es menor que cero entonces se concluye que la función tiene un PUNTO DE SILLA en el punto crítico.
- Si el determinante de la matriz hessiana es cero entonces se concluye que NO HAY INFORMACIÓN o EL CRITERIO NO ES CONCLUYENTE.
CASO DE TRES O MÁS VARIABLES O MATRIZ HESSIANA 3 X 3 O N X N:
- Si todos los determinantes de la matriz hessiana tienen signo positivo, entonces la función tiene un MÍNIMO en el punto crítico.
- Si los determinantes tienen signo alterno (comenzando con un valor negativo), entonces la función tiene un MÁXIMO en el punto crítico.
- Si no se cumple lo dicho en los literales a) y b), osea en cualquier otro caso se concluye que HAY DUDA, NO HAY INFORMACIÓN o EL CRITERIO NO ES CONCLUYENTE.
NOTA: En el caso de tener funciones de tres o más variables significa que comenzaremos trabajando la matriz hessiana f(x) o de 1 x 1, luego f(x,y) o de 2 x 2, luego f(x,y,z) o de 3 x 3,… hasta llegar a f(x,y,z,…n) o de n x n. Así llegaremos finalmente a concluir si se trata de máximo, mínimo o si no se sabe, de acuerdo a los tres literales anteriores.
Encontrar los máximos y mínimos (si los hay) de la función:
f(x,y,z) = x² + y² + 7z² - xy
Solución:
Calculando las primeras derivadas parciales de la función con respecto a cada una de las variables que tiene la función original:
Igualando a cero las primeras derivadas:
22x – y = 0
2y – x = 0
14z = 0
Simultanear las ecuaciones anteriores para encontrar los valores de x, y y z, que serán las coordenadas de los puntos críticos:
Al simultanear las ecuaciones obtenemos que los valores de x, y y z (osea los puntos críticos) son:
x = 1/3
y = 2/3
z = 0
Esto significa que las coordenadas del punto crítico son: f(1/3,2/3,0).
Calcular las segundas derivadas en el punto crítico para generar la matriz hessiana:
Resolver la matriz hessiana tal como se resuelve la determinante de una matriz cuadrada:
H(x,y,z) = -6
Sacar conclusiones de la respuesta obtenida:
La determinante de la matriz hessiana H(x) o de 1x1 da como resultado – 2 (resultado negativo).
La determinante de la matriz hessiana H(x,y) o de 2x2 da como resultado 3 (resultado positivo).
La determinante de la matriz hessiana H(x,y,z) o de 3x3 da como resultado -6 (resultado negativo).
Anteriormente se explicó que "Si los determinantes tienen signo alterno (comenzando con un valor negativo), entonces la función tiene un MÁXIMO en el punto crítico." Tal como se acaba de ver, los signos se alternan porque tenemos -2, +3 y -6, lo cual significa que la función la función tiene un MÁXIMO en el punto crítico.
Conclusión de la resolución del ejercicio:
La función f(x,y,z) = x² + y² + 7z² - xy es o tiene un máximo en el punto crítico (1/3,2/3,0).
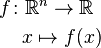

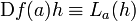
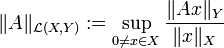
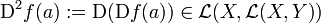
No hay comentarios:
Publicar un comentario