intervalo unidad es el intervalo cerrado [0,1], es decir, el conjunto de todos los números reales que son mayores o iguales que 0 y menores o iguales que 1. A menudo se le denota I. Tiene aplicaciones en análisis de variable realy en el estudio de la teoría de la homotopía en el campo de la topología.
A veces se denota en la literatura por "intervalo unidad" cualquiera de las demás formas que puede tomar un intervalo comprendido entre 0 y 1: (0,1], [0,1) y (0,1). Sin embargo, la notación I se suele reservar al intervalo cerrado [0,1].
Propiedades
El intervalo unidad es un espacio métrico completo, homeomorfo a la recta real extendida. Como espacio topológico, escompacto, contraíble, conexo por caminos y localmente conexo por caminos. El cubo de Hilbert se obtiene tomando un producto topológico de una cantidad numerable de copias del intervalo unidad.
En análisis matemático, el intervalo unidad es una variedad analítica unidimensional cuya frontera consiste en los dos puntos 0 y 1. Su orientación estándar es la que va de 0 a 1.
El conjunto unidad es un conjunto totalmente ordenado y un retículo completo (cada subconjunto del intervalo unidad tienesupremo e ínfimo).
Generalizaciones
A veces se emplea el término de "intervalo unidad" para referirse a objetos que desempeñan un papel en diversas ramas de las matemáticas de forma análoga al que desempeña el intervalo [0,1] en la teoría de la homotopía. Por ejemplo, en la teoría de los grafos orientados, el (análogo del) intervalo unidad es el grafo cuyo conjunto de vértices es {0,1} y que contiene una única arista a cuyo origen es 0 y cuyo destino es 1. Se puede entonces definir una noción de homotopía entre loshomomorfismos de grafos orientados análoga a la existente entre las funciones continuas.
En un sistema de coordenadas cartesianasse han representado las curvas de algunasraíces, así como de sus potencias, en elintervalo unitario. La diagonal, de ecuación y = x, es eje de simetría entre cada curva y la curva de su inversa.
lema de Gronwall establece una cota superior para las funciones no negativas que puedan acotarse por una función lineal de su integral. Este lema es de gran utilidad para probar la continuidad y unicidad de soluciones de ecuaciones diferenciales ordinarias.
Enunciado y demostración
Sean  y
y  tales que:
tales que:
 y
y  tales que:
tales que: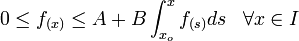 .
.
con A y B ≥ 0 constantes.
Entonces:

Demostración
Sea  . Por la hipótesis se tiene que:
. Por la hipótesis se tiene que:
 . Por la hipótesis se tiene que:
. Por la hipótesis se tiene que: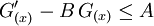
Luego, multiplicando ambos miembros por
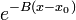 se obtiene:
se obtiene: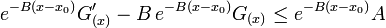
que equivale a:
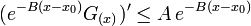
Integrando entre
 y
y  :
: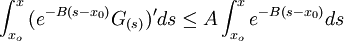

Por como fue definida,
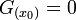 . Multiplicando ahora por
. Multiplicando ahora por  :
: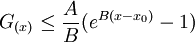
Si reemplazamos la integral por G en la ecuación original:

De donde se deduce que:

Leyes de Plateau describen la estructura de las burbujas de jabón en las espumas. Estas normas fueron formuladas en el Siglo XIX por el físico belga Joseph Plateau de sus observaciones experimentales.
Las Leyes de Plateau describen la forma y configuración de películas de jabón como sigue:
- Las películas de jabón están formadas por superficies suaves (sin arrugas ni bultos) continuas (sin separaciones).
- La curvatura media de una porción de una película de jabón es siempre constante en cualquier punto de la misma porción de la película de jabón.
- Tres películas de jabón se intersecan a lo largo de una línea, formando un ángulo de cos−1(−1/2) = 120 grados, llamada Frontera de Plateau.
- Cuatro de estas Frenteras de Plateau (todas formadas por la intersección de tres superficies) intersecan en un punto, formando un ángulo de cos−1(−1/3) ≈ 109.47 grados (ángulo tetraédrico).
Las configuraciones distintas de las leyes de Plateau son inestables y la espuma rápidamente tienden a reordenarse para que se ajusten a estas normas.
El hecho de que estas leyes se cumplen para superficies mínimas, fue matemáticamente probado utilizando teoría geométrica de la medida por Jean Taylor1
Las leyes enunciadas por Plateau
- Primera ley: "Tres superficies de jabón se intersecan a lo largo de una línea. El ángulo formado por los planos tangenciales a dos superficies que se intersecan, en cualquier punto a lo largo de la línea de intersección de las tres superficies, es de 120 grados".
- Segunda ley: "Cuatro de las líneas, todas formadas por la intersección de tres superficies, se intersecan en un punto y el ángulo formado por cada par de ellas es de 109 grados y 28 minutos ".
- Tercera ley: "Una película de jabón que puede moverse libremente sobre una superficie se interseca con ella formando un ángulo de 90 grados".
límite es una noción topológica que formaliza la noción intuitiva de aproximación hacia un punto concreto de una sucesión o unafunción, a medida que los parámetros de esa sucesión o función se acercan a determinado valor.
En cálculo infinitesimal (especialmente en análisis real y matemático) este concepto se utiliza para definir los conceptos fundamentales de convergencia, continuidad,derivación, integración, entre otros. Si bien, el concepto de límite parece intuitivamente relacionado con el concepto de distancia, en un espacio euclídeo, es la clase deconjuntos abiertos inducidos por dicha métrica, lo que permite definir rigurosamente la noción de límite.
El concepto se puede generalizar a otros espacios topológicos, como pueden ser las redes topológicas; de la misma manera, es definido y utilizado en otras ramas de la matemática, como puede ser la teoría de categorías.
Para fórmulas, el límite se utiliza usualmente de forma abreviada mediante lim como en lim(an) = a o se representa mediante la flecha (→) como en an → a.
Límite de una sucesión
La definición de límite matemático para el caso de una sucesión nos indica intuitivamente que los términos de la sucesión se aproximan arbitrariamente a un único número o punto  , si existe, para valores grandes de
, si existe, para valores grandes de  . Esta definición es muy parecida a la definición del límite de una función cuando
. Esta definición es muy parecida a la definición del límite de una función cuando  tiende a
tiende a  .
.
 , si existe, para valores grandes de
, si existe, para valores grandes de  . Esta definición es muy parecida a la definición del límite de una función cuando
. Esta definición es muy parecida a la definición del límite de una función cuando  tiende a
tiende a  .
.
Formalmente, se dice que la sucesión  tiende hasta su límite
tiende hasta su límite  , o que converge o es convergente (a
, o que converge o es convergente (a  ), y se denota como:
), y se denota como:
 tiende hasta su límite
tiende hasta su límite  , o que converge o es convergente (a
, o que converge o es convergente (a  ), y se denota como:
), y se denota como:
si y solo si para todo valor real ε>0 se puede encontrar un número natural  tal que todos los términos de la sucesión, a partir de un cierto valor natural
tal que todos los términos de la sucesión, a partir de un cierto valor natural  mayor que
mayor que  converjan a
converjan a  cuando
cuando  crezca sin cota. Escrito en un lenguaje formal, y de manera compacta:
crezca sin cota. Escrito en un lenguaje formal, y de manera compacta:
 tal que todos los términos de la sucesión, a partir de un cierto valor natural
tal que todos los términos de la sucesión, a partir de un cierto valor natural  mayor que
mayor que  converjan a
converjan a  cuando
cuando  crezca sin cota. Escrito en un lenguaje formal, y de manera compacta:
crezca sin cota. Escrito en un lenguaje formal, y de manera compacta:
Este límite, si existe, se puede demostrar que es único. Si los términos de la sucesión no convergen a ningún punto específico, entonces se dice que la sucesión esdivergente.
Límite de una función
En análisis real para funciones de una variable, se puede hacer una definición de límite similar a la de límite de una sucesión, en la cual, los valores que toma la función dentro de un intervalo o radio de convergencia se van aproximando a un punto fijado c, independientemente de que éste pertenezca al dominio de la función. El punto c es punto de acumulación del dominio de la función.1 Esto se puede generalizar aún más a funciones de varias variables o funciones en distintosespacios métricos.
Informalmente, se dice que el límite de la función f(x) es L cuando x tiende a c, y se escribe:
si se puede encontrar para cada ocasión un x suficientemente cerca de c tal que el valor de f(x) sea tan próximo a L como se desee.
Para un mayor rigor matemático se utiliza la definición épsilon-delta de límite, que es más estricta y convierte al límite en una gran herramienta del análisis real. Su definición es la siguiente:
"El límite de f(x) cuando x tiende a c es igual a L si y sólo si para todo número real ε mayor que cero existe un número real δ mayor que cero tal que si la distancia entre x y c es menor que δ, entonces la distancia entre la imagen de x y L es menor que ε unidades".
Esta definición, se puede escribir utilizando términos lógico-matemáticos y de manera compacta:
Esta definición es equivalente al límite de una sucesión, una función es continua si:
- Para la función f(x) = x2 - 9/ x - 3 se tiene límite en el punto 3, que no está en el dominio, cuando los valores del dominio se acercan a 3, los valores de la función se aproximan a 6. 3 es un punto de acumulación de Df2
Importancia
El concepto de límite es importante en análisis matemático; una herramienta básica para definir la derivada e integral definida, la existencia de número real al definir por un sistema de intervalos encajados, la potencia real de un real positivo. El plurimilenario caso de π, genial creatura de Arquímedes.3
Límites laterales
Además del límite ordinario en el sentido anterior es posible definir para funciones de una variable los límites unilaterales por la derecha y por la izquierda. El límite por la derecha (cuando existe) es el límite de la sucesión:
Análogamente el límite por la izquierda (cuando existe) es:
para una función continua en c se tiene que 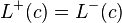 .
.
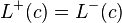 .
.- P
Límite de una sucesión de conjuntos
En teoría de conjuntos también se utiliza el concepto de límite, que se puede calcular sobre una sucesión de conjuntos. Para ello, los conjuntos deben de cumplir una serie de condiciones, como puede ser la monotonía (creciente o decreciente). De manera más general, y utilizando la definición de límite superior y límite inferior para una sucesión de conjuntos cualquiera 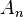 , se dice que el límite de esta sucesión existe si el límite superior y límite inferior existen y son iguales. En general se tiene:
, se dice que el límite de esta sucesión existe si el límite superior y límite inferior existen y son iguales. En general se tiene:
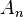 , se dice que el límite de esta sucesión existe si el límite superior y límite inferior existen y son iguales. En general se tiene:
, se dice que el límite de esta sucesión existe si el límite superior y límite inferior existen y son iguales. En general se tiene:
Si el límite primer término y el penúltimo son iguales entonces se verifican todas las igualdades. Estos conceptos son muy útiles en disciplinas de las matemáticas como la teoría de la medida, especialmente en espacios de probabilidad. No es difícil construir sucesiones no convergentes donde se verifica que:
Límite en espacios topológicos
Redes
Véase también: Red (matemáticas)
Todas las nociones anteriores de límite pueden ser unificadas y generalizadas a espacios topológicos arbitrarios mediante la introducción de redes topológicas y la definición de sus límites.
Sea  un espacio topológico y
un espacio topológico y 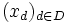 una red en
una red en  . Se dice que
. Se dice que  es un punto límite de la red
es un punto límite de la red 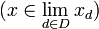 si la red está eventualmente en cadaentorno de
si la red está eventualmente en cadaentorno de  , es decir, si cualquiera que sea el entorno
, es decir, si cualquiera que sea el entorno  de
de  (esto es, cualquiera que sea el conjunto
(esto es, cualquiera que sea el conjunto  de forma que exista un abierto
de forma que exista un abierto  tal que
tal que  ) existe un
) existe un  de tal forma que para cada
de tal forma que para cada 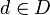 con
con  se cumple que
se cumple que 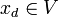 .
.
 un espacio topológico y
un espacio topológico y 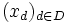 una red en
una red en  . Se dice que
. Se dice que  es un punto límite de la red
es un punto límite de la red 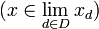 si la red está eventualmente en cadaentorno de
si la red está eventualmente en cadaentorno de  , es decir, si cualquiera que sea el entorno
, es decir, si cualquiera que sea el entorno  de
de  (esto es, cualquiera que sea el conjunto
(esto es, cualquiera que sea el conjunto  de forma que exista un abierto
de forma que exista un abierto  tal que
tal que  ) existe un
) existe un  de tal forma que para cada
de tal forma que para cada 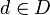 con
con  se cumple que
se cumple que 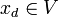 .
.Filtros
Véase también: Filtro (matemáticas)
En el caso de filtros, por ser objetos matemáticos similares a redes topológicas, también es posible la definición de límite. En efecto, sea X un espacio topológico y x un punto de X. Se dice que un filtro base B converge a x, denotado como B → x o 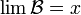 , si para todo entorno U de x, existe un B0 ∈ B tal que B0 ⊆ U. En este caso,x se llama límite de B y B se denomina filtro base convergente.4 5
, si para todo entorno U de x, existe un B0 ∈ B tal que B0 ⊆ U. En este caso,x se llama límite de B y B se denomina filtro base convergente.4 5
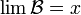 , si para todo entorno U de x, existe un B0 ∈ B tal que B0 ⊆ U. En este caso,x se llama límite de B y B se denomina filtro base convergente.4 5
, si para todo entorno U de x, existe un B0 ∈ B tal que B0 ⊆ U. En este caso,x se llama límite de B y B se denomina filtro base convergente.4 5
De igual manera, se puede aplicar a funciones, extendiendo la definición de continuidad a éstas. Si X, Y son dos espacios topológicos y f: X → Y es una función, siendoB un filtro entorno en X de un punto a perteneciente a X, entonces el límite con respecto al filtro B de f es y, denotado como
si B converge a a, luego f converge a y; dicho de otra forma, y es el límite de f en el punto a.4
Límite de Banach
En análisis funcional, un límite de Banach es un funcional lineal continuo  definido sobre el espacio de Banach
definido sobre el espacio de Banach  para toda sucesión acotada denúmeros complejos, donde se cumplen una serie de condiciones entre las que se encuentra que si
para toda sucesión acotada denúmeros complejos, donde se cumplen una serie de condiciones entre las que se encuentra que si  es una sucesión convergente, entonces
es una sucesión convergente, entonces  , generalizando el concepto de límite. Por lo tanto,
, generalizando el concepto de límite. Por lo tanto,  es una extensión del funcional continuo
es una extensión del funcional continuo  6
6
 definido sobre el espacio de Banach
definido sobre el espacio de Banach  para toda sucesión acotada denúmeros complejos, donde se cumplen una serie de condiciones entre las que se encuentra que si
para toda sucesión acotada denúmeros complejos, donde se cumplen una serie de condiciones entre las que se encuentra que si  es una sucesión convergente, entonces
es una sucesión convergente, entonces  , generalizando el concepto de límite. Por lo tanto,
, generalizando el concepto de límite. Por lo tanto,  es una extensión del funcional continuo
es una extensión del funcional continuo  6
6
En particular, la existencia del límite de Banach no es única.6
Límites en teoría de categorías
En teoría de categorías, una rama de la matemática, se define el concepto abstracto de límite, el cual usa propiedades esenciales de construcciones universales tales como productos y límites inversos.


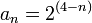 para
para  converge al valor 0, como se puede ver en la ilustración.
converge al valor 0, como se puede ver en la ilustración.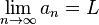

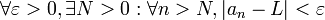


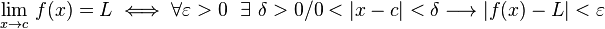

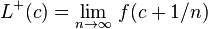


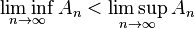
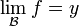
No hay comentarios:
Publicar un comentario