punto anguloso (aislado) de una función es un punto donde la función es continua pero la derivada en un entorno de dicho punto es discontinua (más exactamente tiene una discontinuidad no evitable de primera especie).
Los puntos angulosos son los únicos puntos en donde una función es continua, pero no puede trazarse una recta tangente a la función en dicho punto.
Esto se debe a que una función es continua en un punto, implica que las derivadas laterales en dicho punto determinan un ángulo llano entre ellas (180º) y las rectas normales a cada derivada lateral son coincidentes entre si, (forman un ángulo de 0º).
En un punto anguloso aislado, esto no se cumple, las derivadas laterales forman un ángulo no llano lo que le da el nombre a este tipo de punto. Además, como consecuencia, no existe la normal en este punto. Además existen funciones tales que todos sus puntos son angulosos, o más exactamente donde no existe la derivada en ningún punto a pesar de que su grafo es una curva continua, uno de los primeros ejemplos de este tipo de funciones lo constituyó la función de Weierstrass:
siendo los números reales a y b tales que:

- punto crítico de una función de una variable real es cualquier valor en el dominio en donde la función no es diferenciable o cuando su derivada es 0.1 2 El valor de la función en el punto crítico es un valor crítico de la función. Estas definiciones admiten generalizaciones a funciones de varias variables, mapas diferenciables entre Rm y Rn, y mapas diferenciables entre variedades diferenciables.
Definición para funciones de una sola variable
Un punto crítico de una función de una sola variable real, ƒ(x), es un valor x0 dentro del dominio de ƒ donde la función no es diferenciable, o bien, su derivada es 0, ƒ′(x0) = 0. Cualquier valor en el codominio de ƒ que sea la imagen de un punto crítico bajo ƒ es un valor crítico de ƒ. Estos conceptos pueden ser visualizados por medio de la gráfica de ƒ: en un punto crítico, la gráfica no admite una tangente, o bien, la tangente es una línea vertical u horizontal. En el último caso, la derivada es cero y el punto es llamado un punto estacionario de la función.Optimización
Por el teorema de Fermat, los máximos y mínimos locales de una función pueden ocurrir únicamente en sus puntos críticos. Sin embargo, no todo punto estacionario es un máximo o mínimo de la función; puede corresponder también a un punto de inflexión de la gráfica, como para ƒ(x) = x3 en x = 0, o la gráfica puede oscilar en la vecindad del punto, como en el caso de la función definida por la fórmula ƒ(x) = x2sen(1/x) para x ≠ 0 y ƒ(0) = 0, en el punto x = 0.Ejemplos
- La función ƒ(x) = x2 + 2x + 3 es diferenciable en todo lugar, con la derivada ƒ′(x) = 2x + 2. Esta función tiene un único punto crítico −1, debido a que es el único número x0 para el cual 2x0 + 2 = 0. Este punto es un mínimo global de ƒ. El correspondiente valor crítico es ƒ(−1) = 2. La gráfica de ƒ es una parábola cóncava hacia arriba, el punto crítico es la abscisa del vértice, donde la línea tangente es horizontal, y el valor crítico es la ordenada del vértice y puede ser representado por la intersección de esta línea tangente y el eje y.
- La función f(x) = x2/3 está definida para toda x y es diferenciable para x ≠ 0, con la derivada ƒ′(x) = 2x−1/3/3. Debido a que ƒ′(x) ≠ 0 para x ≠ 0, el único punto crítico de ƒ es x = 0. La gráfica de la función ƒ tiene una cúspide en este punto con una tangente vertical. El correspondiente valor crítico es ƒ(0) = 0.
- La función ƒ(x) = x3 − 3x + 1 es diferenciable en todas partes, con la derivada ƒ′(x) = 3x2 − 3. Tiene dos puntos críticos, en x = −1 y x = 1. Los correspondientes valores críticos son ƒ(−1) = 3, que es un valor máximo local, y ƒ(1) = −1, que es un valor mínimo local de ƒ. Esta función no tiene máximo o mínimo global. Debido a que ƒ(2) = 3, se observa que un valor crítico puede también ser alcanzado en un punto no crítico. Geométricamente, esto significa que una línea tangente horizontal a la gráfica en un punto (x = −1) puede intersecar la gráfica en un ángulo agudo en otro punto (x = 2).
- La función
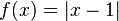 es derivable en todo su domínio excepto en
es derivable en todo su domínio excepto en 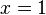 , luego el
, luego el  es el único punto crítico; a pesar de que existen las derivadas laterales en tal punto, pero distintas. 3
es el único punto crítico; a pesar de que existen las derivadas laterales en tal punto, pero distintas. 3
- La función máximo entero de x, conocida como tal en análisis matemático y teoría de números
no es derivable para valores enteros de x; por lo tanto tiene una infinidad numerable de puntos críticos. 4Funciones de varias variables
En esta sección, se asumirá que las funciones son suaves.Para una función suave de varias variables reales, la condición de ser un punto crítico es equivalente a que todas sus derivadas parciales sean cero; para una función en una variedad, es equivalente a que su diferencial sea cero.Si la matriz hessiana en un punto crítico es no singular entonces el punto crítico es llamado no degenerado, y el signo de los autovalores del Hessiano determinan el comportamiento local de la función. En el caso de una función real de una variable real, el Hessiano es simplemente la segunda derivada, y la no singularidad es equivalente a ser diferente de cero. Un punto crítico no degenerado de una función real de una variable es un máximo si la segunda derivada es negativa, y un mínimo si es positiva. Para una función de n variables, el número de autovalores negativos de un punto crítico es llamado su índice, y un máximo ocurre cuando todos los autovalores son negativos (índice n, la matriz hessiana es definida negativa) y un mínimo ocurre cuando todos los autovalores son positivos (índice cero, la matriz hessiana es definida positiva); en todos los otros casos, el punto crítico puede ser un máximo, un mínimo o un punto de silla (índice estrictamente entre 0 y n, la matriz hessiana es indefinida). La Teoría de Morse aplica estas ideas a la determinación de la topología de variedades, tanto de dimensión finita o infinita.Campo vectorial gradiente
En la presencia de una métrica Riemanniana o una forma simpléctica, a cada función suave le es asociada un campo vectorial (el gradiente o campo vectorial Hamiltoniano). Estos campos vectoriales desaparecen exactamente en los puntos críticos de la función original, y así los puntos críticos son estacionarios, es decir, las trayectorias constantes del flujo asociado al campo vectorial.Definición para mapas5
Para un mapa diferenciable f entre Rm y Rn, los puntos críticos son los puntos donde el diferencial de f es una aplicación lineal de rango menor que n; en particular, cada punto es crítico si m < n. Esta definición inmediatamente se extiende a mapas entre variedades suaves. La imagen de un punto bajo f es llamada un valor crítico. Un punto en el complemento del conjunto de valores críticos es llamado un valor regular. El teorema de Sard dice que el conjunto de valores críticos de un mapa suave tiene medida cero.- punto de acumulación (también denominado de contacto o límite o punto de aglomeración 1 ) de un conjunto en un espacio captura la noción informal de punto que está arbitrariamente próximo al conjunto sin pertenecer necesariamente a él. Informalmente hablando, un punto de acumulación de un conjunto S en un espacio topológico X es un punto x en X que puede ser aproximado por puntos de S distintos a x tanto como se desee.Este concepto generaliza la noción de límite y puede ser base de conceptos como conjunto cerrado y cerradura topológica. Ciertamente, un conjunto es cerrado si y solo si contiene todos sus puntos de acumulación, y la operación topológica de cerradura puede considerarse como el resultado de agregar a un conjunto todos sus puntos de acumulación.
Definición
Si S es un subconjunto de un espacio topológico X, un punto es un punto de acumulación de S si cualquier conjunto abierto que contenga a x contiene otro punto
es un punto de acumulación de S si cualquier conjunto abierto que contenga a x contiene otro punto  distinto de x. Es decir, cualquier vecindad de x contiene un punto de S distinto a x.
distinto de x. Es decir, cualquier vecindad de x contiene un punto de S distinto a x.- Ejemplos
- El intervalo
 tiene como puntos de acumulación a todos los puntos del intervalo
tiene como puntos de acumulación a todos los puntos del intervalo ![[0,1]](https://upload.wikimedia.org/math/c/c/f/ccfcd347d0bf65dc77afe01a3306a96b.png) .
.
- Un conjunto finito de números reales en la topología estándar no tiene puntos de acumulación.
- Sin embargo, cualquier número es un punto de acumulación de un conjunto finito en la topología indiscreta de los números reales.
 no tiene puntos de acumulación cuando se considera como subconjunto de
no tiene puntos de acumulación cuando se considera como subconjunto de  en la topología estándar. Por lo tanto, cada punto en
en la topología estándar. Por lo tanto, cada punto en  es aislado.
es aislado.
Propiedades
Caracterización de los puntos de acumulación
x es un punto límite de S si y solo sí está en la cerradura de S \ {x}. 'Demostración: Partamos del hecho de que un punto está en la cerradura de un conjunto si y solo si toda vecindad del punto tiene intersección no vacía con el conjunto. Ahora, x es un punto límite de S ssi toda vecindad de x contiene un punto de S distinto a x ssi toda vecindad de x contiene un punto de S \ {x} sii x está en la cerradura de S \ {x}.- Si usamos L(S) para denotar el conjunto de puntos límite de S, entonces tenemos la siguiente caracterización de la cerradura de S: La cerradura de S es igual a la unión de S y L(S).
- Demostración: Supongamos que x está en la cerradura de S. Si x está en S, está demostrado. Si x no está en S, entonces toda vecindad de x contiene un punto de S, y este punto no puede ser s. En otras palabras, x es un punto límite de S y x está en L(S).
Recíprocamente, si x está en S, entonces toda vecindad de x claramente tiene intersección no vacía con S, así que x está en la cerradura de S. Si x está en L(S), entonces toda vecindad de x contiene un punto de S (distinto de x), así que x está en la cerradura de S. Esto completa la prueba.- Un corolario de este resultado nos da una caracterización de los conjuntos cerrado: un conjunto S es cerrado si y solo si este contiene a todos sus puntos límite.
Caracterización de conjuntos cerrados
- Teorema:
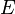 es un conjunto cerrado si
es un conjunto cerrado si 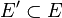 , donde
, donde 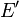 es el conjunto de todos los puntos de acumulación de
es el conjunto de todos los puntos de acumulación de 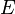 .
.
Válido en espacios métricos y topológicos. Y válido en cualquier espacio.Otras propiedades
- Ningún punto aislado es el punto de límite de un conjunto que no lo contenga.
- Un espacio X es discreto si y solo si ningún subconjunto de X tiene puntos límites.
- Si un espacio X tiene la topología trivial y S es un subconjunto de X con más de un elemento, entonces todos los elementos de X son puntos límites de S.
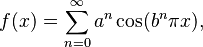
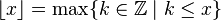
No hay comentarios:
Publicar un comentario