radio de una circunferencia es cualquier segmento que une el centro a cualquier punto de dicha circunferencia.
La longitud del radio es la mitad de la del diámetro. Todos los radios de una figura geométrica poseen la misma longitud.
El radio de una esfera: cualquier segmento que une el centro con un punto de su superficie esférica.
El radio de un poliedro regular: no es sino el radio de la esfera circunscrita1
Se llama radio de un polígono regular al radio de la circunferencia circunscrita (es el segmento que une su centro con cualquiervértice). El radio de la circunferencia inscrita se llama apotema del polígono.
Radio de curvatura: es la magnitud R, recíproca a la curvatuta K de una curva en un punto dado M, se denomina radio de curvatura de la curva en este punto de que se trata.2
En un sentido más general —en geometría, ingeniería, teoría de grafos y muchos otros contextos—, el radio (por ejemplo, de uncilindro, un polígono, un grafo o una parte mecánica) es el segmento que une su centro (o eje) y sus puntos más externos.
- Radio de torsión. La magnitud que caracteriza la desviación de la curva en el espacio respecto de la curva plana. La magnitud T se llama radio de torsión3
- Radio de una vecindad. Si la vecindad es el intervalo abierto (a;b), entonces el radio es [a + b]/2.
- Radio vector: es el segmento, en una hipérbola o elipse, que une los focos con un punto de la misma4
- Radio de convergencia de una serie. Partiendo de una serie formal, que tiene coeficientes en el conjunto de los números reales o de los complejos, se define al número real R > 0 tal que la serie converge absolutamente para |z| < R y diverge si |z| > R2
- Radio de giro . El radio de giro K de un sólido respecto de un eje de giro e viene a ser la distancia al eje e a la que debería situarse una partícula cuya masa fuera igual a la masa total del sólido para que dicha partícula tuviera el mismo momento de inercia que el cuerpo.
recta real extendida o recta real acabada, es un espacio métrico que se obtiene a partir de los números reales  por la añadidura de dos elementos:
por la añadidura de dos elementos: y
y  (léase infinito positivo e infinito negativo, respectivamente). La recta real extendida proyectiva añade un solo objeto:
(léase infinito positivo e infinito negativo, respectivamente). La recta real extendida proyectiva añade un solo objeto:  (punto del infinito), y no hace distinción entre infinitos «positivo» o «negativo». Estos nuevos elementos no son números reales.
(punto del infinito), y no hace distinción entre infinitos «positivo» o «negativo». Estos nuevos elementos no son números reales.
 por la añadidura de dos elementos:
por la añadidura de dos elementos: y
y  (léase infinito positivo e infinito negativo, respectivamente). La recta real extendida proyectiva añade un solo objeto:
(léase infinito positivo e infinito negativo, respectivamente). La recta real extendida proyectiva añade un solo objeto:  (punto del infinito), y no hace distinción entre infinitos «positivo» o «negativo». Estos nuevos elementos no son números reales.
(punto del infinito), y no hace distinción entre infinitos «positivo» o «negativo». Estos nuevos elementos no son números reales.
La recta real extendida se denota por 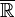 o bien
o bien ![[+ \infty,- \infty]](https://upload.wikimedia.org/math/0/4/8/048d7efbc9b806ef73a3d1119a89efda.png) ; es utilizada para describir varios comportamientos al límite en cálculo infinitesimal y análisis matemático, especialmente en la teoría de la medida e integración.
; es utilizada para describir varios comportamientos al límite en cálculo infinitesimal y análisis matemático, especialmente en la teoría de la medida e integración.
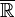 o bien
o bien ![[+ \infty,- \infty]](https://upload.wikimedia.org/math/0/4/8/048d7efbc9b806ef73a3d1119a89efda.png) ; es utilizada para describir varios comportamientos al límite en cálculo infinitesimal y análisis matemático, especialmente en la teoría de la medida e integración.
; es utilizada para describir varios comportamientos al límite en cálculo infinitesimal y análisis matemático, especialmente en la teoría de la medida e integración.
Cuando el significado se deduce del contexto, el símbolo  se escribe simplemente
se escribe simplemente  .
.
 se escribe simplemente
se escribe simplemente  .
.Definiciones
Límites
La necesidad de su definición, surge al describir el comportamiento de una función f(x), cuando o bien el argumento x o bien el valor de la función f(x) se vuelve «muy grande» en algún sentido.
Por ejemplo, la función 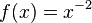 .
.
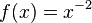 .
.
La gráfica de esta función tiene una asíntota horizontal en f(x) = 0. Geométricamente, esto significa que conforme el valor de x crece (hacia la derecha del plano cartesiano), más se aproxima el valor de 1/x2 a 0 (el eje horizontal). Este comportamiento al límite es similar al del límite de una función en un número real, excepto que ahí no hay número real hacia el cual x se aproxima.
Añadiéndole los elementos +∞ y −∞ a R, se permite la formulación de "límite al infinito" con propiedades topológicas similares a las de R.
Medida e integración
En teoría de la medida, se suelen admitir conjuntos que tienen medida infinita e integrales cuyo valor puede ser infinito.
Tales medidas surgen naturamente del cálculo. Por ejemplo, si se le asigna una medida a R correspondiente con la longitud usual de los intervalos, esta medida debe ser mayor que cualquier número real finito. También, si se consideran integrales no acotadas, como
surge el valor "infinito". Finalmente, se suele considerar el límite de una sucesión de funciones, como
Si no permitiesen valores infinitos a funciones, resultados tan esenciales como el teorema de convergencia monótona y el teorema de convergencia dominada no tendrían sentido.
Orden y propiedades topológicas
La recta real extendida se vuelve un conjunto totalmente ordenado definiendo −∞ ≤ a ≤ +∞ para todo a. Este orden tiene la agradable propiedad de que todo subconjunto tiene un supremo y un ínfimo: conforma un retículo completo.
Esto induce un orden topológico sobre R. En esta topología, un conjunto U es una vecindad de +∞ si y solo si contiene un conjunto {x: x > a} para algún número real a, y análogamente para las vecindades de −∞. R es un espacio de Hausdorff compacto homeomorfo al intervalo unidad [0, 1]. Luego esta topología es metrizable, corresponde (para un homeomorfismo dado) a la métrica usual en este intervalo. No hay una métrica que sea una extensión de la métrica usual sobre R.
Con esta topología, se pueden definir especialmente los límites para x tendiendo a +∞ y −∞, y los conceptos especialmente definidos de límites igual a +∞ y −∞, se reducen a la definición topológica de límites.
Propiedades aritméticas
Las propiedades aritméticas de R pueden extenderse parcialmente a R del siguiente modo:
Aquí, "a + ∞" significan ambos "a + (+∞)" y "a − (−∞)", y "a − ∞" significan ambos "a − (+∞)" y "a + (−∞)".
Las expresiones ∞ − ∞, 0 × (±∞) y ±∞ / ±∞ (llamadas formas indeterminadas) son usualmente indefinidas a la izquierda. Son reglas modeladas por las leyes de loslímites infinitos. No obstante, en el contexto de la probabilidad o teoría de la medida, 0 × (±∞) se define a menudo como 0.
La expresión 1/0 no se define ni como +∞ ni como −∞, porque aunque es cierto que cuando f(x) → 0 para una función continua f(x) debe suceder que 1/f(x) está eventualmente contenida en toda vecindad del conjunto {−∞, +∞}, no es cierto que 1/f(x) deben tender a uno de estos puntos. Un ejemplo es f(x) = sin(x)/x. Esto deja de suceder al aplicar el valor absoluto a la función, quedando 1/| f(x) |, en ese caso se aproxima a +∞.
Propiedades algebraicas
Con las definiciones arriba expuestas, R no es un cuerpo ni un anillo, pero posee las siguientes propiedades:
- a + (b + c) y (a + b) + c son ambos o bien iguales o bien indefinidos.
- a + b yb + a son ambos o bien iguales o bien indefinidos.
- a × (b × c) y (a × b) × c son ambos o bien iguales o bien indefinidos.
- a × b yb × a son ambos o bien iguales o bien indefinidos.
- a × (b + c) y (a × b) + (a × c) son ambos o bien iguales o bien indefinidos.
- if a ≤ b y si ambos a + c yb + c están definidos, entonces a + c ≤ b + c.
- if a ≤ b yc > 0 y ambos a × c y b × c están definidos, entonces a × c ≤ b × c.
En general, todas las leyes de la aritmética serán válidas en R siempre y cuando las expresiones que intervienen estén definidas.
red es la generalización del concepto de sucesión, de tal manera que no necesariamente tenga una cantidad numerable de elementos. Es el concepto más adecuado (o también su equivalente de filtro) para estudiar la convergencia en un espacio topológico.
Definición
Conjunto dirigido
Un conjunto dirigido es un par  en el que
en el que  es un conjunto y
es un conjunto y 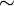 es una relación en
es una relación en  que verifica las siguientes propiedades:
que verifica las siguientes propiedades:
 en el que
en el que  es un conjunto y
es un conjunto y 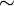 es una relación en
es una relación en  que verifica las siguientes propiedades:
que verifica las siguientes propiedades: (propiedad reflexiva).
(propiedad reflexiva). tales que
tales que 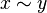 e
e 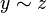 , se cumple entonces que
, se cumple entonces que 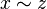 (propiedad transitiva).
(propiedad transitiva). tal que
tal que 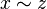 e
e 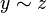 .
.
Usualmente, la relación 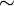 se lee como "menor igual" (en forma intuitiva).
se lee como "menor igual" (en forma intuitiva).
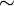 se lee como "menor igual" (en forma intuitiva).
se lee como "menor igual" (en forma intuitiva).
En particular, todo conjunto totalmente ordenado es un conjunto dirigido. Un ejemplo importante de conjunto dirigido es 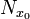 , el conjunto de las vecindades de un punto
, el conjunto de las vecindades de un punto  en un espacio topológico, dotado de la relación de inclusión, donde un conjunto se dirá "mayor" que otro si está incluido en él.
en un espacio topológico, dotado de la relación de inclusión, donde un conjunto se dirá "mayor" que otro si está incluido en él.
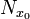 , el conjunto de las vecindades de un punto
, el conjunto de las vecindades de un punto  en un espacio topológico, dotado de la relación de inclusión, donde un conjunto se dirá "mayor" que otro si está incluido en él.
en un espacio topológico, dotado de la relación de inclusión, donde un conjunto se dirá "mayor" que otro si está incluido en él.Red
Una red en un conjunto  no es más que una aplicación
no es más que una aplicación 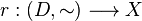 entre un conjunto dirigido
entre un conjunto dirigido  y un conjunto
y un conjunto  . Se suele representar por
. Se suele representar por 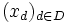 , donde
, donde  .
.
 no es más que una aplicación
no es más que una aplicación 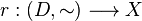 entre un conjunto dirigido
entre un conjunto dirigido  y un conjunto
y un conjunto  . Se suele representar por
. Se suele representar por 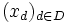 , donde
, donde  .
.Subred
Tal como en el contexto de sucesiones hay una noción de subsucesiones, en el concepto de redes también hay un concepto similar. Así, decimos que  es una subred de
es una subred de 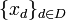 (donde
(donde 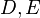 son conjuntos dirigidos) si y solo si existe una función
son conjuntos dirigidos) si y solo si existe una función  que verifica las siguientes dos propiedades:
que verifica las siguientes dos propiedades:
 es una subred de
es una subred de 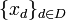 (donde
(donde 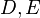 son conjuntos dirigidos) si y solo si existe una función
son conjuntos dirigidos) si y solo si existe una función  que verifica las siguientes dos propiedades:
que verifica las siguientes dos propiedades: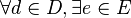 tal que
tal que 

La primera condición refleja la idea intuitiva de que la sub-red se "vaya a infinito" junto con la red, mientras que la segunda es simplemente pedir que los puntos que tome sean efectivamente puntos de la red.
Es fácil ver que toda subred de una red es también una red.
Convergencia
Límite de una red
Sea  un espacio topológico y
un espacio topológico y 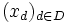 una red en
una red en  . Se dice que
. Se dice que  es un punto límite de la red
es un punto límite de la red 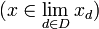 si la red está eventualmente en cadaentorno de
si la red está eventualmente en cadaentorno de  , es decir, si cualquiera que sea el entorno
, es decir, si cualquiera que sea el entorno 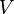 de
de  (esto es, cualquiera que sea el conjunto
(esto es, cualquiera que sea el conjunto 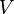 de forma que exista un abierto
de forma que exista un abierto  tal que
tal que  ) existe un
) existe un  de tal forma que para cada
de tal forma que para cada  con
con  se cumple que
se cumple que 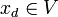 .
.
 un espacio topológico y
un espacio topológico y 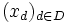 una red en
una red en  . Se dice que
. Se dice que  es un punto límite de la red
es un punto límite de la red 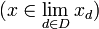 si la red está eventualmente en cadaentorno de
si la red está eventualmente en cadaentorno de  , es decir, si cualquiera que sea el entorno
, es decir, si cualquiera que sea el entorno 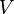 de
de  (esto es, cualquiera que sea el conjunto
(esto es, cualquiera que sea el conjunto 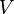 de forma que exista un abierto
de forma que exista un abierto  tal que
tal que  ) existe un
) existe un  de tal forma que para cada
de tal forma que para cada  con
con  se cumple que
se cumple que 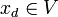 .
.
De la propia definición se desprenden de forma inmediata dos consecuencias:
- El límite de una red no siempre ha de existir. Existen redes que carecen de límite.
- En caso de existir, el límite de una red no necesariamente es un único elemento, sino que es un conjunto de elementos. En el caso de espacios topológicos con lapropiedad de Hausdorff (i.e., T2), el límite, si existe, se reduce a un único punto.
- Toda sub-red de una red convergente converge al mismo límite que la red
Punto de Acumulación
Bajo el mismo contexto anterior, se dice que una red 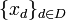 tiene como punto de acumulación (o acumula en)
tiene como punto de acumulación (o acumula en)  si la red está frecuentemente en cada entorno de
si la red está frecuentemente en cada entorno de  , es decir, si para todo
, es decir, si para todo 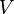 entorno de
entorno de  , y para todo
, y para todo  tal que
tal que  .
.
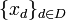 tiene como punto de acumulación (o acumula en)
tiene como punto de acumulación (o acumula en)  si la red está frecuentemente en cada entorno de
si la red está frecuentemente en cada entorno de  , es decir, si para todo
, es decir, si para todo 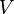 entorno de
entorno de  , y para todo
, y para todo  tal que
tal que  .
.
Es fácil ver que toda red convergente tiene a su límite como punto de acumulación. Se cumple además que  es punto de acumulación de una red si y solamente si existe una sub-red que converge a
es punto de acumulación de una red si y solamente si existe una sub-red que converge a  . En este punto se encuentra la primera gran diferencia con sucesiones: una sucesión (que en particular es una red) tiene a
. En este punto se encuentra la primera gran diferencia con sucesiones: una sucesión (que en particular es una red) tiene a  como punto de acumulación si y solo si existe una sub-red que tienda a
como punto de acumulación si y solo si existe una sub-red que tienda a  , pero esta sub-red no tiene porqué ser una sucesión también.
, pero esta sub-red no tiene porqué ser una sucesión también.
 es punto de acumulación de una red si y solamente si existe una sub-red que converge a
es punto de acumulación de una red si y solamente si existe una sub-red que converge a  . En este punto se encuentra la primera gran diferencia con sucesiones: una sucesión (que en particular es una red) tiene a
. En este punto se encuentra la primera gran diferencia con sucesiones: una sucesión (que en particular es una red) tiene a  como punto de acumulación si y solo si existe una sub-red que tienda a
como punto de acumulación si y solo si existe una sub-red que tienda a  , pero esta sub-red no tiene porqué ser una sucesión también.
, pero esta sub-red no tiene porqué ser una sucesión también.Aplicaciones
Continuidad
Así como en espacios métricos existe una caracterización de la continuidad mediante sucesiones, en espacios topológicos generales esta caracterización se hace mediante redes. Así, se cumple que si  son dos espacios topológicos,
son dos espacios topológicos, 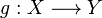 será continua en el punto
será continua en el punto 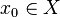 si y solamente si para toda red
si y solamente si para toda red  , se cumple que
, se cumple que 
 son dos espacios topológicos,
son dos espacios topológicos, 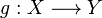 será continua en el punto
será continua en el punto 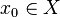 si y solamente si para toda red
si y solamente si para toda red  , se cumple que
, se cumple que 
Compacidad
Así como en espacios métricos se tiene que  es compacto si y solo si toda sucesión tiene un punto de acumulación, en espacios más generales se tiene el mismo resultado, pero con redes, es decir,
es compacto si y solo si toda sucesión tiene un punto de acumulación, en espacios más generales se tiene el mismo resultado, pero con redes, es decir,  será compacto si y solo si toda red tiene un punto de acumulación.
será compacto si y solo si toda red tiene un punto de acumulación.
 es compacto si y solo si toda sucesión tiene un punto de acumulación, en espacios más generales se tiene el mismo resultado, pero con redes, es decir,
es compacto si y solo si toda sucesión tiene un punto de acumulación, en espacios más generales se tiene el mismo resultado, pero con redes, es decir,  será compacto si y solo si toda red tiene un punto de acumulación.
será compacto si y solo si toda red tiene un punto de acumulación.
Notar que en espacios métricos, casi todo lo que se puede hacer con redes también se puede hacer con sucesiones, y como estas últimas son más fáciles de manipular, usualmente se trabaja con ellas. Sin embargo, en espacios topológicos generales, las redes pueden ser de gran utilidad.
Ejemplos
El ejemplo más inmediato de red es el concepto de sucesión. En ellas, el conjunto dirigido es el conjunto de los números naturales con la relación de orden usual. Esto es así porque el conjunto de los números naturales con el orden usual es un conjunto totalmente ordenado.
Otro ejemplo esencial es el de función de variable real. En efecto, como el conjunto de los números reales junto con el orden usual es un conjunto totalmente ordenado, una función de variable real es una red.
Estos dos ejemplos son lo suficientemente importantes como para justificar el estudio de las redes.

donde 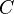 representa una circunferencia de centro
representa una circunferencia de centro  en cuyo interior no hay puntos singulares de la función salvo
en cuyo interior no hay puntos singulares de la función salvo  .
.
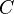 representa una circunferencia de centro
representa una circunferencia de centro  en cuyo interior no hay puntos singulares de la función salvo
en cuyo interior no hay puntos singulares de la función salvo  .
.Cálculo de residuos
Si 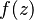 tiene una singularidad evitable en
tiene una singularidad evitable en  , el residuo es
, el residuo es 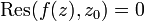 . Si
. Si 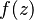 tiene un polo de orden
tiene un polo de orden  en
en  , entonces el residuo se puede calcular como:
, entonces el residuo se puede calcular como:
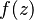 tiene una singularidad evitable en
tiene una singularidad evitable en  , el residuo es
, el residuo es 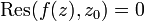 . Si
. Si 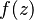 tiene un polo de orden
tiene un polo de orden  en
en  , entonces el residuo se puede calcular como:
, entonces el residuo se puede calcular como:
En particular, si  (polo simple),
(polo simple),
 (polo simple),
(polo simple),
Si el punto  es una singularidad esencial, el residuo se calcula desarrollando la función en serie de Laurent en torno a
es una singularidad esencial, el residuo se calcula desarrollando la función en serie de Laurent en torno a  . El residuo es el coeficiente correspondiente a la potencia de exponente
. El residuo es el coeficiente correspondiente a la potencia de exponente  .
.
 es una singularidad esencial, el residuo se calcula desarrollando la función en serie de Laurent en torno a
es una singularidad esencial, el residuo se calcula desarrollando la función en serie de Laurent en torno a  . El residuo es el coeficiente correspondiente a la potencia de exponente
. El residuo es el coeficiente correspondiente a la potencia de exponente  .
.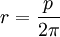 .
.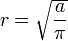 .
.

![\begin{align}
a + \infty = +\infty + a & = +\infty, & a & \neq -\infty \\
a - \infty = -\infty + a & = -\infty, & a & \neq +\infty \\
a \cdot (\pm\infty) = \pm\infty \cdot a & = \pm\infty, & a & \in (0, +\infty] \\
a \cdot (\pm\infty) = \pm\infty \cdot a & = \mp\infty, & a & \in [-\infty, 0) \\
\frac{a}{\pm\infty} & = 0, & a & \in \mathbb{R} \\
\frac{\pm\infty}{a} & = \pm\infty, & a & \in \mathbb{R}^+ \\
\frac{\pm\infty}{a} & = \mp\infty, & a & \in \mathbb{R}^-
\end{align}](https://upload.wikimedia.org/math/2/a/6/2a657e0e14868dec76c3c30404dcbc22.png)
 al número
al número![\operatorname{Res}(f,z_0)= \lim_{z\to z_0} \, \, \frac{1}{(N-1)!} \frac{d^{N-1}}{dz^{N-1}}[(z-z_0)^N f(z)]](https://upload.wikimedia.org/math/b/2/9/b2916d55ea60a422e3533dacb6171aee.png)
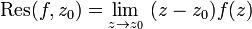
No hay comentarios:
Publicar un comentario