multiplicidad de un miembro de un multiconjunto es el número de pertenencias que éste tiene en el multiconjunto. Por ejemplo, este término se usa para referirse al número de veces que cierto polinomio tiene raíz en un punto determinado.
La razón más habitual para considerar nociones de multiplicidad es para contar sin especificar excepciones (por ejemplo, especificar que las raíces dobles se cuentan dos veces). De aquí la expresión contado con multiplicidad (en ocasiones implícita).
Multiplicidad de un factor primo
En la factorización en factores primos
- 60 = 2 × 2 × 3 × 5
la multiplicidad de 2 es 2; la de 3 es 1, y la de 5 es 1. Así, 60 tiene 3 factores primos, pero sólo 3 factores primos distintos.
Multiplicidad de la raíz de un polinomio
Sea  un campo y
un campo y 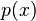 un polinomio de una variable con coeficientes en
un polinomio de una variable con coeficientes en  . Un elemento
. Un elemento  ∈
∈  se llama raíz de multiplicidad
se llama raíz de multiplicidad  de
de 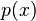 si existe un polinomio
si existe un polinomio  tal que
tal que 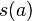 ≠
≠  y
y 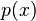 =
= 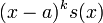 . Si
. Si 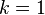 , entonces
, entonces  recibe el nombre de raíz simple.
recibe el nombre de raíz simple.
 un campo y
un campo y 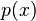 un polinomio de una variable con coeficientes en
un polinomio de una variable con coeficientes en  . Un elemento
. Un elemento  ∈
∈  se llama raíz de multiplicidad
se llama raíz de multiplicidad  de
de 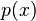 si existe un polinomio
si existe un polinomio  tal que
tal que 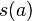 ≠
≠  y
y 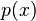 =
= 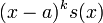 . Si
. Si 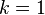 , entonces
, entonces  recibe el nombre de raíz simple.
recibe el nombre de raíz simple.
Por ejemplo el polinomio  tiene
tiene  y
y  como raíces, y puede escribirse como
como raíces, y puede escribirse como 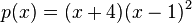 . Esto significa que
. Esto significa que  es una raíz de multiplicidad
es una raíz de multiplicidad  , y
, y  es una raíz 'simple' (multiplicidad
es una raíz 'simple' (multiplicidad  ).
).
 tiene
tiene  y
y  como raíces, y puede escribirse como
como raíces, y puede escribirse como 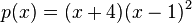 . Esto significa que
. Esto significa que  es una raíz de multiplicidad
es una raíz de multiplicidad  , y
, y  es una raíz 'simple' (multiplicidad
es una raíz 'simple' (multiplicidad  ).
).Multiplicidad de cero de una función
de Sea  un intervalo de R y
un intervalo de R y  una función de
una función de  a R o C y
a R o C y  ∈
∈  sea un cero de
sea un cero de  , por ejemplo, un punto tal que
, por ejemplo, un punto tal que  . El punto
. El punto  toma el nombre de cero de multiplicidad
toma el nombre de cero de multiplicidad  de
de  si existe un número real
si existe un número real 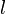 ≠
≠  tal que
tal que
 un intervalo de R y
un intervalo de R y  una función de
una función de  a R o C y
a R o C y  ∈
∈  sea un cero de
sea un cero de  , por ejemplo, un punto tal que
, por ejemplo, un punto tal que  . El punto
. El punto  toma el nombre de cero de multiplicidad
toma el nombre de cero de multiplicidad  de
de  si existe un número real
si existe un número real 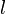 ≠
≠  tal que
tal que
De forma más general, sea  una función de un subconjunto abierto
una función de un subconjunto abierto  de un espacio vectorial con norma
de un espacio vectorial con norma  en un espacio vectorial con norma
en un espacio vectorial con norma  , y sea
, y sea  ∈
∈  cero de
cero de , por ejemplo, un punto tal que
, por ejemplo, un punto tal que  =
=  . El punto
. El punto  recibe el nombre de cero de multiplicidad
recibe el nombre de cero de multiplicidad  de
de  si existe un número real
si existe un número real 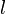 ≠
≠  tal que
tal que
 una función de un subconjunto abierto
una función de un subconjunto abierto  de un espacio vectorial con norma
de un espacio vectorial con norma  en un espacio vectorial con norma
en un espacio vectorial con norma  , y sea
, y sea  ∈
∈  cero de
cero de , por ejemplo, un punto tal que
, por ejemplo, un punto tal que  =
=  . El punto
. El punto  recibe el nombre de cero de multiplicidad
recibe el nombre de cero de multiplicidad  de
de  si existe un número real
si existe un número real 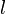 ≠
≠  tal que
tal que
El punto  se llama cero de multiplicidad ∞ de
se llama cero de multiplicidad ∞ de  si para cada
si para cada  , se cumple que
, se cumple que
 se llama cero de multiplicidad ∞ de
se llama cero de multiplicidad ∞ de  si para cada
si para cada  , se cumple que
, se cumple que
Ejemplo 1. Dado que
0 es un cero de multiplicidad 1 de la función seno.
Ejemplo 2. Dado qué
0 es un cero de multiplicidad 2 de la función  .
.
 .
.
Ejemplo 3. Considérese la función  de R en R tal que
de R en R tal que  y que
y que  cuando
cuando  ≠
≠  . Entonces, dado que
. Entonces, dado que
 de R en R tal que
de R en R tal que  y que
y que  cuando
cuando  ≠
≠  . Entonces, dado que
. Entonces, dado que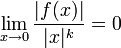 para todo
para todo  ∈ N
∈ N
0 es un cero de multiplicidad ∞ para la función  .
.
 .
.En análisis complejo
Sea  una raíz de una función holomorfa
una raíz de una función holomorfa  , y
, y  el último entero positivo
el último entero positivo  tal que, la
tal que, la  ésima derivada de
ésima derivada de  evaluada en
evaluada en  es diferente de cero. Entonces la serie de potencias de
es diferente de cero. Entonces la serie de potencias de  sobre
sobre  empieza con el término
empieza con el término  ésimo, y
ésimo, y  entonces tiene raíz de multiplicidad (o “orden”)
entonces tiene raíz de multiplicidad (o “orden”)  . Si
. Si 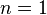 , la raíz recibe el nombre de raíz simple (Krantz 1999, p. 70).
, la raíz recibe el nombre de raíz simple (Krantz 1999, p. 70).
 una raíz de una función holomorfa
una raíz de una función holomorfa  , y
, y  el último entero positivo
el último entero positivo  tal que, la
tal que, la  ésima derivada de
ésima derivada de  evaluada en
evaluada en  es diferente de cero. Entonces la serie de potencias de
es diferente de cero. Entonces la serie de potencias de  sobre
sobre  empieza con el término
empieza con el término  ésimo, y
ésimo, y  entonces tiene raíz de multiplicidad (o “orden”)
entonces tiene raíz de multiplicidad (o “orden”)  . Si
. Si 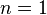 , la raíz recibe el nombre de raíz simple (Krantz 1999, p. 70).
, la raíz recibe el nombre de raíz simple (Krantz 1999, p. 70).
método de la fase estacionaria o aproximación de fase estacionaria es un principio básico del análisis asintótico, se aplica a las integrales oscilatorias, una clase de integrales de Fourier del tipo.
definidas en el espacio n-dimensional Rn, donde i es la unidad imaginaria. Aquí f y g son funciones continuamente diferenciables que toman valores reales. El papel de la función g es para asegurar la convergencia, es decir, g es una función test. El gran parámetro real k se considera en el límite cuando k → ∞.
Conceptos básicos
La idea principal de los métodos de la fase estacionaria se basa en la cancelación de sinusoides cuando la fase varía rápidamente. Si muchas sinusoides tienen la misma fase y son sumadas, se tendrá una suma constructiva. Si, sin embargo, estas mismas sinusoides tienen fases que cambian rápidamente a medida que cambia la frecuencia, se tendrá una suma destructiva.
Un ejemplo
Consideremos la función
El término de fase en esta función,  es "estacionario" cuando
es "estacionario" cuando
 es "estacionario" cuando
es "estacionario" cuando
o de modo equivalente,
Las soluciones de esta ecuación producen frecuencias dominantes 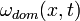 for a given
for a given  and
and  . Si expandimos
. Si expandimos  en una serie de Taylor sobre
en una serie de Taylor sobre  y anulamos los términos de orden superior a
y anulamos los términos de orden superior a 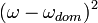 ,
,
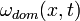 for a given
for a given  and
and  . Si expandimos
. Si expandimos  en una serie de Taylor sobre
en una serie de Taylor sobre  y anulamos los términos de orden superior a
y anulamos los términos de orden superior a 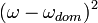 ,
,
Cuando  es relativamente grande, incluso una pequeña diferencia
es relativamente grande, incluso una pequeña diferencia  generará oscilaciones rápidas dentro de la integral, lo que lleva a la cancelación. Por lo tanto podemos extender los límites de la integración más allá del límite para un desarrollo de Taylor. Si duplicamos la contribución real de las frecuencias positivas de la transformación para tener en cuenta las frecuencias negativas,
generará oscilaciones rápidas dentro de la integral, lo que lleva a la cancelación. Por lo tanto podemos extender los límites de la integración más allá del límite para un desarrollo de Taylor. Si duplicamos la contribución real de las frecuencias positivas de la transformación para tener en cuenta las frecuencias negativas,
 es relativamente grande, incluso una pequeña diferencia
es relativamente grande, incluso una pequeña diferencia  generará oscilaciones rápidas dentro de la integral, lo que lleva a la cancelación. Por lo tanto podemos extender los límites de la integración más allá del límite para un desarrollo de Taylor. Si duplicamos la contribución real de las frecuencias positivas de la transformación para tener en cuenta las frecuencias negativas,
generará oscilaciones rápidas dentro de la integral, lo que lleva a la cancelación. Por lo tanto podemos extender los límites de la integración más allá del límite para un desarrollo de Taylor. Si duplicamos la contribución real de las frecuencias positivas de la transformación para tener en cuenta las frecuencias negativas,
Esto se integra como
Etapas de reducción
La primera afirmación general importante del principio en cuestión establece que el comportamiento asintótico de I(k) depende sólo de los puntos críticos de f. Si por causa de g la integral se localiza en una región del espacio donde f no tiene un punto crítico, el resultado de la integral tiende a 0 cuando la frecuencia de las oscilaciones se toman hasta el infinito. Véase, por ejemplo, el lema de Riemann-Lebesgue.
La segunda afirmación es que, cuando f es una función de Morse, de modo que los puntos singulares de f sean puntos críticos no degenerados y aislados, entonces la cuestión se reduce al caso n = 1. De hecho, a continuación, la elección de g se puede hacer para dividir la integral en casos con un solo punto crítico de P en cada uno de ellos. En ese punto, porque la matriz hessiana en P es por suposición distinta de 0, se aplica el lema de Morse. Mediante un cambio de coordenadas f podrá ser sustituido por
- x12 + ….+ xj2 − xj + 12 − xj + 22 − … − xn2.
El valor de j está dado por la signatura de la matriz hessiana de f en P. En cuanto a g, el caso esencial es que g es un producto de funciones de activación (bump function) de xi. Si se asume ya sin pérdida de generalidad que P es el origen, tomamos una función de activación continuamente diferenciable h con valor 1 en el intervalo [-1,1] y que rápidamente tiende a 0 fuera de ella.
Tomemos
- g(x) = Π h(xi).
Por tanto el teorema de Fubini reduce I(k) a un producto de integrales sobre la línea real, como
con f(x) = x2 o −x2. El caso con el signo menos es el complejo conjugado del caso con el signo más, por lo que hay esencialmente una estimación asintótica necesaria.
De esta manera asintótica se pueden encontrar soluciones para las integrales oscilatorias de las funciones de Morse. El caso degenerado requiere técnicas adicionales. Véase, por ejemplo, la función de Airy.
Caso unidimensional
La definición esencial es esta:
De hecho por integración de contorno se puede demostrar que el término principal en el lado derecho de la ecuación es el valor de la integral en el lado izquierdo, extendida sobre el intervalo [- ∞, ∞]. Por eso, la cuestión es la estimación de la integral sobre, por ejemplo, [1, ∞].1
Este es el modelo para todas las integrales de una dimensión I(k) con f teniendo un único punto crítico no degenerado en el que f tiene segunda derivada mayor que 0. De hecho, el caso modelo tiene como segunda derivada 2 en 0. Con el fin de escalar con k, teniendo en cuenta que la sustitución de k por ck donde c es una constante es la misma que escalar x mediante √ c. De ello se deduce que para los valores generales de f "(0)> 0, el factor √ (π / K) se convierte en
Para f "(0) <0 antes.="" como="" compleja="" conjugada="" f="" la="" mencion="" p="" rmula="" se="" usa="">

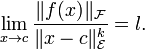



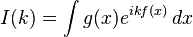
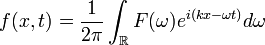

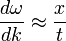
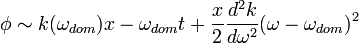
![f(x, t) = \frac{1}{2\pi} 2 \mbox{Re}\left\{ \exp\left[i\left[k(\omega_{dom})x-\omega_{dom}t\right]\right] \left|F(\omega_{dom})\right| \int_{\mathbb{R}}\exp\left[i\frac{x}{2}\frac{d^2k}{d\omega^2}(\omega-\omega_{dom})^2\right]d\omega\right\}](https://upload.wikimedia.org/math/e/8/6/e86e9e87dec31fcba8ce63d29fcac539.png)
![f(x, t) \sim \frac{\left|F(\omega_{dom})\right|}{\pi} \sqrt{ \frac{2\pi}{x\left|\frac{d^2k}{d\omega^2}\right|}} \cos\left[ k(\omega_{dom})x - \omega_{dom}t \pm \frac{\pi}{4}\right]](https://upload.wikimedia.org/math/e/9/6/e96a51c4902268e495d035ffcd9dcb18.png)
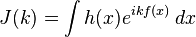


No hay comentarios:
Publicar un comentario