jueves, 15 de octubre de 2015

Análisis matemático


sistemas no lineales representan sistemas cuyo comportamiento no es expresable como la suma de los comportamientos de sus descriptores. Más formalmente, un sistema físico, matemático o de otro tipo es no lineal cuando las ecuaciones de movimiento, evolución o comportamiento que regulan su comportamiento son no lineales. En particular, el comportamiento de sistemas no lineales no está sujeto al principio de superposición, como lo es un sistema lineal.
En diversas ramas de las ciencias la no linealidad es la responsable de la comportamientos complejos y, frecuentemente, impredictibles o caóticos. La no linealidad frecuentemente aparece ligada a la autointeracción, el efecto sobre el propio sistema del estado anterior del sistema. En física, biología o economía la no linealidad de diversos subsistemas es una fuente de problemas complejos, en las últimas décadas la aparición de los ordenadores digitales y la simulación numérica ha disparado el interés científico por los sistemas no lineales, ya que por primera vez muchos sistemas han podido ser investigados de manera más o menos sistemática.

Introducción

La linealidad de un sistema permite a los investigadores hacer ciertas suposiciones matemáticas y aproximaciones, permitiendo un cálculo más sencillo de los resultados. Ya que los sistemas no lineales no son iguales a la suma de sus partes, usualmente son difíciles (o imposibles) de modelar, y sus comportamientos con respecto a una variable dada (por ejemplo, el tiempo) es extremadamente difícil de predecir.
Algunos sistemas no lineales tienen soluciones exactas o integrables, mientras que otros tienen comportamiento caótico, por lo tanto no se pueden reducir a una forma simple ni se pueden resolver. Un ejemplo de comportamiento caótico son las olas gigantes. Aunque algunos sistemas no lineales y ecuaciones de interés general han sido extensamente estudiados, la vasta mayoría son pobremente comprendidos.

Sistemas lineales

En matemáticas una función lineal es aquella que satisface las siguientes propiedades. ya que en un sistema tiene que poner en conjunto de dos o más ecuaciones.
  1. Aditividad: f(x + y) = f(x) + f(y) \
  2. Homogeneidad: f(\alpha\,x) = \alpha\,f(x) \
Estas dos reglas tomadas en conjunto se conocen como Principio de superposición.

Sistemas no lineales

Las ecuaciones no lineales son de interés en física y matemáticas debido a que la mayoría de los problemas físicos son implícitamente no lineales en su naturaleza. Ejemplos físicos de sistemas lineales son relativamente raros. Las ecuaciones no lineales son difíciles de resolver y dan origen a interesantes fenómenos como la teoría del caos. Una ecuación lineal puede ser descrita usando un operador lineal, L. Una ecuación lineal en algún valor desconocido de u tiene la forma
Lu = 0 \,
Una ecuación no lineal es una ecuación de la forma:
F(u)=0 \,
Para algún valor desconocido de u.
Para poder resolver cualquier ecuación se necesita decidir en qué espacio matemático se encuentra la solución u. Podría ser que u es un número real, un vector o, tal vez, una función con algunas propiedades.
Las soluciones de ecuaciones lineales pueden ser generalmente descritas como una superposición de otras soluciones de la misma ecuación. Esto hace que las ecuaciones lineales sean fáciles de resolver.
Las ecuaciones no lineales son mucho más complejas, y mucho más difíciles de entender por la falta de soluciones simples superpuestas. Para las ecuaciones no lineales las soluciones generalmente no forman un espacio vectorial y, en general, no pueden ser superpuestas para producir nuevas soluciones. Esto hace el resolver las ecuaciones mucho más difícil que en sistemas lineales.

Herramientas para la solución de ciertas ecuaciones no lineales

Al día de hoy, existen muchas herramientas para analizar ecuaciones no lineales, por mencionar algunas tenemos: dinámica de sistemas, teorema de la función implícitay la teoría de la bifurcación
  • Malinietski G.G. 2006. Fundamentos matemáticos de la sinergética. Caos, estructuras y simulación por ordenador. [1].

Ejemplos de sistemas no lineales

Una importante colección de sistemas físicos y de otro tipo parecen venir descritos por sistemas de ecuaciones de evolució temporal que de hecho son ecuaciones diferenciales no lineales, algunos ejemplos notorios de no linealidad son los siguientes:












operador hermítico (también llamado hermitiano) definido sobre un espacio de Hilbert es un operador lineal que, sobre un cierto dominio, coincide con su propio operador adjunto. Una propiedad importante de estos operadores es que sus autovalores son siempre números reales.
Cuando el dominio de un operador hermítico y el de su operador adjunto coinciden totalmente se dice entonces que es un operador autoadjunto. En un espacio de Hilbert de dimensión finita todo operador hermítico es además autoadjunto.

Dimensión finita

En espacios de Hilbert de dimensión finita todo operador hermítico es además autoadjunto. Además en dimensión finita un operador hermítico fijada una base ortogonalviene dado por una matriz hermítica y diagonalizable.
Una matriz es hermítica o autoadjunta cuando es igual a su propia adjunta y es antihermítica cuando es igual a su traspuesta conjugada multiplicada por -1.
Sobre espacios vectoriales reales, las matrices hermíticas coinciden con las matrices simétricas y las antihermíticas con las antisimétricas. Estos operadores se pueden representar como una matriz diagonal (en una base ortonormal) de números reales. Este concepto se puede generalizar a un espacio de Hilbert de dimensión arbitraria.

Dimensión infinita

En espacios de dimensión infinita, como los espacios de Hilbert que aparecen en análisis funcional y en mecánica cuántica, un operador puede ser hermítico pero no autoadjunto (aunque todos los operadores autoadjuntos son evidentemente hermíticos).
El interés en los operadores en mecánica cuántica se debe a que en la formulación de Dirac-von Neumann, los posibles valores de los observables físicos o magnitudes físicas, son precisamente los autovalores de ciertos operadores que representan la magnitud física. Así pues el que un operador pueda ser interpretado como una magnitud físicamente medible requiere que sus autovalores sean números reales, condición que queda garantizada si los observables se representan por operadores hermíticos.

Operadores autoadjuntos

La consecuencia más importante de que un operador hermítico sea además autoadjunto es que entonces se le puede aplicar el teorema de descomposición espectral. Para un operador hermítico en un espacio de Hilbert de dimensión infinita en general no existe la "resolución espectral de la identidad", que sí está garantizada para operadores autoadjuntos.
Todos los operadores importantes de la mecánica cuántica como la posición, el momentum, el momento angular, la energía o el espín se representan como operadores autoadjuntos en un dominio denso espacio de Hilbert L^2(\mathbb{R}^3). Otro operador particularmente importante para un sistema cuántico es el operador hamiltoniano definido por:
\hat{H} \psi = - \frac{\hbar^2}{2 m} \Delta \psi + V \psi

que, como observable, corresponde a la energía total de una partícula de masa m en un campo de potencial V y que para la mayoría de los sistemas es un operador no-acotado, relacionado con el hecho de que en esos sistemas no existe un valor máximo para la energía que puede tener una partícula.
Es interesante notar que normalmente los operadores no acotados, como el operador Hamiltoniano no están definidos en todo el espacio, sino solamente en un dominio denso. Los estados sobre los que no está definidos corresponderían a estados de "energía infinita". Por ejemplo para el oscilador armónico cuántico unidimensional en que V(x) = x2, el operador hamiltoniano no está definido sobre el estado cuántico:
\psi(x) = \frac{6}{\pi^2} \sum_{k=1}^\infty \frac{\psi_k(x)}{k}

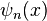Donde \psi_n(x) son los estados estacionarios normalizados, siendo la energía de cada uno de ellos \hat{H}\psi_n(x) = \hbar\omega[n+(1/2)]\cdot\psi_n(x). Es sencillo ver que el hamiltoniano no está definido para ese estado:
\hat{H}\psi(x) = \frac{6}{\pi^2} \sum_{k=1}^\infty \frac{\hat{H}\psi_k(x)}{k} = \frac{6}{\pi^2} \sum_{k=1}^\infty \frac{k+1/2}{k}\psi_k(x) = \infty

Ejemplos

Operador hermítico en dimensión finita

Matriz hermítica A+ := (A*)T= A. Los elementos de la diagonal deben ser reales, por ejemplo:
A \quad = \begin{pmatrix} 13 & 3-4i \\ 3+4i & 2 \end{pmatrix} \quad \qquad \Rightarrow \qquad A^T \quad = \begin{pmatrix} 13 & 3+4i \\ 3-4i & 2 \end{pmatrix} = A^*

Es interesante notar que la matriz inversa de una matriz hermítica es también hermítica:
A^{-1} = \begin{pmatrix} 2 & -3+4i \\ -3-4i & 13 \end{pmatrix}\qquad \Rightarrow \qquad \left(A^{-T}\right)= \begin{pmatrix} 2 & -3-4i \\ -3+4i & 13 \end{pmatrix} = (A^*)^{-1}


Operadores hermíticos en dimensión infinita

El caso de la dimensión infinita es más complicado ya que un operador hermítico no necesariamente es autoadjunto, a diferencia de lo que sucede en dimensión finita. Como los espacios de Hilbert de la descripción cuántica de los sistemas reales suelen ser de dimensión infinita, el caso de dimensión infinita tiene un interés físico directo.
Un ejemplo bien conocido es el momento lineal en dirección radial, que desde el punto de vista clásico es una magnitud física medible, pero su generalización cuántico es un operador hermítico pero no autoadjunto. Consecuentemente, no existe un experimento cuántico que pueda medir genuinamente el momento radial, al no ser unobservable.








 partición Π de un intervalo cerrado [a, b] en los números reales es una secuencia finita de la forma
a = x0 < x1 < x2 <... < xn = b.
Estas particiones se utilizan en la teoría de la integral de Riemann y la integral de Riemann-Stieltjes.

Refinamiento de una partición

Se dice que una partición Π' es más fina que una partición Π cuando Π es un subconjunto de Π', es decir, cuando la partición Π' tiene los mismos puntos que Π y posiblemente alguno más.

Ejemplos

Un ejemplo de partición sería el siguiente:
Dado el intervalo [1, 2], una partición de dicho intervalo sería
Π = {1, \frac{3}{2},\frac{5}{3}, 2}.
Otra posible partición para el mismo intervalo sería
Π' = {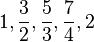1, \frac{3}{2},\frac{5}{3}, \frac{7}{4}, 2}, con Π' más fina que Π.
Publicado por en

No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)