El Teorema de Robbins, nombrado en honor a Herbert Robbins establece:
|
en donde la condición de Riemann super-integrabilidad establece:
En matemática, la torsión tiene varios significados, en general sin relación el uno con el otro:
donde [u, v] es el corchete de Lie de los dos campos vectoriales. Las conexiones libres de torsión son las que se consideran más frecuentemente -la conexión de Levi-Civita presupone tener torsión cero, por ejemplo-.
Transformada de Fourier de Tiempo Corto (Short-time Fourier transform, STFT) o Transformada de Fourier de Término Reducido (short-term Fourier transform) está relacionada con la transformada de Fourier usada para determinar el contenido en frecuencia sinusoidal y de fase en secciones locales de una señal así como sus cambios con respecto al tiempo. STFT de tiempo continuo
Simplemente, en el caso del tiempo continuo, la función a ser transformada se multiplica por una función ventana que solo es diferente de cero por un pequeño período. La trasformada de Fourier (una función de una sola dimensión) de la señal resultante es tomada como la ventana que se desliza a lo largo del eje del tiempo, resultando una representación en dos dimensiones de la señal. Matemáticamente, se escribe como:
donde w(t) es la función ventana, comúnmente una ventana de Hann o ventana campana Gaussiana centrada en cero, y x(t) es la señal a ser transformada, x(t, w) es esencialmente la Transformada de Fourier de x(t)x(t - τ), una función compleja que representa la fase y magnitud de la señal sobre tiempo y frecuencia. A menudo se emplea la fase instantánea junto con el eje del tiempo τ y el eje de la frecuencia w para suprimir cualquier discontinuidad por salto en la fase resultante en la STFT. El índice de tiempo τ normalmente se considera un tiempo "lento" y usualmente no se expresa con tan alta resolución como con el tiempo t
STFT en tiempo discreto
Véase también: transformada modificada discreta del coseno
En el caso del tiempo discreto, la información a ser transformada podría ser dividida en pedazos o tramas (que usualmente se traslapan unos con otros, para reducir irregularidades en la frontera). Cada pedazo una transformación de Fourier, y el resultado complejo se agrega a una matriz, que almacena magnitud y fase para cada punto en tiempo y frecuencia. Esto se puede expresar así:
Donde, x[n] es la señal y w[n] es la ventana. En este caso m es disctreta y ω es contínua, pero en la mayoría de aplicaciones típicas la STFT se hace en un computador usando la Tranasformada Rápida de Fourier, así ambas variables son discretas y cuantizadas. De nuevo, el índice de tiempo discreto m es normalmente considerado como un tiempo "lento" y usualmente no se expresa con tan alta resolución como con el tiempo n.
La magnitud cuadrada de la STFT origina el espectrograma de la función:
Vea también la transformada modificada discreta del coseno (MDCT), que está también relacionada con la transformada de Fourier y que usa ventanas traslapadas.
STFT inversa
La STFT es invertible, esto es, la señal original puede ser recuperada de la transformación por medio de la STFT inversa. La forma más ampliamente aceptada de invertir la STFT es usando el método suma solapada (overlap-add, OLA), que también permite modificar al espectro complejo de STFT. Esto lo hace un método de procesamiento de señal versátil, referido como el método de solapamiento y suma con modificaciones.
STFT en tiempo continuo
Dado el ancho y definición de la función ventana w(t), se requiere inicialmente que el área de la función ventana sea ajustada así que
Es fácil deducir que
y
La transformada de Fourier contínua es
Substituyendo x(t) de arriba:
Cambiando el orden de integración:
Por lo que la Transformada de Fourier puede ser vista como una suma coherente de fases de todos los STFTs de x(t), Debido a que la transformada inversa de Fourier es
entonces x(t) puede ser recuperada de X(τ,ω) como
o
Se puede ver que, al comparar arriba que la ventana de "grano" o "wavelet" de x(t) es
la transformada de Fourier inversa de X(τ, ω) para una τ fija.
La STFT en tiempo discretoCuestiones de la resolución
Uno de los problemas del STFT es que tiene una resolución fija. El ancho de la función de ventana está relacionado con el como la señal es representada, esto determina si hay buena resolución en frecuencia (las componentes de frecuencia que están cerca pueden ser separadas) o buena resolución en tiempo (el tiempo en cuyas frecuencias cambian). Una ventana amplia da una mejor resolución en frecuencia pero también una pobre resolución en el tiempo. Una ventana angosta da una buena resolución en el tiempo pero una pobre resolución en frecuencia. Estas son llamadas transformadas de banda angosta y de banda amplia, respectivamente.
Esta es una de las razones de la creación de la transformada wavelet (o análisis multiresolución en general), que puede dar una buena resolución en el tiempo para eventos de alta frecuencia y buena resolución en frecuencia para eventos de baja frecuencia, que es el tipo de análisis mejor utilizado para muchas señales reales.
Esta propiedad está relacionada con el principio de incertidumbre de Heisenberg, pero no es una relación directa. El producto de la desviación estándar en el tiempo y en la frecuencia es limitado. La frontera del principio de incertidumbre (la mejor resolución en frecuencia de ambas) es alcanzado por una función de ventana Gausiana, debido a que el Gausiano minimiza el principio de incertidumbre de Fourier.
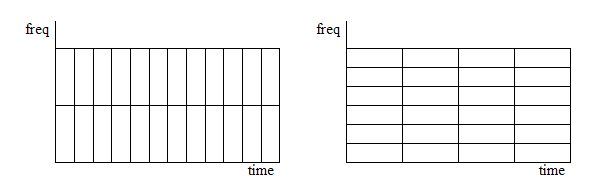
Uno puede considerar la STFT para ventanas de tamaño variable como si fuera un dominio en dos dimensiones (tiempo, frecuencia), como se ha ilustrado en el ejemplo de abajo, que puede ser calculado al variar el tamaño de la ventana. De todas, maneras, esto no es más que una estricta representación del tiempo y la frecuencia.
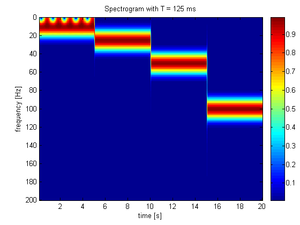
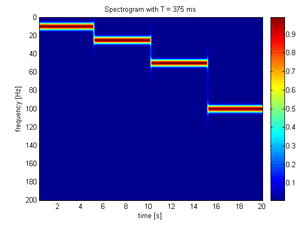
Ejemplo
Usando la siguiente muestra de señal x(t) que está compuesta por un conjunto de 4 formas de onda sinusoidales unidas en secuencia. Cada forma de onda está únicamente compuesta de una de cuatro frecuencias (10, 25, 50, 100 Hz). La definición de x(t) es.
Entonces, muestreado a 400 Hz se obtuvo el siguiente espectrograma:
La ventana de 25 ms nos permite identificar un tiempo preciso en el cual la señal cambia pero los cambios precisos en la frecuencia son difíciles de identificar- En el otro extremo de la escala, la ventana de 1000 ms permite que las frecuencias sean vistas de forma precisa pero el tiempo entre los cambios de frecuencia es borroso. Explicación
También puede ser explicado con referencia al muestreo y a la frecuencia de Nyquist
Tome una ventana de N muestras del valor real de una señal arbitraria con una tasa de muestreo de fs. Tomando la transformada de Fourier se produce N coeficientes complejos. De estos coeficientes solo la mitad son útiles (el último N/2 siendo el complejo conjugado del primer N/2 en orden inverso, ya que este es el valor real de una señal).
Estos N/2 coeficientes representan las frecuencias 0 a fs/2 (Nyquist) y dos coeficientes consecutivos son espaciados aparte por fs/N Hz.
Para incrementar la resolución en frecuencia de la ventana, la frecuencia de espaciado de los coeficientes necesita ser reducida. Hay solo dos variables, pero el disminuir fs (y mantener N constante) causará que el tamaño de la ventana aumente, debido a que ahora hay menos muestras por unidad de tiempo. La otra alternativa es incrementar N, pero esto causa de nuevo que el tamaño de la ventana se incremente. Cualquier intento de incrementar la resolución en frecuencia causa un mayor tamaño de la ventana y por lo tanto una reducción en la resolución del tiempo y viceversa.
Aplicación
transformada de Legendre si cada una de sus primerasderivadas son función inversa de la otra:
Se dice entonces de f y g que están relacionadas por una transformada de Legendre. Son unívocas hasta una constante aditiva que normalmente se fija mediante el requisito adicional de que
Motivación
En ciertos problemas matemáticos o físicos es deseable expresar una cierta magnitud f (como la energía interna) como función diferente g en que los argumentos sean precisamente las derivadas de la función respecto a las antiguas variables. Si designamos al nuevo argumento y se tiene que la relación con el viejo argumento es y =df/dx.
La transformación de Legendre permite la construcción anterior, mediante el teorema de la función implícita, de una nueva función g que satisface los requisitos anteriores: Donde 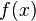 es la función original y es la función original y  es el operador transformada de Legendre. Una función es el operador transformada de Legendre. Una función 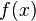 admite transformada de Legendre, si existe su derivada segunda y no se anula nunca: admite transformada de Legendre, si existe su derivada segunda y no se anula nunca:En esas condiciones el Teorema de la Función Implícita aplicado a la función: garantiza que existe la función diferenciable, x(y). Aplicaciones a los potenciales termodinámicos
La estrategia tras el uso de las transformadas de Legendre es desplazar la dependencia de una función de una variable independiente a otra (la derivada de la función original con respecto a su variable independiente) tomando la diferencia entre la función original y su producto. Se usan para realizar transformaciones entre los diversos potenciales termodinámicos.
Por ejemplo, mientras las energía interna es una función explícita de las variables extensivas, entropía, volumen (y composición química)
la entalpía es otra función de estado que puede construirse como la transformada de Legendre de la energía interna U con respecto a −PV
se convierte en función de la entropía y la cantidad intensiva, presión, como variables naturales, y es útil cuando la P (externa) es constante. La transformación estará definida siempre que sea posible "invertir" el volumen en función de la presión y la entropía, cosa que requiere que:
Donde βs es la compresibilidad adiabática.
Las energías libres (Helmholtz y Gibbs se obtienen mediante sucesivas transformadas de Legendre, eliminando TS (de U y H, respectivamente), cambiando la dependencia de la entropía S a su variable conjugada intensiva temperatura T, y es útil cuando ésta es constante.
Aplicaciones a la electrotecnia
Otro ejemplo de la física: considere un condensador de placas plano-paralelas cuyas placas puedan aproximarse o alejarse una de otra, intercambiando trabajo confuerzas mecánicas externas que mantienen la separación de las placas (análogo a un gas en un cilindro con un pistón. Queremos que la fuerza atractiva f entre las placas sea función de la separación variable x (Los dos vectores espaciales apuntan en sentidos opuestos). Si las cargas de las placas se mantienen constantes mientras se mueven, la fuerza es el gradiente negativo de la energía electrostática.
Sin embargo, si se mantiene constante el voltaje entre las placas V conectando una batería, que es una reserva de carga a diferencia de potencial constante, la fuerza se convierte en el gradiente negativo de la transformada de Legendre
Las dos funciones resultan ser negativas sólo por la linealidad de la capacitancia. Por supuesto, para una carga, voltaje y distancia dadas, la fuerza estática debe ser la misma mediante cualquier cálculo ya que las placas no pueden "saber" qué se mantendrá constante mientras se mueven.
Aplicaciones en mecánica clásica
En mecánica clásica se usa una transformada de Legendre para derivar la formulación hamiltoniana partiendo de la formulación lagrangiana, y viceversa.
Eso es posible, puesto que la función lagrangiana o lagrangiano que aparece en la formulación lagrangiana es un función explícita de las coordenadas posicionales qj y las velocidades generalizadas dqj /dt (y tiempo). Por su parte la función de Hamilton o hamiltoniano que aparece en la formulación hamiltoniana es función explícita de las coordenadas posicionales y los momentos. El punto importante es que los momentos pueden ser obtenidos como derivadas del lagrangiano:
con lo cual estamos en la condiciones para construir el hamiltoniano a partir del lagrangiano (siempre y cuando además se cumpla la condición requerida por el teorema de la función implícita). En esas condiciones el hamiltoniano viene dado como transformación de Legendre del lagrangiano: La transformación anterior es posible que el lagrangiano en cada punto del espacio de configuración sea una forma bilineal cuadrática no-degenerada de las velocidades puesto que en ese caso, la condición de existencia de la inversa  está automáticamente garantizada por el teorema de la función implícita ya que: está automáticamente garantizada por el teorema de la función implícita ya que:Cada una de las dos formulaciones de la mecánica clásica tiene su propio campo de aplicación, tanto en los fundamentos teóricos del tema como en la práctica, dependiendo de la sencillez de cómputo de un problema en particular. Las coordenadas no tienen necesariamente que ser rectilíneas o cartesinas, sino también ángulos, etc. Una opción óptima tomaría ventaja de las simetrías físicas reales. Ejemplos
La función exponencial ex tiene a x ln x − x como transformada de Legendre, dado que las primeras derivadas respectivas ex y ln x son inversa una de la otra. Este ejemplo muestra que los dominios respectivos de una función y su transformada de Legendre no tienen por qué coincidir.
De forma similar, la forma cuadrática
donde A es una matriz simétrica invertible de n por n, tiene por transformada de Legendre a
Transformada de Legendre en una dimensión
En una dimensión, se puede encontrar la transformada de Legendre de una función f : R → R con primera derivada invertible usando la fórmula
Se puede ver esto como la integración de ambos lados de la condición definitoria restringida a una dimensión
de x0 a x1, haciendo uso del teorema fundamental del cálculo en el lado izquierdo y sustituyendo
en el lado derecho para encontrar
donde g′(y0) = x0, g′(y1) = x1. Usando integración por partes la última integral se simplifica como
Por tanto,
Dado que el lado izquierdo de esta ecuación sólo depende de x1 y el derecho sólo de x0, tienen que evaluar a la misma constante.
Resolviendo para g y escogiendo que C sea cero obtenemos la fórmula mencionada anteriormente.
Interpretación geométrica
Para una función estrictamente convexa, se puede interpretar la transformada de Legendre como una correspondencia entre la gráfica de la función y la familia detangentes de la gráfica. (Para una función de una variable, las tangentes están bien definidas en todos los puntos excepto para un conjunto numerable de ellos, dado que una función convexa es diferenciable en todos sus puntos excepto en una cantidad numerable de ellos.)
La ecuación de una línea con pendiente m y punto b de corte del eje de las ordenadas la da
Para que esta línea sea tangente a la gráfica de una función f en el punto (x0, f(x0)) se precisa que
y
f es estrictamente monótona ya que es la derivada de una función estrictamente convexa, y la segunda función se puede resolver para x0, permitiendo eliminar x0 de la primera, dejando el término b' de la tangente como función de su pendiente m:
Aquí f* denota la transformada de Legendre de f.
La familia de tangentes de la gráfica de f la da por tanto, parametrizada por m,
o, escrito de forma explícita, viene dada por las soluciones de la ecuación
La gráfica de la función original se puede reconstruir partiendo de esta familia de líneas como la envolvente de esta familia exigiendo que
Eliminando m de estas dos ecuaciones obtenemos
Identificando y con f(x) y reconociendo el lado derecho de la ecuación anterior como la transformada de Legendre de f*, encontramos que
Transformada de Legendre en más de una dimensión
Para una función real diferenciable sobre un subconjunto abierto U de Rn, el conjugado de Legendre del par (U, f) se define como el par (V, g), donde V es la imagen deU según la función gradiente Df, y g es la función sobre V dada por la fórmula
donde
es el producto escalar sobre Rn.
De forma alternativa, si X es un espacio vectorial real e Y es un espacio dual, entonces para cada punto
 e e  , existe una identificación natural de losespacios cotangentes T*Xx con Y y T*Yy con X. Si f es una función real diferenciable sobre X, entonces ∇f es una sección del fibrado cotangente T*X y como tal, podemos construir una correspondencia de X sobre Y. De forma similar, si g es una función real diferenciable sobre Y, ∇g define una correspondencia de Y sobre X. Si ambas correspondencias son inversas de la otra, decimos que tenemos una transformada de Legendre. , existe una identificación natural de losespacios cotangentes T*Xx con Y y T*Yy con X. Si f es una función real diferenciable sobre X, entonces ∇f es una sección del fibrado cotangente T*X y como tal, podemos construir una correspondencia de X sobre Y. De forma similar, si g es una función real diferenciable sobre Y, ∇g define una correspondencia de Y sobre X. Si ambas correspondencias son inversas de la otra, decimos que tenemos una transformada de Legendre.Más propiedades
En lo que sigue, la transformada de Legendre de una función f se denota como f*.
Propiedades de escalado
La transformada de Legendre tiene las siguientes propiedades de escala:
Se sigue de aquí que si una función es homogénea de grado r entonces su imagen bajo la transformada de Legendre es una función homogénea de grado s, donde 1/r + 1/s = 1.
Comportamiento ante traslaciónComportamiento ante inversiónComportamiento ante transformaciones lineales
Sea A una transformación lineal de Rn en Rm. Para cualquier función convexa f sobre Rn, tenemos
donde A* es el adjunto de A definido por
Una función convexa cerrada f es simétrica con respecto a un conjunto dado G de transformaciones lineales ortogonales,
si y sólo si f* es simétrica con respecto a G.
Convolución infimal
La convolución infimal de dos funciones f y g se define como
Sean f1, …, fm funciones convexas propias sobre Rn. Entonces
|

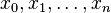 y
y  en el intervalo [a, b] que satisfagan
en el intervalo [a, b] que satisfagan ,
,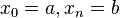 ,
,  y cada
y cada  está en el intervalo con puntos extremos
está en el intervalo con puntos extremos  (observando que los puntos no necesariamente están ordenados).
(observando que los puntos no necesariamente están ordenados).
![T(u,v)=\nabla_u v - \nabla_v u -[u,v] \,](https://upload.wikimedia.org/math/d/c/9/dc9b43bafcc76b57f3e98db1924fa75b.png)

![\mathbf{STFT} \left \{ x[n] \right \} \equiv X(m,\omega) = \sum_{n=-\infty}^{\infty} x[n]w[n-m]e^{-j \omega n}](https://upload.wikimedia.org/math/d/f/9/df9de933b6b30ef26f0b599f61389512.png)

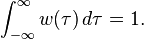

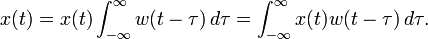
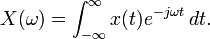
![X(\omega) = \int_{-\infty}^{\infty} \left[ \int_{-\infty}^{\infty} x(t) w(t-\tau) \, d\tau \right] \, e^{-j \omega t} \, dt](https://upload.wikimedia.org/math/8/2/6/8262d82b5dc191e824e1f873c31e6ad3.png)


![= \int_{-\infty}^{\infty} \left[ \int_{-\infty}^{\infty} x(t) w(t-\tau) \, e^{-j \omega t} \, dt \right] \, d\tau](https://upload.wikimedia.org/math/7/e/e/7ee2f316ceb3d0e9f524f8d538da972d.png)
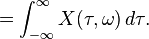
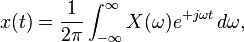

![x(t) = \int_{-\infty}^{\infty} \left[ \frac{1}{2 \pi} \int_{-\infty}^{\infty} X(\tau, \omega) e^{+j \omega t} \, d\omega \right] \, d\tau.](https://upload.wikimedia.org/math/d/d/4/dd4457409e90af6b68eb687c7cbbeb19.png)
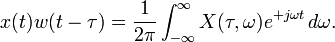
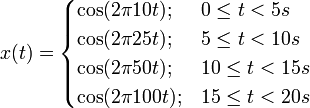



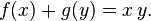

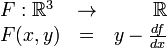

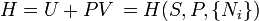
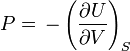
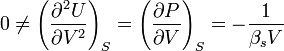
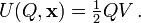









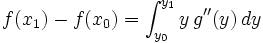


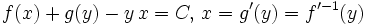


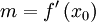



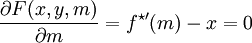



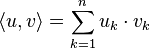


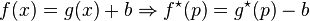
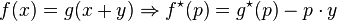
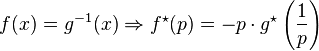





 es un número real, su valor absoluto es un número real no negativo definido de las dos siguientes maneras:
es un número real, su valor absoluto es un número real no negativo definido de las dos siguientes maneras: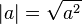
 es igual al máximo de {a, -a}.
es igual al máximo de {a, -a}. 
 está definido por:
está definido por: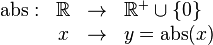
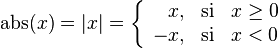
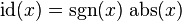

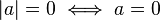


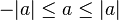

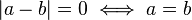
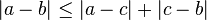








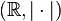 es un
es un 
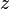 es la distancia
es la distancia  desde
desde  tienen el mismo valor absoluto.
tienen el mismo valor absoluto.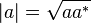 donde a* es el conjugado del número complejo a.
donde a* es el conjugado del número complejo a.

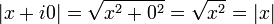

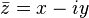

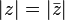

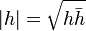
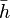 representa el
representa el
No hay comentarios:
Publicar un comentario