sumación de Borel es una generalización de la noción común de suma de una serie. En particular provee una definición de una cantidad que en numerosos aspectos se comporta formalmente como una suma, aún en el caso de que la serie sea divergente.
Definición
Sea
una serie de potencia formal en  .
.
 .
.
Se define la transformada de Borel  de
de  mediante
mediante
 de
de  mediante
mediante
Suponiendo que
 tiene un radio de convergencia no nulo como función de
tiene un radio de convergencia no nulo como función de 
 puede ser continuada en forma analítica a una función
puede ser continuada en forma analítica a una función 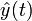 sobre toda la recta real positiva
sobre toda la recta real positiva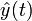 como mucho crece en forma exponencial a lo largo de la recta real
como mucho crece en forma exponencial a lo largo de la recta real
Entonces la suma de Borel de  está dada por la transformada de Laplace de
está dada por la transformada de Laplace de 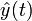 . La existencia de esta función esta garantizada por la condición (3) indicada previamente.
. La existencia de esta función esta garantizada por la condición (3) indicada previamente.
 está dada por la transformada de Laplace de
está dada por la transformada de Laplace de 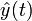 . La existencia de esta función esta garantizada por la condición (3) indicada previamente.
. La existencia de esta función esta garantizada por la condición (3) indicada previamente.Discusión
La suma de Borel de una serie es la transformada de Laplace de la suma de las anti-transformadas de Laplace término a término de la serie original. Si la transformada de Laplace de una serie infinita fuera igual a la suma de la transformada de Laplace término a término entonces la suma de Borel sería igual a la suma común. La suma de Borel es definida en muchas situaciones en las que la suma no esta definida. Expresándolo en términos llanos, permite darle un significado a la 'suma' de cierto tipo de series divergentes. La sumación de Borel es un ejemplo de un método de momento constante para sumar series.
Usos
La sumación de Borel es utilizada en la teoría de perturbaciones campo en el cual es común que los físicos requieran calcular la suma de series a pesar de que ellas puedan ser divergentes.
sumatorio de Ramanujan es una técnica inventada por el matemático indio Srinivasa Ramanujan para asignar una suma a una serie divergente infinita. A pesar de que el sumatorio de Ramanujan de una serie divergente no es una suma en el sentido tradicional, ésta tiene propiedades que las hacen matemáticamente útiles en el estudio de series infinitas divergentes, para las cuales la suma normal no está definida.
Desarrollo
El sumatorio de Ramanujan se desarrolla esencialmente usando propiedades de las sumas parciales, en lugar de tomar propiedades de la suma global, la cual no existe. Usando el método de Euler–Maclaurin junto con la regla de corrección que hace uso de los números de Bernoulli, se obtiene:
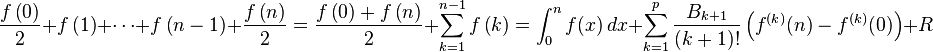
donde C es una constante específica de la serie a tratar. Su continuación analítica y los límites de la integral no fueron especificados por Ramanujan, pero se supone que son los mencionados arriba.. Comparando ambas fórmulas y asumiendo que R tiende a 0 y x tiende a infinito, se puede ver que, en un caso general, para funciones f(x) que no divergen en x = 0:
donde Ramanujan asumió que a = 0 . Tomando 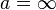 , normamente se puede recuperar la suma usual para series convergentes, así pues C(0) fue propuesta para su uso en la suma de la secuencia divergente.
, normamente se puede recuperar la suma usual para series convergentes, así pues C(0) fue propuesta para su uso en la suma de la secuencia divergente.
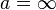 , normamente se puede recuperar la suma usual para series convergentes, así pues C(0) fue propuesta para su uso en la suma de la secuencia divergente.
, normamente se puede recuperar la suma usual para series convergentes, así pues C(0) fue propuesta para su uso en la suma de la secuencia divergente.Suma de series divergentes
Usando extensiones standard para series divergentes conocidas, Ramanujan calculó la «suma» de éstas. En particular, la suma 1 + 2 + 3 + 4 + · · ·+ n +· · · es
donde la notación  indica que es un sumatorio de Ramanujan. Esta expresión aparece originariamente en uno de los cuadernos de Ramanujan, sin ningún tipo de anotación que indicara que ésta se trataba de un sumatorio de Ramanujan.
indica que es un sumatorio de Ramanujan. Esta expresión aparece originariamente en uno de los cuadernos de Ramanujan, sin ningún tipo de anotación que indicara que ésta se trataba de un sumatorio de Ramanujan.
 indica que es un sumatorio de Ramanujan. Esta expresión aparece originariamente en uno de los cuadernos de Ramanujan, sin ningún tipo de anotación que indicara que ésta se trataba de un sumatorio de Ramanujan.
indica que es un sumatorio de Ramanujan. Esta expresión aparece originariamente en uno de los cuadernos de Ramanujan, sin ningún tipo de anotación que indicara que ésta se trataba de un sumatorio de Ramanujan.
Para potencias pares positivas, se obtiene:
y para potencias impares positivas ,se obtiene esta expresión, relacionada con los números de Bernoulli:
En esencia, todos estos resultados son valores de la función zeta de Riemann para valores negativos de la misma, o sea:
Otras consecuencias
Recientemente, el uso de C(1) ha sido propuesto como sumatorio de Ramanujan, puesto que se puede asegurar que una serie  admite una y sólo una sumatoria de Ramanujan, definida como el valor en 1 de la única solución de la ecuación en diferencias
admite una y sólo una sumatoria de Ramanujan, definida como el valor en 1 de la única solución de la ecuación en diferencias 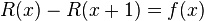 que verifica la condición
que verifica la condición 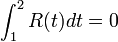 .2
.2
 admite una y sólo una sumatoria de Ramanujan, definida como el valor en 1 de la única solución de la ecuación en diferencias
admite una y sólo una sumatoria de Ramanujan, definida como el valor en 1 de la única solución de la ecuación en diferencias 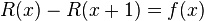 que verifica la condición
que verifica la condición 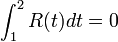 .2
.2
La nueva definición de sumatorio de Ramanujan (denotado  ) no coincide con la anterior definición de sumatorio de Ramanujan (C(0)) ni con la suma de series convergentes, pero tiene propiedades interesantes, tales como: Si R(x) tiende a un límite finito cuando x→1, entonces la serie
) no coincide con la anterior definición de sumatorio de Ramanujan (C(0)) ni con la suma de series convergentes, pero tiene propiedades interesantes, tales como: Si R(x) tiende a un límite finito cuando x→1, entonces la serie  es convergente, obteniéndose:
es convergente, obteniéndose:
 ) no coincide con la anterior definición de sumatorio de Ramanujan (C(0)) ni con la suma de series convergentes, pero tiene propiedades interesantes, tales como: Si R(x) tiende a un límite finito cuando x→1, entonces la serie
) no coincide con la anterior definición de sumatorio de Ramanujan (C(0)) ni con la suma de series convergentes, pero tiene propiedades interesantes, tales como: Si R(x) tiende a un límite finito cuando x→1, entonces la serie  es convergente, obteniéndose:
es convergente, obteniéndose:
Otro interesante resultado es el siguiente:
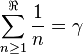 ,
,
donde  es la constante de Euler-Mascheroni.
es la constante de Euler-Mascheroni.
 es la constante de Euler-Mascheroni.
es la constante de Euler-Mascheroni.
superaditiva si satisface la siguiente inecuación para todo valor de m y n:

Lema de Fekete
El siguiente lema de Michael Fakete justifica en gran parte la utilización de secuencias superaditivas.Para cada secuencia superaditiva {an}, n ≥ 1, el límite: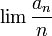 existe y es igual a sup an/n.
existe y es igual a sup an/n.
Este límite puede ser infinito, por ejemplo, para la secuencia an = log n!.Superaditividad en funciones
Análogamente, una función f(x) es superaditiva sipara todo x e y en el dominio de f.Por ejemplo,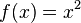 es una función superaditiva para números reales no negativos, porque en tal caso el cuadrado de
es una función superaditiva para números reales no negativos, porque en tal caso el cuadrado de  es siempre mayor que la suma de los cuadrados de
es siempre mayor que la suma de los cuadrados de  e
e  .Horst Alzer demostró1 que la Función gamma de Hadamard H(x) es superaditiva para números reales x, y mayores que 1.5031.El Lema de Fekete es aplicable también a funciones subaditivas. Existen extensiones de este Lema que no requieren la definición de superaditividad. Existen también resultados que permiten deducir el ratio de convergencia para el límite cuya existencia está establecido en el Lemma de Fakete. Una buena exposición de este tópico puede encontrarse en Steele (1997).2Si f es una función superaditiva, y si 0 está en su dominio, entonces f(0) ≤ 0. Para corroborar esto, considere la inecuación superior:
.Horst Alzer demostró1 que la Función gamma de Hadamard H(x) es superaditiva para números reales x, y mayores que 1.5031.El Lema de Fekete es aplicable también a funciones subaditivas. Existen extensiones de este Lema que no requieren la definición de superaditividad. Existen también resultados que permiten deducir el ratio de convergencia para el límite cuya existencia está establecido en el Lemma de Fakete. Una buena exposición de este tópico puede encontrarse en Steele (1997).2Si f es una función superaditiva, y si 0 está en su dominio, entonces f(0) ≤ 0. Para corroborar esto, considere la inecuación superior: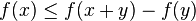 , y por lo tanto
, y por lo tanto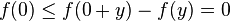
El negativo de una función superaditiva es subaditiva.- supremo de S, si existe, es el mínimo elemento de P que es mayor o igual a cada elemento de S. En otras palabras, es la mínima de las cotas superiores de S. El supremo de un conjunto S comúnmente se denota sup(S).
Definiciones
Sea T un subconjunto de R.- Si T está acotado por arriba , entonces se dice que una cota superior es un supremo - o una mínima cota superior- de T si es menor que cualquier cota superior de T.
- Si T está acotado por abajo, entonces se dice que una cota inferior es un ínfimo - o una máxima cota inferior- de T si es mayor que cualquier cota inferior de T.1
Propiedades
- s es supremo del subconjunto T no vacío del conjunto R de números reales si es cota superior de T y si sólo si para toda ε > 0 existe sε en T tal que s-ε < sε.
- r es ínfimo del subconjunto T no vacío del conjunto R de números reales si es cota inferior de T y si sólo si para toda ε > 0 existe rε en T tal que r+ε > sε.
- Sea L un subconjunto acotado de números reales. A su vez K un subconjunto no vacío de L, entonces se cumple que inf L ≤ inf K ≤ sup K ≤inf L. 2
- Si el supremo existe, entonces es único
 , si es que dichos supremos existen
, si es que dichos supremos existen- Un conjunto tiene máximo, si y solo si el supremo es elemento de dicho conjunto.
Ejemplos
- En el campo de los números reales, todo subconjunto no vacío, acotado superiormente posee un supremo, contenido o no dentro del subconjunto.
- teorema de inversión de Lagrange, también denominado fórmula de Lagrange-Bürmann , permite obtener la expansión enserie de Taylor de la función inversa de una función analítica.
Enunciado del teorema
Si la dependencia entre las variables w y z se encuentra definida de forma implícita mediante una ecuación del tipodonde f es analítica en un punto a y f '(a) ≠ 0. Entonces es posible invertir o resolver la ecuación para w:donde g es analítica en el punto b = f(a). Esto es también denominado reversión de series.La expansión en serie de g esEsta fórmula también vale para series de potencia formales y puede ser generalizada de varias maneras. Puede ser formulada para funciones de varias variables, puede ser extendida para cubrir el caso F(g(z)) para una función analítica F, y puede ser generalizada para el caso f '(a) = 0, donde la inversa g es una función multivaluada.El teorema fue demostrado por Lagrange1 y generalizado por Hans Heinrich Bürmann,2 3 4 ambos a finales del siglo XVIII. Existe una deducción directa utilizandoanálisis complejo e integración de contorno; la versión de series complejas de potencia formales es claramente una consecuencia de conocer la fórmula de polinomios, de forma que se pueda aplicar la teoría de funciones analíticas. En realidad, la maquinaria de la teoría de funciones analíticas solo entra en un punto formal en esta demostración, lo que hace falta es alguna propiedad del residuo formal, y existe una demostración formal directa.


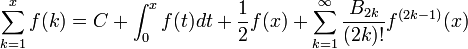

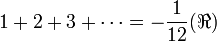
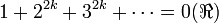



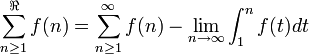


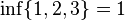
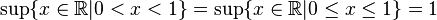








No hay comentarios:
Publicar un comentario