El argumento de la diagonal de Cantor, también conocido como método de la diagonal, es una argumentación o demostración matemática vislumbrada por Georg Cantor hacia 1891 para demostrar que el conjunto de los números realesno es numerable.
Esta demostración de la imposibilidad de contar o enumerar los números reales no fue la primera, pero sí la más sencilla y elegante. Posteriormente, esta demostración inspiró otras demostraciones, conocidas como argumento diagonal por la analogía con esta demostración.
Números reales
La prueba original de Cantor demuestra que el intervalo [0,1] no es numerable, es decir, no podemos enumerar la lista de todos los reales dentro del intervalo (siempre habrá más). Se extiende a todos los reales, ya que es posible equipotenciar estos al intervalo. Podemos demostrar que lo que es válido para el intervalo [0,1] lo es para cualquier otro, por grande que sea (exceptuando el intervalo [0,0] que tiene un solo valor el cero).
La demostración es por reducción al absurdo:
- Se supone que el intervalo [0,1] es infinito numerable.
- En ese caso se podría elaborar una secuencia de los números, ( r1, r2, r3,... )
- Se sabe que los reales entre 0 y 1 pueden ser representados solamente escribiendo sus decimales.
- Se colocan los números en la lista (no necesariamente en orden). Considerando los decimales periódicos, como 0.499... = 0.500..., como los que tienen infinitos nueves.
La secuencia podría tener un aspecto similar a:
- r1 = 0. 5 1 0 5 1 1 0...
- r2 = 0. 4 1 3 2 0 4 3...
- r3 = 0. 8 2 4 5 0 2 6...
- r4 = 0. 2 3 3 0 1 2 6...
- r5 = 0. 4 1 0 7 2 4 6...
- r6 = 0. 9 9 3 7 8 3 8...
- r7 = 0. 0 1 0 5 1 3 5...
- ...
Dada la primera premisa dicha lista contiene todos los números reales entre 0 y 1. Con esto, se puede construir un número x que debería estar en la lista. Para eso usamos los números de la diagonal.
- r1 = 0. 5 1 0 5 1 1 0...
- r2 = 0. 4 1 3 2 0 4 3...
- r3 = 0. 8 2 4 5 0 2 6...
- r4 = 0. 2 3 3 0 1 2 6...
- r5 = 0. 4 1 0 7 2 4 6...
- r6 = 0. 9 9 3 7 8 3 8...
- r7 = 0. 0 1 0 5 1 3 5...
- ...
- El número x está definido así: al dígito xk le corresponde el (k+1)ésimo dígito de rk (en caso de que fuera un nueve, se le asigna el dígito cero)
Entonces x= 0.6251346.... El número x es claramente un real. Pero... ¿Dónde está x?
Si yo quisiera decir que x está en el enésimo lugar de mi lista, no sería cierto, ya que el enésimo dígito de rn es distinto al de x.
- Entonces ésta no es una lista completa de los reales en el intervalo [0,1].
- Existe una contradicción, que nace de la premisa de suponer que estos números son infinitos numerables.
Para extender este resultado al campo R tenemos que establecer una relación biyectiva entre este intervalo y los reales. Esto es posible gracias a una función como ésta:
Con esto podemos decir que hay tantos números reales como reales hay entre 0 y 1.
Numeros enteros positivos
El argumento de la diagonal de Cantor está íntimamente ligado al Teorema de Cantor. La relación entre ambos puede entenderse en términos de la numerabilidad de un conjunto. Un conjunto se dice numerable o contable si existe una relación biyectiva entre los elementos del conjunto y los números enteros positivos; esto es, si es posible organizar a los elementos del conjunto de tal manera que todos los elementos del conjunto aparecen antes o después, incluso repetidas veces, en la lista. En tal caso, los elementos del conjunto pueden ser asignados un 'marcador' o 'índice', que sería el correspondiente número entero positivo (esto es, al primer elemento de la lista le sería asignada la etiqueta 1; al segundo, 2;etc). Como quiera que esto es posible en tanto en cuanto el conjunto sea numerable, operar con los elemntos del conjunto, o con sus etiquetas es equivalente.
El argumento de la diagonal de Cantor establece que
|
Demostración
Sea P el conjunto de todos los conjuntos de números enteros positivos. Sea L una lista infinita cualquiera de conjuntos de enteros positivos:
donde  son conjuntos cualesquiera de enteros positivos. Si el conjunto P fuera numerable, entonces sería posible definir una lista L tal que incluya a todos los conjuntos de números enteros positivos. Sin embargo, el argumento de diagonalización demuestra que esto no es posible.
son conjuntos cualesquiera de enteros positivos. Si el conjunto P fuera numerable, entonces sería posible definir una lista L tal que incluya a todos los conjuntos de números enteros positivos. Sin embargo, el argumento de diagonalización demuestra que esto no es posible.
 son conjuntos cualesquiera de enteros positivos. Si el conjunto P fuera numerable, entonces sería posible definir una lista L tal que incluya a todos los conjuntos de números enteros positivos. Sin embargo, el argumento de diagonalización demuestra que esto no es posible.
son conjuntos cualesquiera de enteros positivos. Si el conjunto P fuera numerable, entonces sería posible definir una lista L tal que incluya a todos los conjuntos de números enteros positivos. Sin embargo, el argumento de diagonalización demuestra que esto no es posible.
Sea  un conjunto de números enteros positivos definido como sigue:
un conjunto de números enteros positivos definido como sigue:
 un conjunto de números enteros positivos definido como sigue:
un conjunto de números enteros positivos definido como sigue:
donde  es el conjunto de números enteros positivos. Esto indica que
es el conjunto de números enteros positivos. Esto indica que  está formado por todos aquellos enteros positivos n tales que al mismo tiempo no formen parte del conjunto
está formado por todos aquellos enteros positivos n tales que al mismo tiempo no formen parte del conjunto  de la lista L. Por tanto, la composición de
de la lista L. Por tanto, la composición de  depende de la composición de la lista L. Es fácil ver que
depende de la composición de la lista L. Es fácil ver que  existe: supóngase por ejemplo que
existe: supóngase por ejemplo que es el conjunto de todos los números positivos impares. Entonces,
es el conjunto de todos los números positivos impares. Entonces, 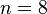 no pertenece a
no pertenece a  , y por tanto pertenece a
, y por tanto pertenece a  .
.
 es el conjunto de números enteros positivos. Esto indica que
es el conjunto de números enteros positivos. Esto indica que  está formado por todos aquellos enteros positivos n tales que al mismo tiempo no formen parte del conjunto
está formado por todos aquellos enteros positivos n tales que al mismo tiempo no formen parte del conjunto  de la lista L. Por tanto, la composición de
de la lista L. Por tanto, la composición de  depende de la composición de la lista L. Es fácil ver que
depende de la composición de la lista L. Es fácil ver que  existe: supóngase por ejemplo que
existe: supóngase por ejemplo que es el conjunto de todos los números positivos impares. Entonces,
es el conjunto de todos los números positivos impares. Entonces, 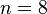 no pertenece a
no pertenece a  , y por tanto pertenece a
, y por tanto pertenece a  .
.
Si P fuera enumerable, entonces debería existir una lista L tal que  formara parte de ella como elemento
formara parte de ella como elemento  . En cuyo caso, se seguiría que
. En cuyo caso, se seguiría que
 formara parte de ella como elemento
formara parte de ella como elemento  . En cuyo caso, se seguiría que
. En cuyo caso, se seguiría que
Esto implica una contradicción, pues cuando  , ocurre que
, ocurre que  , esto es,
, esto es,  debería formar y no formar parte de
debería formar y no formar parte de  al mismo tiempo.
al mismo tiempo.
 , ocurre que
, ocurre que  , esto es,
, esto es,  debería formar y no formar parte de
debería formar y no formar parte de  al mismo tiempo.
al mismo tiempo.
Por tanto, no es posible construir una lista L tal que contenga al menos una vez a todos los elementos del conjunto de todos los conjuntos de números enteros positivos. O, dicho de otro modo, el conjunto P de todos los conjuntos de enteros positivos no es numerable.
aridad de un operador matemático o de una función es el número de argumentos necesarios para que dicho operador o función se pueda calcular.
Por ejemplo, el operador de suma «+» es un operador binario (de aridad 2), porque necesita dos argumentos para poder realizar una suma. En cambio, la función valor absoluto «| |» es un operador unario (de aridad 1), porque sólo necesita un argumento.
El término también es utilizado en lógica matemática para referir relaciones, por ejemplo relación n-aria.
operación binaria (o ley de composición)1 aquella operación matemática, que necesita el operador y dos operandos (argumentos) para que se pueda calcular un valor.
Dados tres conjuntos A, B y C una operación binaria producto, representando la operación por el signo  , es una aplicación que asigna a cada par de valores a de A y bde B un solo valor c de C, que podemos representar:
, es una aplicación que asigna a cada par de valores a de A y bde B un solo valor c de C, que podemos representar:
 , es una aplicación que asigna a cada par de valores a de A y bde B un solo valor c de C, que podemos representar:
, es una aplicación que asigna a cada par de valores a de A y bde B un solo valor c de C, que podemos representar:
Podemos expresar la operación:
Por ejemplo, el operador de suma «+» de números naturales es un operador binario, porque requiere dos argumentos:
y tenemos que:
El número de argumentos de una función se denomina aridad.
Clase de operación binaria
Según los conjuntos A, B y C podemos diferenciar dos tipos de operaciones, las internas en las que A = B = C, y las externas que son todas las demás, se denomina Ley de composición a un subtipo de operación binaria.
Operación interna
Si a cada par de valores (a, b) de 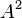 la operación le corresponde un valor c de A:
la operación le corresponde un valor c de A:
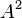 la operación le corresponde un valor c de A:
la operación le corresponde un valor c de A:
se dice que esta operación es interna, también se llama ley de composición interna, así por ejemplo dado el conjunto de vectores de tres dimensiones  y la adición de vectores, se tiene:
y la adición de vectores, se tiene:
 y la adición de vectores, se tiene:
y la adición de vectores, se tiene:
que la suma de dos vectores de  es otro vector de
es otro vector de  , por ejemplo, dados los vectores:
, por ejemplo, dados los vectores:
 es otro vector de
es otro vector de  , por ejemplo, dados los vectores:
, por ejemplo, dados los vectores:
su suma es:
Operación externa
Si la operación no es interna entonces es externa, pudiéndose presentar los siguientes casos:
- Si a cada par de valores a de A y b de B, se le asigna un valor c de A,
a esta operación también se denomina ley de composición externa, un ejemplo claro, de esta operación, es el producto de un vector por un escalar:
así, dado el vector:
el resultado de multiplicarlo por un escalar b, será:
- Si la operación es de la forma:
en la que a cada par de valores a, b de A se le asigna un c de B, esta operación no se denomina ley de composición, como ejemplo podemos poner el producto escalar de dos vectores, que da como resultado un número real:
así dados los vectores:
su producto escalar será:
- Si la operación asigna a cada par de valores a de A y b de B un c de C, siendo A, B y C conjuntos distintos:
es el caso más general, y tampoco se denomina ley de composición, podemos ver el ejemplo de la división de un número entero entre un número natural para dar como resultado un número racional
![\begin{array}{rccl}
f : & (0,1) & \to & \mathbb{R} \\
& x & \to & y = f(x) = \tan\left[\pi\left(x-\frac{1}{2}\right)\right]
\end{array}](https://upload.wikimedia.org/math/2/f/4/2f4a5a0f07d0f60b89eaed5fedc37623.png)
























No hay comentarios:
Publicar un comentario