bola, en topología y otras ramas de matemática, es el conjunto de puntos que distan de otro igual o menos que una distancia dada, llamada radio. Es un concepto fundamental en el Análisis Matemático. Se distinguen dos tipos: las abiertas y las cerradas.
Bola abierta
Una bola abierta, en topología, es el conjunto de puntos que distan de otro punto (el centro), a una distancia menor a la determinada (el radio). Equivale al conjunto de puntos contenidos dentro de una superficie esférica, excluida dicha superficie.
Definición y notaciones
Sea  un espacio pseudométrico (por lo general se toma un espacio métrico, pero basta con que
un espacio pseudométrico (por lo general se toma un espacio métrico, pero basta con que  sea pseudodistancia). Sea un número real
sea pseudodistancia). Sea un número real 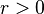 . Sea
. Sea  . Se define la bola abierta de centro
. Se define la bola abierta de centro  y radio
y radio  (o simplemente bola de centro
(o simplemente bola de centro  y radio
y radio  ) como el conjunto
) como el conjunto  .
.
 un espacio pseudométrico (por lo general se toma un espacio métrico, pero basta con que
un espacio pseudométrico (por lo general se toma un espacio métrico, pero basta con que  sea pseudodistancia). Sea un número real
sea pseudodistancia). Sea un número real 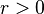 . Sea
. Sea  . Se define la bola abierta de centro
. Se define la bola abierta de centro  y radio
y radio  (o simplemente bola de centro
(o simplemente bola de centro  y radio
y radio  ) como el conjunto
) como el conjunto  .
.
Este conjunto tiene distintas maneras de denotarse. La usual y universal es  . A veces, si en el espacio existen distintas (pseudo-)distancias definidas, se hace hincapié en qué (pseudo)-distancia se está usando para definir el conjunto, utilizando esta notación:
. A veces, si en el espacio existen distintas (pseudo-)distancias definidas, se hace hincapié en qué (pseudo)-distancia se está usando para definir el conjunto, utilizando esta notación:  . En algunos textos se denota sin embargo por
. En algunos textos se denota sin embargo por  .
.
 . A veces, si en el espacio existen distintas (pseudo-)distancias definidas, se hace hincapié en qué (pseudo)-distancia se está usando para definir el conjunto, utilizando esta notación:
. A veces, si en el espacio existen distintas (pseudo-)distancias definidas, se hace hincapié en qué (pseudo)-distancia se está usando para definir el conjunto, utilizando esta notación:  . En algunos textos se denota sin embargo por
. En algunos textos se denota sin embargo por  .
.
En Análisis Funcional, cuando se trabaja con espacios normados se prefiere la notación  para denotar la bola abierta. Así,
para denotar la bola abierta. Así,  denota a la bola de centro
denota a la bola de centro  y radio
y radio  . La notación
. La notación  se reserva para las bolas cerradas (con el peligro de confusión que eso genera).
se reserva para las bolas cerradas (con el peligro de confusión que eso genera).
 para denotar la bola abierta. Así,
para denotar la bola abierta. Así,  denota a la bola de centro
denota a la bola de centro  y radio
y radio  . La notación
. La notación  se reserva para las bolas cerradas (con el peligro de confusión que eso genera).
se reserva para las bolas cerradas (con el peligro de confusión que eso genera).
Cuando hablamos de espacios euclídeos, la bola es "redonda", en el sentido intuitivo del término, por lo que la bola de centro  y radio
y radio  coincide en esos casos con los puntos encerrados en el interior de una superficie esférica. En el caso particular del plano, la figura entonces obtenida (es decir, el conjunto
coincide en esos casos con los puntos encerrados en el interior de una superficie esférica. En el caso particular del plano, la figura entonces obtenida (es decir, el conjunto  ) es el disco (abierto) de centro
) es el disco (abierto) de centro  y radio
y radio  , razón por la cual se denota por
, razón por la cual se denota por  . Nótese que esta situación se da en particular en Variable Compleja, siendo entonces la notación
. Nótese que esta situación se da en particular en Variable Compleja, siendo entonces la notación  (donde
(donde  representa el módulo de
representa el módulo de  ). Aunque no es estándar, sí es usual encontrar textos en los que
). Aunque no es estándar, sí es usual encontrar textos en los que  denota al disco de radio unidad centrado en el origen, i.e.,
denota al disco de radio unidad centrado en el origen, i.e.,  .
.
 y radio
y radio  coincide en esos casos con los puntos encerrados en el interior de una superficie esférica. En el caso particular del plano, la figura entonces obtenida (es decir, el conjunto
coincide en esos casos con los puntos encerrados en el interior de una superficie esférica. En el caso particular del plano, la figura entonces obtenida (es decir, el conjunto  ) es el disco (abierto) de centro
) es el disco (abierto) de centro  y radio
y radio  , razón por la cual se denota por
, razón por la cual se denota por  . Nótese que esta situación se da en particular en Variable Compleja, siendo entonces la notación
. Nótese que esta situación se da en particular en Variable Compleja, siendo entonces la notación  (donde
(donde  representa el módulo de
representa el módulo de  ). Aunque no es estándar, sí es usual encontrar textos en los que
). Aunque no es estándar, sí es usual encontrar textos en los que  denota al disco de radio unidad centrado en el origen, i.e.,
denota al disco de radio unidad centrado en el origen, i.e.,  .
.Propiedades
Toda bola abierta es un conjunto abierto.
El conjunto de todas las bolas abiertas de un espacio pseudométrico ( ) forman una base de la topología asociada a la pseudodistancia. Si consideramos un punto cualquiera del espacio y lo fijamos (por ejemplo, el punto
) forman una base de la topología asociada a la pseudodistancia. Si consideramos un punto cualquiera del espacio y lo fijamos (por ejemplo, el punto  ), el conjunto de bolas abiertas centradas en
), el conjunto de bolas abiertas centradas en  (
( ) forman unabase de entornos de
) forman unabase de entornos de  . En concreto es una base de entornos abiertos, conexos, conexos por caminos y simplemente conexos. Si el espacio es además un espacio vectorial topológico, también es base de entornos convexos. De hecho, podemos tomar la siguiente base de entornos:
. En concreto es una base de entornos abiertos, conexos, conexos por caminos y simplemente conexos. Si el espacio es además un espacio vectorial topológico, también es base de entornos convexos. De hecho, podemos tomar la siguiente base de entornos:  que (además de tener todas las propiedades antedichas) es numerable. Esto prueba que todo espacio pseudométrico cumple el Primer Axioma de Numerabilidad.
que (además de tener todas las propiedades antedichas) es numerable. Esto prueba que todo espacio pseudométrico cumple el Primer Axioma de Numerabilidad.
 ) forman una base de la topología asociada a la pseudodistancia. Si consideramos un punto cualquiera del espacio y lo fijamos (por ejemplo, el punto
) forman una base de la topología asociada a la pseudodistancia. Si consideramos un punto cualquiera del espacio y lo fijamos (por ejemplo, el punto  ), el conjunto de bolas abiertas centradas en
), el conjunto de bolas abiertas centradas en  (
( ) forman unabase de entornos de
) forman unabase de entornos de  . En concreto es una base de entornos abiertos, conexos, conexos por caminos y simplemente conexos. Si el espacio es además un espacio vectorial topológico, también es base de entornos convexos. De hecho, podemos tomar la siguiente base de entornos:
. En concreto es una base de entornos abiertos, conexos, conexos por caminos y simplemente conexos. Si el espacio es además un espacio vectorial topológico, también es base de entornos convexos. De hecho, podemos tomar la siguiente base de entornos:  que (además de tener todas las propiedades antedichas) es numerable. Esto prueba que todo espacio pseudométrico cumple el Primer Axioma de Numerabilidad.
que (además de tener todas las propiedades antedichas) es numerable. Esto prueba que todo espacio pseudométrico cumple el Primer Axioma de Numerabilidad.
Si el espacio es un espacio normado, toda bola abierta es homeomorfa al espacio.
En matemática (en concreto en topología y en las ramas que la utilizan), una bola cerrada es un conjunto de puntos que distan de otro no más que un cierto radio. Es un concepto fundamental en el Análisis Matemático.
Bola cerrada
Una bola cerrada, en topología, es el conjunto de puntos que distan de otro (el centro), una distancia igual o menor dada (el radio). Equivale al conjunto de puntos contenidos dentro de una superficie esférica, incluida dicha superficie.
Definición y notaciones
Sea  un espacio pseudométrico (por lo general se toma un espacio métrico, pero basta con que
un espacio pseudométrico (por lo general se toma un espacio métrico, pero basta con que  sea pseudodistancia). Sea un número real
sea pseudodistancia). Sea un número real 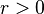 . Sea
. Sea  . Se define la bola cerrada de centro
. Se define la bola cerrada de centro  y radio
y radio  como el conjunto
como el conjunto  .
.
 un espacio pseudométrico (por lo general se toma un espacio métrico, pero basta con que
un espacio pseudométrico (por lo general se toma un espacio métrico, pero basta con que  sea pseudodistancia). Sea un número real
sea pseudodistancia). Sea un número real 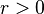 . Sea
. Sea  . Se define la bola cerrada de centro
. Se define la bola cerrada de centro  y radio
y radio  como el conjunto
como el conjunto  .
.
Este conjunto tiene distintas maneras de denotarse. La usual y universal es  , o también
, o también  . A veces, si en el espacio existen distintas (pseudo-)distancias definidas, se hace hincapié en qué (pseudo)-distancia se está usando para definir el conjunto, utilizando esta notación:
. A veces, si en el espacio existen distintas (pseudo-)distancias definidas, se hace hincapié en qué (pseudo)-distancia se está usando para definir el conjunto, utilizando esta notación:  . En algunos textos se denota sin embargo por
. En algunos textos se denota sin embargo por  .
.
 , o también
, o también  . A veces, si en el espacio existen distintas (pseudo-)distancias definidas, se hace hincapié en qué (pseudo)-distancia se está usando para definir el conjunto, utilizando esta notación:
. A veces, si en el espacio existen distintas (pseudo-)distancias definidas, se hace hincapié en qué (pseudo)-distancia se está usando para definir el conjunto, utilizando esta notación:  . En algunos textos se denota sin embargo por
. En algunos textos se denota sin embargo por  .
.
En Análisis Funcional, cuando se trabaja con espacios normados la notación  se reserva para las bolas cerradas, usando para las bolas abiertas la notación
se reserva para las bolas cerradas, usando para las bolas abiertas la notación  (con el peligro de confusión que eso genera).
(con el peligro de confusión que eso genera).
 se reserva para las bolas cerradas, usando para las bolas abiertas la notación
se reserva para las bolas cerradas, usando para las bolas abiertas la notación  (con el peligro de confusión que eso genera).
(con el peligro de confusión que eso genera).
Cuando hablamos de espacios euclídeos, la bola es "redonda", en el sentido intuitivo del término, por lo que la bola de centro  y radio
y radio  coincide en esos casos con los puntos encerrados por una superficie esférica (entendiendo que consideramos los puntos de la propia superficie esférica como puntos de la bola). En el caso particular del plano, la figura entonces obtenida (es decir, el conjunto
coincide en esos casos con los puntos encerrados por una superficie esférica (entendiendo que consideramos los puntos de la propia superficie esférica como puntos de la bola). En el caso particular del plano, la figura entonces obtenida (es decir, el conjunto  ) es el disco cerrado de centro
) es el disco cerrado de centro  y radio
y radio  , razón por la cual se denota por
, razón por la cual se denota por  . Nótese que esta situación se da en particular en Variable Compleja, siendo entonces la notación
. Nótese que esta situación se da en particular en Variable Compleja, siendo entonces la notación  (donde
(donde  representa el módulo de
representa el módulo de  ). Aunque no es estándar, sí es usual encontrar textos en los que
). Aunque no es estándar, sí es usual encontrar textos en los que  denota al disco de radio unidad centrado en el origen, i.e.,
denota al disco de radio unidad centrado en el origen, i.e.,  .
.
 y radio
y radio  coincide en esos casos con los puntos encerrados por una superficie esférica (entendiendo que consideramos los puntos de la propia superficie esférica como puntos de la bola). En el caso particular del plano, la figura entonces obtenida (es decir, el conjunto
coincide en esos casos con los puntos encerrados por una superficie esférica (entendiendo que consideramos los puntos de la propia superficie esférica como puntos de la bola). En el caso particular del plano, la figura entonces obtenida (es decir, el conjunto  ) es el disco cerrado de centro
) es el disco cerrado de centro  y radio
y radio  , razón por la cual se denota por
, razón por la cual se denota por  . Nótese que esta situación se da en particular en Variable Compleja, siendo entonces la notación
. Nótese que esta situación se da en particular en Variable Compleja, siendo entonces la notación  (donde
(donde  representa el módulo de
representa el módulo de  ). Aunque no es estándar, sí es usual encontrar textos en los que
). Aunque no es estándar, sí es usual encontrar textos en los que  denota al disco de radio unidad centrado en el origen, i.e.,
denota al disco de radio unidad centrado en el origen, i.e.,  .
.Propiedades
Toda bola cerrada es un conjunto cerrado.
El conjunto de todas las bolas cerradas de un espacio seudométrico ( ) no forman una base de los cerrados de la topología asociada a la seudodistancia.Sin embargo, si consideramos un punto cualquiera del espacio y lo fijamos (por ejemplo, el punto
) no forman una base de los cerrados de la topología asociada a la seudodistancia.Sin embargo, si consideramos un punto cualquiera del espacio y lo fijamos (por ejemplo, el punto  ), el conjunto de bolas cerradas centradas en
), el conjunto de bolas cerradas centradas en  (
( ) forman una base de entornos de
) forman una base de entornos de  . En concreto es una base de entornos cerrados, compactos, conexos, conexos por caminos y simplemente conexos. Si el espacio es además un espacio vectorial topológico, también es base de entornos convexos. De hecho, podemos tomar la siguiente base de entornos:
. En concreto es una base de entornos cerrados, compactos, conexos, conexos por caminos y simplemente conexos. Si el espacio es además un espacio vectorial topológico, también es base de entornos convexos. De hecho, podemos tomar la siguiente base de entornos:  que (además de tener todas las propiedades antedichas) es numerable. Esto prueba que todo espacio seudométrico cumple el Primer Axioma de Numerabilidad.
que (además de tener todas las propiedades antedichas) es numerable. Esto prueba que todo espacio seudométrico cumple el Primer Axioma de Numerabilidad.
 ) no forman una base de los cerrados de la topología asociada a la seudodistancia.Sin embargo, si consideramos un punto cualquiera del espacio y lo fijamos (por ejemplo, el punto
) no forman una base de los cerrados de la topología asociada a la seudodistancia.Sin embargo, si consideramos un punto cualquiera del espacio y lo fijamos (por ejemplo, el punto  ), el conjunto de bolas cerradas centradas en
), el conjunto de bolas cerradas centradas en  (
( ) forman una base de entornos de
) forman una base de entornos de  . En concreto es una base de entornos cerrados, compactos, conexos, conexos por caminos y simplemente conexos. Si el espacio es además un espacio vectorial topológico, también es base de entornos convexos. De hecho, podemos tomar la siguiente base de entornos:
. En concreto es una base de entornos cerrados, compactos, conexos, conexos por caminos y simplemente conexos. Si el espacio es además un espacio vectorial topológico, también es base de entornos convexos. De hecho, podemos tomar la siguiente base de entornos:  que (además de tener todas las propiedades antedichas) es numerable. Esto prueba que todo espacio seudométrico cumple el Primer Axioma de Numerabilidad.
que (además de tener todas las propiedades antedichas) es numerable. Esto prueba que todo espacio seudométrico cumple el Primer Axioma de Numerabilidad.Bola abierta
Descripción:
Dados a∈Rn y r>0 la bola abierta de centro a y de radio r , se simboliza por B(a,r) y se define como B(a,r)=:{x∈Rn/d(x,a)<r}
Descriptores:
Topología
Álgebra
Ejemplo:
El intervalo abierto ]3,5[⊂R es una bola abierta de centro 4 y radio 1, ]3,5[={x∈R/3<x<5}
El conjuntoB((2,0);3) de R2 , dado por: B((2,0);3)={(x,y)∈R2/(x−2)2+y2<9} es una bola abierta en R2
Bola cerrada
Descripción:
Dados a∈Rn y r>0 la bola cerrada de centro a y de radio r , se simboliza por B¯(a,r) y se define como B¯(a,r)=:{x∈Rn/d(x,a)≤r}
Descriptores:
Topología
Álgebra
Ejemplo:
El intervalo cerrado [3,5]⊂R es una bola cerrada de centro 4 y radio 1, [3,5]={x∈R/3≤x≤5}
El conjuntoB−((2,0);3) de R2 , dado por: B−((2,0);3)={(x,y)∈R2/(x−2)2+y2≤9} es una bola cerrada en R2
cambio de variable es una técnica empleada en matemática para resolver algunas ecuaciones o sistemas de ecuaciones de grado superior a uno, que de otra forma sería más complejo resolver. Mediante este sistema se da paso a una ecuación equivalente, y, una vez resuelta, se deshace el cambio para obtener el valor de la incógnitainicial. Se emplea en los siguientes casos:
- Ecuaciones bicuadradas
- Ecuaciones y sistemas exponenciales
- Ecuaciones de tercer grado
- Ecuaciones de cuarto grado
Ejemplo: resolución de una ecuación exponencial mediante cambio de variable:
Existen tres tipos de ecuaciones exponenciales; en el segundo caso pueden reducirse a una de segundo grado. Es el caso de  . Se siguen los siguientes pasos:
. Se siguen los siguientes pasos:
 . Se siguen los siguientes pasos:
. Se siguen los siguientes pasos:- Se factoriza 9 en 32 para que tenga la misma base que 7 · 3x:
- Se realiza el cambio de variable 3x = z, por lo que 32x = z2, y tenemos:
- Se deshace el cambio de variable:
La única solución es x = 2, ya que las potencias de 3 siempre son positivas, por lo que 3x = - 2 no puede cumplirse.
Resolución de Integrales por Cambio de Variable
Consiste en igualar una parte del integrando a una nueva variable, por ejemplo u, llamada variable auxiliar. Luego de esto, se debe calcular la derivada de la variable auxiliar y realizar las operaciones necesarias, para que ni en el integrando ni en el diferencial, aparezca alguna expresión en términos de la variable original. A esto se le denomina cambio de variable (CDV).
Luego de hacer efectivo el CDV, por lo general, se obtienen integrales más sencillas que la original, las cuales se resuelven aplicando lo aprendido en el método anterior. Por esta razón, es necesario que el lector haya estudiado detalladamente dicho método puesto que en la solución de los ejemplos de esta parte de la obra, no se incluye una explicación específica de este contenido que ya debe ser parte de sus redes conceptuales.
Es importante señalar que el resultado de la integración, debe estar en función de las variables originales por lo que se acostumbra a emplear el término “devolviendo el cambio de variable” para reseñar el proceso mediante el cual la variable auxiliar desaparece de la respuesta definitiva.
Resolver la siguiente integral: | |||
Solución
| |||
| |||
v En atención a la teoría expuesta, construir la siguiente igualdad:
u= 2x+6 (1)
v Debido a (1), la integral original se transforma, momentáneamente en:
v Como la integral a resolver no debe quedar en función de la variable original, se debe expresar adx, en función de du y para ello se:
· Deriva ambos miembros de (1) para obtener:
du=2dx
· Divide la expresión anterior entre 2, obteniéndose:
v Si en (2), se reemplaza a dx por la expresión obtenida en (3) y además se aplica la propiedad 1de los O.L , se obtiene:
v Efectuado el CDV se obtiene una integral inmediata. Para su solución basta con aplicar laEcuación 1.1. Así:
v Devolviendo el CDV, u=2x+6 , se obtiene la respuesta final. Por tanto:
| |||
Ejemplo 2
| ||||||||||||||||||||||||||||||||||||
Solución
| ||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||
v En atención a la teoría expuesta, construir la siguiente igualdad:
u= 4x -1 (1)
v Debido a (1), la integral original se transforma, momentáneamente en:
v Como la integral a resolver no debe quedar en función de la variable original, se debe expresar adx, en función de du y para ello se:
· Deriva ambos miembros de (1) para obtener:
du=4dx
· Divide la expresión anterior entre 4, obteniéndose:
v Si en (2), se reemplaza a dx por la expresión obtenida en (3) y además se aplica la propiedad 1de los O.L , se obtiene:
v Efectuado el CDV se obtiene una integral inmediata. Aplicando exponente fraccionario y laEcuación 1.1., se obtiene:
v Devolviendo el CDV, u= 4x -1, se obtiene la respuesta final. Por tanto:
| ||||||||||||||||||||||||||||||||||||



No hay comentarios:
Publicar un comentario