Algoritmos criptográficos
El sistema de compartición de secretos de Shamir es un algoritmo criptográfico. Es una forma de compartición de secretos donde un secreto se divide en partes y se da a cada participante una sola: todas o parte de ellas son necesarias para reconstruir el secreto.
El algoritmo basa su funcionamiento en una propiedad de los polinomios interpoladores1 y fue desarrollado por el criptógrafoisraelí Adi Shamir, que lo presentó en 1979.
Definición matemática
Formalmente, nuestro objetivo es dividir un conjunto de datos  (por ejemplo, una clave) en
(por ejemplo, una clave) en  partes
partes  de manera que:
de manera que:
 (por ejemplo, una clave) en
(por ejemplo, una clave) en  partes
partes  de manera que:
de manera que:- El conocimiento de
 o más
o más  partes hace que
partes hace que  sea fácilmente computable.3
sea fácilmente computable.3 - El conocimiento de
 o menos
o menos  partes hace que
partes hace que  esté indeterminado, en el sentido de que todos sus valores posibles tienen la misma probabilidad de ser verdaderos.
esté indeterminado, en el sentido de que todos sus valores posibles tienen la misma probabilidad de ser verdaderos.
Esta combinación se denomina combinación o esquema de umbral  .2 Si
.2 Si  se requiere la concurrencia de todos los participantes para reconstruir el secreto.
se requiere la concurrencia de todos los participantes para reconstruir el secreto.
 .2 Si
.2 Si  se requiere la concurrencia de todos los participantes para reconstruir el secreto.
se requiere la concurrencia de todos los participantes para reconstruir el secreto.Sistema de compartición de secretos de Shamir
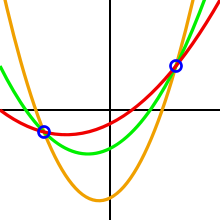
La idea esencial de la combinación de umbral de Shamir es que dos puntos son suficientes para definir una línea recta, tres puntos lo son para definir una parábola, cuatro para definir una curva cúbica y así sucesivamente. Es decir, son necesarios  puntos para definir un polinomio de grado
puntos para definir un polinomio de grado  .
.
 puntos para definir un polinomio de grado
puntos para definir un polinomio de grado  .
.
Supongamos que queremos trabajar con un umbral de  para compartir un secreto
para compartir un secreto  (cualquier número, sin pérdida de generalidad) siendo
(cualquier número, sin pérdida de generalidad) siendo  . La elección de los valores de
. La elección de los valores de  y
y  determina la fortaleza del sistema.
determina la fortaleza del sistema.
 para compartir un secreto
para compartir un secreto  (cualquier número, sin pérdida de generalidad) siendo
(cualquier número, sin pérdida de generalidad) siendo  . La elección de los valores de
. La elección de los valores de  y
y  determina la fortaleza del sistema.
determina la fortaleza del sistema.
Eligiendo al azar 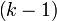 coeficientes
coeficientes 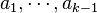 , y siendo
, y siendo 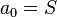 , se construye el polinomio
, se construye el polinomio 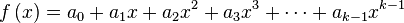 . Calculamos cualesquiera
. Calculamos cualesquiera  puntos a partir del mismo, por ejemplo determinamos que
puntos a partir del mismo, por ejemplo determinamos que  de lo que se deriva
de lo que se deriva 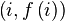 . A todo participante en el secreto se le da un punto (un par de valores, el de entrada y el de salida para el polinomio)
. A todo participante en el secreto se le da un punto (un par de valores, el de entrada y el de salida para el polinomio)
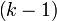 coeficientes
coeficientes 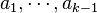 , y siendo
, y siendo 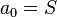 , se construye el polinomio
, se construye el polinomio 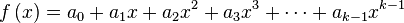 . Calculamos cualesquiera
. Calculamos cualesquiera  puntos a partir del mismo, por ejemplo determinamos que
puntos a partir del mismo, por ejemplo determinamos que  de lo que se deriva
de lo que se deriva 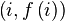 . A todo participante en el secreto se le da un punto (un par de valores, el de entrada y el de salida para el polinomio)
. A todo participante en el secreto se le da un punto (un par de valores, el de entrada y el de salida para el polinomio)
Dado cualquier subconjunto de  entre estos pares, podemos calcular los coeficientes del polinomio mediante interpolación y luego despejar
entre estos pares, podemos calcular los coeficientes del polinomio mediante interpolación y luego despejar  , que es el secreto.
, que es el secreto.
 entre estos pares, podemos calcular los coeficientes del polinomio mediante interpolación y luego despejar
entre estos pares, podemos calcular los coeficientes del polinomio mediante interpolación y luego despejar  , que es el secreto.
, que es el secreto.Ejemplo de uso
Preparación
Supongamos que el secreto es el número de una tarjeta de crédito: 1234 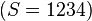 .
.
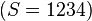 .
.
Queremos dividir el secreto en seis partes 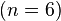 , de forma que cualquier subconjunto
, de forma que cualquier subconjunto  sea suficiente para reconstruir el secreto. Al azar obtenemos
sea suficiente para reconstruir el secreto. Al azar obtenemos  números: por ejemplo, 166 y 94.
números: por ejemplo, 166 y 94.
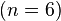 , de forma que cualquier subconjunto
, de forma que cualquier subconjunto  sea suficiente para reconstruir el secreto. Al azar obtenemos
sea suficiente para reconstruir el secreto. Al azar obtenemos  números: por ejemplo, 166 y 94.
números: por ejemplo, 166 y 94.
El polinomio con el que operaremos será por lo tanto:
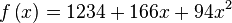
Calculamos seis puntos a partir del polinomio:

Damos a cada partícipe un único punto, que comprende el valor  y
y  ).
).
 y
y  ).
).Reconstrucción
Para reconstruir el secreto bastará con tres puntos.
Considérese
 .
.
Usamos la interpolación polinómica de Lagrange:



Por lo tanto,

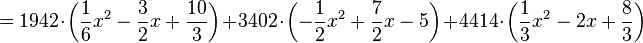

Teniendo en cuenta que el secreto es el coeficiente de
 , el secreto original es
, el secreto original es  .
.
La exponenciación modular es un tipo de exponenciación realizada sobre un módulo. Es particularmente útil en ciencias de la computación, especialmente en el campo de la criptografía.
Una «exponenciación modular» calcula el residuo cuando un número entero positivo b (la base) se eleva a la e-ésima potencia (el exponente), be, y es dividido por el entero positivo m, llamado módulo. En símbolos, esto es, dada la base b, el exponente e, y el módulom, la exponenciación modular c es: 

Por ejemplo, dado b = 5, e = 3, y m = 13, la solución, c = 8, es el resto de dividir  por 13.
por 13.
 por 13.
por 13.
Si b, e, y m no son negativos, y b < m, entonces una única solución c existe con la propiedad 0 ≤ c < m.
La exponenciación modular se puede realizar con exponente negativo e encontrando el inverso multiplicativo modular d de b módulo musando el algoritmo extendido de Euclides. Esto es:
 donde e < 0 y
donde e < 0 y 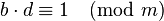
Problemas de exponenciación modular similares al descrito arriba son considerados fáciles de resolver, incluso cuando los números que se manejan son enormes. Por otro lado, el cálculo del logaritmo discreto — es decir, la tarea de encontrar el exponente e si es dado unb, c, y m — se cree que es difícil. Este comportamiento de función unidireccional hace a la exponenciación modular un candidato para su uso en algoritmos criptográficos.
El algoritmo para cálculo de la exponenciación modular
El algoritmo:
| Entrada: números enteros a (base), n (exponente), m (módulo)
Devuelve: un entero exp= an mod m
Restricciones: 0 <= a < m, m >= 2, n >=0 función Exponenciación (entero a, entero n, entero m) : entero |
La idea detrás de la exponenciación modular rápida consiste en obtener la representación del exponente n en dígitos binarios (dt,dt-1,...,d2,d1), con dt =1, y hallar los distintos cuadrados sucesivos (mod m) de la base a: (a1,a2,a4,...,a2t), para después multiplicar módulo m las potencias a2i correspondientes a los dígitos binarios di que sean "1".
Partiendo de esta idea, el algoritmo arriba mostrado se sirve de un bucle en el que en cada iteración se van generando y multiplicando los cuadrados correspondientes, al mismo tiempo que se va dividiendo el exponente n entre 2 (para obtener los dígitos del exponente en binario)
La Firma de Lamport-Diffie es un esquema de firma digital propuesta por L. Lamport y W. Diffie.1 y que está basada en criptografía simétrica . La firma, en principio, se aplica sobre mensajes sin efectuar ninguna modificación previa de los mismos.
Descripción
Para firmar un mensaje M de n bits, el firmante elige aleatoriamente un vector K constituido por n parejas de claves secretas dadas por:
A continuación el firmante calcula dos secuencias de valores R y S dadas por:
donde los valores del conjunto S se escogen de forma aleatoria y los del conjunto R son sus respectivos cifrados dados por:
siendo 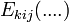 un criptosistema simétrico de clave kij. La estructura del criptosistema E utilizado determina el número de bits n y la longitud de las secuencias R y S utilizadas luego para la validación. Por ejemplo, si E es el DES, entonces n=64. En estas condiciones, los conjuntos R y S se hacen públicos en un registro de sólo lectura, que sólo puede ser modificado por el firmante. La firma
un criptosistema simétrico de clave kij. La estructura del criptosistema E utilizado determina el número de bits n y la longitud de las secuencias R y S utilizadas luego para la validación. Por ejemplo, si E es el DES, entonces n=64. En estas condiciones, los conjuntos R y S se hacen públicos en un registro de sólo lectura, que sólo puede ser modificado por el firmante. La firma  del mensaje
del mensaje 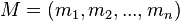 con
con  un bit que puede valer 0 ó 1, será:
un bit que puede valer 0 ó 1, será:
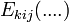 un criptosistema simétrico de clave kij. La estructura del criptosistema E utilizado determina el número de bits n y la longitud de las secuencias R y S utilizadas luego para la validación. Por ejemplo, si E es el DES, entonces n=64. En estas condiciones, los conjuntos R y S se hacen públicos en un registro de sólo lectura, que sólo puede ser modificado por el firmante. La firma
un criptosistema simétrico de clave kij. La estructura del criptosistema E utilizado determina el número de bits n y la longitud de las secuencias R y S utilizadas luego para la validación. Por ejemplo, si E es el DES, entonces n=64. En estas condiciones, los conjuntos R y S se hacen públicos en un registro de sólo lectura, que sólo puede ser modificado por el firmante. La firma  del mensaje
del mensaje 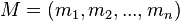 con
con  un bit que puede valer 0 ó 1, será:
un bit que puede valer 0 ó 1, será: .
.
La firma  del mensaje M es obtenida de la siguiente forma: la componente i de
del mensaje M es obtenida de la siguiente forma: la componente i de  será
será 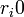 si
si  es 0, en otro caso será
es 0, en otro caso será 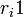 . La autenticidad de la firma
. La autenticidad de la firma  se comprueba verificando las relaciones entre los correspondientes valores de las secuencias de validación R y S en función de las claves conocidas. Sea
se comprueba verificando las relaciones entre los correspondientes valores de las secuencias de validación R y S en función de las claves conocidas. Sea
 del mensaje M es obtenida de la siguiente forma: la componente i de
del mensaje M es obtenida de la siguiente forma: la componente i de  será
será 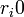 si
si  es 0, en otro caso será
es 0, en otro caso será 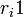 . La autenticidad de la firma
. La autenticidad de la firma  se comprueba verificando las relaciones entre los correspondientes valores de las secuencias de validación R y S en función de las claves conocidas. Sea
se comprueba verificando las relaciones entre los correspondientes valores de las secuencias de validación R y S en función de las claves conocidas. Sea
obtenido de la misma forma que se calculaba  pero ahora en lugar de R, usamos S. Ahora hallamos
pero ahora en lugar de R, usamos S. Ahora hallamos 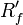
 pero ahora en lugar de R, usamos S. Ahora hallamos
pero ahora en lugar de R, usamos S. Ahora hallamos 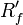
En estas condiciones, el receptor acepta la validez de la firma si dichos valores son respectivamente iguales a los del subconjunto 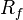 del registro público R (hallado de forma análoga que
del registro público R (hallado de forma análoga que  y
y  , pero esta vez sobre R)
, pero esta vez sobre R)
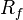 del registro público R (hallado de forma análoga que
del registro público R (hallado de forma análoga que  y
y  , pero esta vez sobre R)
, pero esta vez sobre R)Ejemplo
Sea  un criptosistema simétrico de clave secreta k de n=3 bits. Para computar la firma de M=1011, Primero el firmate elige aleatoriamente el vector binario K de claves secretas, por ejemplo:
un criptosistema simétrico de clave secreta k de n=3 bits. Para computar la firma de M=1011, Primero el firmate elige aleatoriamente el vector binario K de claves secretas, por ejemplo:
 un criptosistema simétrico de clave secreta k de n=3 bits. Para computar la firma de M=1011, Primero el firmate elige aleatoriamente el vector binario K de claves secretas, por ejemplo:
un criptosistema simétrico de clave secreta k de n=3 bits. Para computar la firma de M=1011, Primero el firmate elige aleatoriamente el vector binario K de claves secretas, por ejemplo:
A continuación se elige la secuencia binaria aleatorio S, por ejemplo
y computa el vector R
haciendo públicos los conjuntos R y S. Por tanto la firma  será:
será:
 será:
será:
Para verificarla hallamos  y
y 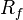 :
:
 y
y 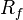 :
:
Para verificar hallamos 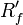 quedando
quedando
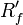 quedando
quedando
que coincide con 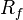 y por tanto el receptor acepta la validez de la firma.
y por tanto el receptor acepta la validez de la firma.
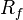 y por tanto el receptor acepta la validez de la firma.
y por tanto el receptor acepta la validez de la firma.Incovenientes
Es conveniente que el firmate cambie el vector de claves secretas K, así como las correspondientes secuencias de validación contenidas en los registro públicos R y S, cada vez que se aplique la firma. En caso contrario, el secreto podría ser revelado, comprometiendo la seguridad.
Otro inconvenientes es el de la excesiva longitud de la firma, de la clave K y de los vectores R y S implicados. Produciendo un gasto de recursos de almacenamiento y de transmisión. Una forma de paliar un poco este inconveniente es firmar el resultado de aplicar una función hash (realmente un código de detección de manipulaciones).
![K=[(k_{10},k_{11}),....,(k_{n0},k_{n1})]](https://upload.wikimedia.org/math/f/4/0/f4033b5b81fd1e754147eb605e5599e0.png)
![S=[(s_{10},s_{11}),...,(s_{n0},s_{n1})]](https://upload.wikimedia.org/math/6/5/e/65e27a311abb1849871047a9ff186924.png)
![R=[(r_{10},r_{11}),...,(r_{n0},r_{n1})]](https://upload.wikimedia.org/math/f/a/c/fac6f1a166e2228dea98b056b8fa8325.png)

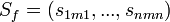
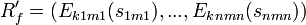
![K=[(000,011),(110,001),(100,111),(010,101)]](https://upload.wikimedia.org/math/9/3/9/939774e4509f2ca7679f67c5b40c158b.png)
![S=[(011,001),(010,111),(100,110),(101,000)]](https://upload.wikimedia.org/math/7/7/d/77d459b01dbd35e415e3bcd399a3dee1.png)
![R=[(011,010),(100,110),(000,001),(111,101)]](https://upload.wikimedia.org/math/2/8/0/2802135bc14bb756ec3fc3a0600ebc9c.png)


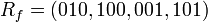
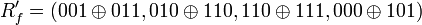
No hay comentarios:
Publicar un comentario