Algoritmos criptográficos
DSA (Digital Signature Algorithm, en español Algoritmo de Firma digital) es un estándar del Gobierno Federal de los Estados Unidos de América o FIPS para firmas digitales. Fue un Algoritmo propuesto por el Instituto Nacional de Normas y Tecnología de los Estados Unidos para su uso en su Estándar de Firma Digital(DSS), especificado en el FIPS 186. DSA se hizo público el 30 de agosto de 1991, este algoritmo como su nombre lo indica, sirve para firmar y no para cifrar información. Una desventaja de este algoritmo es que requiere mucho más tiempo de cómputo que RSA.
Generación de llaves
- Elegir un número primo p de L bits, donde 512 ≤ L ≤ 1024 y L es divisible por 64.
- Elegir un número primo q de 160 bits, tal que p−1 = qz, donde z es algún número natural.
- Elegir h, donde 1 < h < p − 1 tal que g = hz(mod p) > 1.
- Elegir x de forma aleatoria, donde 1 < x < q-1.
- Calcular y = gx(mod p).
Los datos públicos son p, q, g e y. x es la llave privada.
Firma
- Elegir un número aleatorio k, donde 1 < k < q.
- Calcular r = (gk mod p)mod q.
- Calcular s = k-1(H(m)+r*x) mod q, donde H(m) es la función hash SHA-1 aplicada al mensaje m.
- La firma es el par (r, s).
Si r ó s es cero, se vuelve a repetir el procedimiento.
Verificación
- Calcular w = (s)-1(mod q).
- Calcular u1 = H(m)*w(mod q).
- Calcular u2 = r*w(mod q).
- Calcular v = [gu1*yu2mod p] mod q.
- La firma es válida si v = r.
Demostración del algoritmo
El esquema de la firma está correcto en el sentido que el verificador aceptará siempre firmas genuinas. Esto puede ser demostrada como sigue:
El firmante computa
Entonces
Ya que g tiene orden q tenemos que
Finalmente, la correctitud de DSA surge de
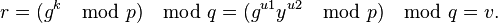
- ECDSA. Elliptic Curve Digital Signature Algorithm es una modificación del algoritmo DSA que emplea operaciones sobre puntos de curvas elípticas en lugar de las exponenciaciones que usa DSA (problema del logaritmo discreto). La principal ventaja de este esquema es que requiere números de tamaños menores para brindar la misma seguridad que DSA o RSA. Existen dos tipos de curvas dependiendo del campo finito en el que se definan que pueden ser GF(P) o GF(2m).
Proceso de firma y verificación
- Generación de llaves
- Seleccione una curva elíptica E.
- Seleccione un punto P (que pertenezca a E) de orden n.
- Seleccione aleatoriamente un número d en el intervalo [1, n - 1].
- Calcule Q = dP.
- d será la llave privada.
- Q será la llave pública.
- Proceso de firma
- Seleccione un número k de forma aleatoria.
- Calcule kP = (x1,y1).
- Calcule r = x1 mod n. Si r = 0 regresa al primer paso. (En este paso x1 es tratado como un entero).
- Calcule (k-1) mod n.
- Calcule s = k-1(H(m) + dr) mod n. Si s = 0 regrese al primer paso. (H(m) es el hash del mensaje a firmar, calculado con el algoritmo SHA-1).
- La firma del mensaje m son los números r y s.
- Proceso de verificación
- Verifique que r y s estén dentro del rango [1,n - 1].
- Calcule w = s-1 mod n.
- Calcule u1 = H(m)w mod n.
- Calcule u2 = r·w mod n.
- Calcule u1P + u2Q = (x0,y0)
- Calcule v = x0 mod n
- La firma verifica si y solo si v = r
- El Esquema de firma ElGamal es un esquema de firma digital basado en la complejidad del cálculo del logaritmo discreto. Fue descrito por Taher ElGamal en 1984. El algoritmo de firma ElGamal descrito en su artículo es raramente utilizado en la práctica. Con más frecuencia se utiliza una de sus variantes llamada Algoritmo de firma digital (DSA). El esquema de firma ElGamal no debe confundirse con el cifrado ElGamal también propuesto por Taher ElGamal.El esquema de firma ElGamal permite que un verificador pueda confirmar la autenticidad de un mensaje m enviado por un emisor sobre un canal de comunicacióninseguro.
Parámetros
Los parámetros utilizados por el esquema ElGamal son:- Una función de hash H resistente a colisiones.
- Un número primo p muy grande tal que el cómputo de logaritmos discretos módulo p sea difícil.
- un generador pseudoaleatorio g para el grupo multiplicativo
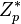 .
.
Los parámetros utilizados pueden ser compartidos entre usuarios.Generación de claves
- Se selecciona un clave secreta x de forma aleatoria tal que
 .
. - Se calcula
 .
. - La clave pública será (p,g,y).
- La clave secreta será x.
Estos pasos son realizados una sola vez por el firmante.Generación de una firma
Para firmar un mensaje m el firmante realiza los pasos siguientes.- Selecciona un número aleatorio k tal que
 y
y 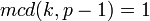 .
. - Calcula
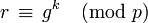 .
. - Calcula
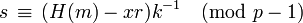 .
. - Si
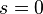 reinicia el proceso.
reinicia el proceso.
El par (r,s) así obtenido es la firma digital de m. El firmante repite estos pasos para cada mensaje m que desea firmar.Verificación
La firma (r,s) de un mensaje m proveniente de un firmante con clave pública (p,g,y) y que utilizó una función de Hash H se verifica de la siguiente forma:- Se verifica que
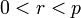 y que
y que 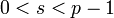 .
. - Se verifica que
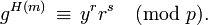 .
.
El verificante acepta el mensaje únicamente si estas tres condiciones se cumplen.Corrección
El algoritmo es correcto en el sentido que una firma generada con este algoritmo de firma siempre será aceptada por un verificador.La generación de firmas incluyeDel pequeño teorema de Fermat se tieneSeguridad
Un tercero puede falsificar firmas si encuentra la clave secreta x del firmante o si encuentra colisiones en la función de Hash . Se considera que ambos problemas son suficientemente difíciles.El firmante debe tener cuidado y escoger una k diferente de forma uniformemente aleatoria para cada firma. Así asegura que k o aún información parcial sobre k no es deducible. Malas selecciones de k pueden representar fugas de información que facilitan el que un atacante deduzca la clave secreta x. En particular, si dos mensajes son enviados con el mismo valor de k entonces es factible deducir el valor de la clave secreta x.
. Se considera que ambos problemas son suficientemente difíciles.El firmante debe tener cuidado y escoger una k diferente de forma uniformemente aleatoria para cada firma. Así asegura que k o aún información parcial sobre k no es deducible. Malas selecciones de k pueden representar fugas de información que facilitan el que un atacante deduzca la clave secreta x. En particular, si dos mensajes son enviados con el mismo valor de k entonces es factible deducir el valor de la clave secreta x.Esquema ElGamal
Recordamos que todo usuario posee una llave pública (pU,xU,yU) y una llave secreta zU, donde p es primo, xU es un elemento primitivo dee
. Se tiene pues:
- Para un entero k aleatorio:
donde
¡Atención! Si se mostrase k entonces podría calcularse la llave secreta zU a partir de la firma:
,
pues en el caso de que (u,e) resultase del proceso de firmar, necesariamente:
yUu ue=xUzU uxUke=xUm
ya que.
Un intruso S que conociese el mensaje m buscaría generar los correspondientes coeficientes (u,e) de la firma. Si conociese u, el exponente e podría conocerse calculando. Si conociese e, el elemento u podría conocerse tratando de reslver la ecuación:
. Algún otro intento consistiría en tratar de calcular simultáneamente u,e. No se conoce de un algoritmo eficiente que lo haga. Tampoco se ha demostrado que no exista tal algoritmo. Sn embargo, de manera aleatoria un intruso podría generar mensajes firmados: Sean
tales que j y p-1 sean primos relativos. Definamos:
Entonces (u,e) es una firma de m con la llave pública (p,x,y). En efecto, módulo p valen las igualadades siguientes:
Un segundo procedimiento para generar firmas legítimas sobre ciertos mensajes es el siguiente: Supongamos conocido unmensaje m con su firma correspondiente (u,e). Seantales quehu-je y p-1 sean primos relativos. Definamos:
Entonces (u',e') es una firma de m' con la llave pública (p,x,y).- Para un entero k aleatorio:
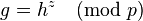 sigue
sigue 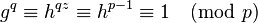 por
por 


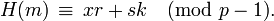

No hay comentarios:
Publicar un comentario