Algoritmos criptográficos
En criptografía, el cifrado XOR es, como su nombre indica, un algoritmo de cifrado basado en el operador binario XOR:
- A
 0 = A,
0 = A,
- A
 A = 0,
A = 0,
- (B
 A)
A)  A = B
A = B  0 = B,
0 = B,
Donde  es una operación OR exclusiva (XOR). Una cadena de texto puede ser cifrada aplicando el operador de bit XOR sobre cada uno de los caracteres utilizando una clave. Para descifrar la salida, solo hay que volver a aplicar el operador XOR con la misma clave.
es una operación OR exclusiva (XOR). Una cadena de texto puede ser cifrada aplicando el operador de bit XOR sobre cada uno de los caracteres utilizando una clave. Para descifrar la salida, solo hay que volver a aplicar el operador XOR con la misma clave.
 es una operación OR exclusiva (XOR). Una cadena de texto puede ser cifrada aplicando el operador de bit XOR sobre cada uno de los caracteres utilizando una clave. Para descifrar la salida, solo hay que volver a aplicar el operador XOR con la misma clave.
es una operación OR exclusiva (XOR). Una cadena de texto puede ser cifrada aplicando el operador de bit XOR sobre cada uno de los caracteres utilizando una clave. Para descifrar la salida, solo hay que volver a aplicar el operador XOR con la misma clave.
Por ejemplo, la cadena "Wiki" (01010111 01101001 01101011 01101001 en 8-bit ASCII) puede ser cifrada con la clave 11110011 de la siguiente manera:
01010111 01101001 01101011 01101001 
11110011 11110011 11110011 11110011 = 10100100 10011010 10011000 10011010
Y viceversa para descifrarlo:
10100100 10011010 10011000 10011010 
11110011 11110011 11110011 11110011 = 01010111 01101001 01101011 01101001
El operador XOR es muy común como parte de cifrados más complejos. Sin embargo, por sí solo el cifrado XOR es muy vulnerable y es muy fácil obtener la clave a través del análisis de varios mensajes cifrados con la misma clave.
Explicando el metodo del XOR
El metodo se realiza de la siguiente forma:
Como se hace a nivel de bits se cuenta con la siguiente tabla
Como se hace a nivel de bits se cuenta con la siguiente tabla
| Entrada A | Entrada B | Salida A  B B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Tabla extraida de la wikipedia
Tenemos una palabra que queremos cifrar :
BACK
Tenemos una clave alfanumerica:
DOOR
Para poder comparar estas dos palabras se tienen que convertir a su equivalente en Ascii binario para realizar las operaciones:
Para poder comparar estas dos palabras se tienen que convertir a su equivalente en Ascii binario para realizar las operaciones:
B=0100001
A=1000001
C=1100001
K=1101001
A=1000001
C=1100001
K=1101001
D=0010001
O=1111001
O=1111001
R=0100101
O=1111001
O=1111001
R=0100101
Una vez que se realiza el cambio se efectua la operacion XOR:
0100001 1000001 1100001 1101001
0010001 1111001 1111001 0100101
————– ————– ————– —————
0110000 0111000 0011000 1001100
————– ————– ————– ————–
45 56 24 76
0010001 1111001 1111001 0100101
————– ————– ————– —————
0110000 0111000 0011000 1001100
————– ————– ————– ————–
45 56 24 76
Se hace el primer caracter del texto plano con el primer caracter de la clave , el segundo del texto plano con el segundo caracter de la clave y asi sucesivamente si se acaba los caracteres de la clave se empieza de nuevo con el primero.
Lo que hice en el ejemplo de arriba fue hacer la operacion XOR en binario y el resultado volverlo nuevamente a decimal.
El resultado de nuestro texto cifrado seria:
El resultado de nuestro texto cifrado seria:
– 8 (CAN) L
La palabra CAN es el simbolo de cancel entonces lo mas seguro les saldra (si lo implementan en una computadora) un cuadrado pequenio.


Common Scrambling Algorithm (CSA) és un algoritmo de cifrado utilizado para proteger streams de vídeo en redes de difusión DVB (Digital Video Broadcasting). La televisión digital por pago en Europa y algunos proveedores de televisión por satélite usan este algoritmo para proteger sus emisiones de la decodificación ilegal.
Historia
El CSA se utiliza para proteger transport streams de estandard MPEG-2. Fue especificado por ETSI y adoptado por el consorcio DVB en mayo de 1994, aunque realmente no se empezó a conocer hasta primavera de 2002 (mantenido prácticamente en secreto durante un largo período). Sin embargo, la fecha en la que se empezó a diseñar no ha quedado del todo clara.
Antes de 2002 poco se conocía sobre este algoritmo de seguridad, solo pequeña información como un reportaje técnico de ETSI 'Eur96' y usos evidentes 'Bew98','WAJ98' lo dieron a conocer, aunque nunca detalladamente, de forma publica. En otoño del 2002 apareció un programa para Windows conocido como FreeDecque implementaba el CSA en software. Esto permitió que se corrigieran pequeños errores y por lo tanto la reimplementación del algoritmo en lenguajes de programación de más alto nivel. Las especificaciones se pueden obtener a través de ETSI: debido a que los detalles del CSA están ligados a la seguridad de la difusión de las señales, las especificaciones no han sido publicadas aunque las compañías que desen disponer del servicio pueden conseguirlas siempre y cuando se firme un contrato de confidencialidad.
Características
CSA es una combinación de dos algoritmos: un cifrado block y un cifrado stream. Ambos tiene la misma llave, lo que quiere decir que con atacar a uno de los 2 se podría romper el algoritmo.
CSA se basa en el principio de cifrado simétrico. Esto significa que el transmisor y el receptor utilizan la misma llave. La llave del algoritmo usa 64 bits lo que da muchas posibilidades (1019 combinaciones). Este gran número de combinaciones da una idea de lo complicado de resolverlo ya que si tardáramos 1 μs por cada intento nos supondría aproximadamente más de 100.000 años de media. De los 64 bits en realidad solo desconocemos 48 bits, desde el byte 3 al 7 son usados como bytes de control y pueden ser fácilmente recalculados. Esto permite ahorrar tiempo de ataque donde 32 bits reciben un ataque de fuerza bruta, 16 bits son calculados con tablas de memoria construidas desde un texto cifrado y 16 bits calculados como suma de verificación con un tiempo de arranque de O(216)+O(232), lo que nos llevaría menos de 1 segundo si lo implementamos en una arquitectura hardware FPGA.
La llave para descodificar flujos de datos de vídeo actualmente cambia cada aproximadamente 10 segundos, lo que en un principio asegura que no se pueda romper la protección de cualquier forma y salvaguardar así los derechos de la televisión por pago.
En el caso de romper el algoritmo, las transmisiones codificadas DVB serían descifrables, independientemente del sistema de acceso usado. Esto podría comprometer seriamente la televisión digital por pago en Europa y en otros lugares ya que muchos proveedores de televisión por satélite usan CSA. La no publicación en detalle del algoritmo hace que CSA sea una fuerte medida de seguridad ahora y durante un largo período.
Merkle-Hellman (MH) fue uno de los primeros criptosistemas de llave pública y fue inventado por Ralph Merkle y Martin Hellman en 1978.1 Aunque sus ideas eran elegantes, y mucho más simples que RSA, no tuvo el mismo éxito que éste último, debido a que MH ya fue roto,2 y además no ofrece funcionalidades para firmar.
Descripción
Merkle-Hellman es un criptosistema asimétrico, esto significa que para la comunicación, se necesitan dos llaves: una llave pública y una privada. Otra diferencia con RSA, es que sirve sólo para cifrado, es decir, la llave pública es usada sólo para cifrar (no para verificar firma) y la llave privada es usada sólo para descifrar (no para firmar). De este modo, no se puede usar para tareas de autentificación por firma electrónica.
El algoritmo de Merkle-Hellman está basado en el problema de la mochila de decisión (un caso especial del problema de la mochila de optimización): dados una secuencia de números y un número, determinar si existe un subconjunto de la secuencia cuya suma dé dicho número. En general, es sabido que este problema es de clase NP-completo. Sin embargo, si la secuencia de números es supercreciente -- esto es, si cada elemento de la secuencia es mayor que la suma de todos los anteriores -- el problema es "fácil", y es posible resolverlo en tiempo polinómico con un simple algoritmo voraz.
Generación de las claves
En Merkle-Hellman, las claves están compuestas por secuencias. La clave pública es una secuencia "difícil", y la clave privada es una "fácil", o secuencia de valores supercrecientes, junto con dos números adicionales, un multiplicador y un módulo, los cuales son usados para convertir la secuencia supercreciente en una secuencia difícil. Estos mismos números son usados para transformar la suma de la subsecuencia de la secuencia "difícil" en la suma de la subsecuencia de la secuencia "fácil", la cual se puede solucionar en tiempo polinómico.
Cifrado
Para cifrar un mensaje, el cual debe ser una secuencia de bits de la misma longitud de la secuencia difícil, se eligen los elementos de la secuencia difícil que correspondan a bits en 1 del mensaje (mientras que los elementos correspondientes a bits en 0 son descartados). Luego se suman los elementos así elegidos, y el resultado de esto es el texto cifrado.
En caso que el mensaje no sea de la misma longitud de la llave, se subdivide en secuencias que tengan esta longitud y se aplica el mismo procedimiento.
Descifrado
El descifrado es posible, porque el multiplicador y el módulo usados para transformar la secuencia supercreciente (la llave privada) y por tanto "fácil" en la secuencia general (la llave pública) y por tanto difícil, también pueden ser usados para transformar el texto cifrado (representado por un número) en la suma de los elementos que conforman la subsecuencia supercreciente (una subsecuencia de una secuencia supercreciente, también es supercreciente). Luego, usando un algoritmo voraz, el problema "fácil" de la mochila puede ser resuelto usando O(n) operaciones, con lo cual se logra descifrar el mensaje.
Método Matemático
Generación de las claves
Para cifrar un mensaje de n-bits, elegir una secuencia supercreciente :
de n números naturales (distintos de cero). Elegir un número q (preferiblemente al azar), tal que
y otro número entero, r tal que mcd(r,q) = 1.
q es escogido de esta forma para asegurar la unicidad del texto cifrado. Si fuera menor, podría haber varios textos claros que resultarían en el mismo texto cifrado. rdebe ser coprimo con q puesto que de otra forma podría no tener inverso en 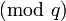 . La existencia del inverso de r es necesaria para que se pueda realizar el descifrado.
. La existencia del inverso de r es necesaria para que se pueda realizar el descifrado.
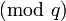 . La existencia del inverso de r es necesaria para que se pueda realizar el descifrado.
. La existencia del inverso de r es necesaria para que se pueda realizar el descifrado.
A continuación, se calcula la secuencia:
La clave pública es  , mientras que la llave privada es
, mientras que la llave privada es  .
.
 , mientras que la llave privada es
, mientras que la llave privada es  .
.Cifrado
Para cifrar un mensaje de n-bits
donde  es el i-ésimo bit del mensaje y
es el i-ésimo bit del mensaje y 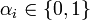 , calcular
, calcular
 es el i-ésimo bit del mensaje y
es el i-ésimo bit del mensaje y 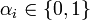 , calcular
, calcular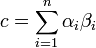 .
.
El criptograma o texto cifrado es c.
Descifrado
Para descifrar el criptograma c, el receptor tiene que encontrar los bits del mensaje 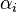 tales que satisfacen
tales que satisfacen
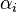 tales que satisfacen
tales que satisfacen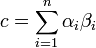 .
.
Este problema sería difícil de resolver si los  fueran valores aleatorios, debido a que el receptor tendría que resolver una instancia del problema de la mochila, el cual se sabe que es NP-hard. Sin embargo, los valores
fueran valores aleatorios, debido a que el receptor tendría que resolver una instancia del problema de la mochila, el cual se sabe que es NP-hard. Sin embargo, los valores  fueron elegidos de forma que el descifrado sea fácil si la clave privada
fueron elegidos de forma que el descifrado sea fácil si la clave privada  es conocida.
es conocida.
 fueran valores aleatorios, debido a que el receptor tendría que resolver una instancia del problema de la mochila, el cual se sabe que es NP-hard. Sin embargo, los valores
fueran valores aleatorios, debido a que el receptor tendría que resolver una instancia del problema de la mochila, el cual se sabe que es NP-hard. Sin embargo, los valores  fueron elegidos de forma que el descifrado sea fácil si la clave privada
fueron elegidos de forma que el descifrado sea fácil si la clave privada  es conocida.
es conocida.
Para el descifrado se debe encontrar un entero s tal que es el inverso de r módulo q. Esto es, s satisface la ecuación :
o equivalentemente, existe un entero k tal que sr = kq + 1. Dado que r fue escogido como un coprimo de q es posible encontrar s y k usando el Algoritmo de Euclides extendido. Luego el receptor del criptograma c calcula:
Por tanto
Ya que  y
y  entonces
entonces
 y
y  entonces
entonces
Con esto
La suma de todos los valores  es menor que q y por ende
es menor que q y por ende  también está en el intervalo
también está en el intervalo ![\mathbf [0,q-1]](https://upload.wikimedia.org/math/2/f/7/2f7a2f4118033f1ab073690fa4b59819.png) .
.
 es menor que q y por ende
es menor que q y por ende  también está en el intervalo
también está en el intervalo ![\mathbf [0,q-1]](https://upload.wikimedia.org/math/2/f/7/2f7a2f4118033f1ab073690fa4b59819.png) .
.
De este modo el receptor tiene que resolver el siguiente problema de la mochila.
Este problema es fácil debido a que la secuencia w es supercreciente.
El algoritmo avaro para resolver esto consiste en lo siguiente:
Tomar el elemento más grande en, digamos
. Si
, luego
, Sino
Disminuímos c' en
y repetimos estos pasos hasta que se haya alcanzado c'.
El pseudo código para este algoritmo sería:
While{
If
then
, Else

}
Este algoritmo no se puede usar para firmar puesto que el criptograma es un número (c) y no un texto, de este modo no se puede descifrar un mensaje claro y por ende no se puede firmar.
El primero cryptosyst a clave pública, que fue propuesto por Rafael Merkle (fotografía de izquierda) y Martin Hellman en 1978, se basa en el problema de la mochila (Knapsack problem en inglés). No se utiliza actualmente ya puesto que esta cifra, así como de numerosas alternativas, se rompió a principios de los años 80 por Adi Shamir.
El problema de la mochila consiste en amontonar objetos en un bolso, para alcanzar (si es posible) un peso total fijado. Más formalmente, 'danse de los pesos enteros P1..., Pn y y un objetivo T, se trata de encontrar b1..., bn, valiendo 0 o 1, como
Si la consecuencia de los pesos Pk es supercroiss (cada peso es estrictamente superior a la suma de todos los precedentes), entonces existe un método de Resolución simple (algoritmo glouton):
| Algoritmo gloutonPara I = n a 1 hacer Si T = T - Pi bi = 1 si no bi = 0 Si T = 0 entonces {b1..., bn} es solución si no no hay solución. |
Al contrario, si la consecuencia de los pesos no es supercroiss, el único algoritmo conocido consiste en intentar sucesivamente todas las soluciones (b1, b2..., bn) posibles. Si la consecuencia es suficientemente larga, es un algoritmo impracticable.
La cifra de Merkle-Hellman
Es una cifra a clave pública, basada en la dificultad solucionar el problema de la mochila con una consecuencia de peso no supercroiss. Se va de la siguiente observación:
| El problema de la mochila es homogéneo : no cambia las soluciones multiplicando (o dividiendo) todos los pesos Pi y el objetivo T por una misma totalidad p. |
Las multiplicaciones pueden efectuarse módulo una totalidad el Sr. Entonces, aunque la consecuencia de peso inicial es supercroiss, la nueva consecuencia así obtenida no lo será en general. En la práctica, se elige m superior a la suma de los pesos iniciales.
Ejemplo. Va de la consecuencia supercroiss 1,.3,.6. Se hacen todos los cálculos módulo 12. Al multiplicar todos los pesos por 7 se obtiene la consecuencia no supercroiss 7,.9,.6. Gracias a la propiedad de homogeneidad, se ven que la misma solución (b1, b2, b3) permite realizar el objetivo T con los pesos 1,.3,.6 y el objetivo Tx7 con los pesos 7,.9, 6. El cuadro siguiente da la correspondencia entre los objetivos y las soluciones:
| T | Tx7 | b1, b2, b3 |
| 0 | 0 | 0, 0,.0 |
| 1 | 7 | 1, 0,.0 |
| 3 | 9 | 0, 1,.0 |
| 4 | 4 | 1, 1,.0 |
| 6 | 6 | 0, 0,.1 |
| 7 | 1 | 1, 0,.1 |
| 9 | 3 | 0, 1,.1 |
| 10 | 10 | 1, 1,.1 |
Para calcular un bloque de k bites, se calcula simplemente el peso T resultando del bolso. Para garantizar que el descifrado con la misma clave es imposible, se calcula con la consecuencia no supercroiss.
Para descifrar, se deben determinar los pesos cuya suma realiza el objetivo T. la idea consiste en corresponder a la consecuencia supercroiss inicial, sin cambiar la solución. Basta para eso con dividir todos los pesos y el objetivo T por p.
La consecuencia no supercroiss constituye la clave pública. La consecuencia supercroiss inicial, con p y m, forman la clave privada.
Para descifrar, se deben determinar los pesos cuya suma realiza el objetivo T. la idea consiste en corresponder a la consecuencia supercroiss inicial, sin cambiar la solución. Basta para eso con dividir todos los pesos y el objetivo T por p.
La consecuencia no supercroiss constituye la clave pública. La consecuencia supercroiss inicial, con p y m, forman la clave privada.
Primer ejemplo de codificación/descifrado
La clave privada de Bob es [1, 3, 6], con p = 7 y m = 12.
Con la clave pública [7,.9,.6] proporcionada por Bob, Alice calcula así la cadena 101: T = 7x1 + 9x0 + 6x1 = 13 envía pues el mensaje "13" a Bob.
Para descifrar el mensaje, Bob utiliza su clave privada (tienen en cuenta que 7 son su propio opuesto módulo 12), y aplica el algoritmo glouton. Obtiene:
Más generalmente, para que p sea inversible módulo m, basta con elegirlo primero con m.
Es importante tener en cuenta que un texto calculado con la clave privada no podrá descifrarse con la clave pública, puesto que no es supercroiss: las dos claves de la cifra de Merkle-Hellman no pueden permutarse.
Segundo ejemplo de codificación/déchifrement
Al utilizar 5 bites, se pueden cifrar 25 = 32 caracteres. Supongamos que se utiliza la tabla de los 30 caracteres siguientes (este cuadro les recuerda quizá el alfabeto bilit de Bacon):
| a | 00000 | g | 00110 | m | 01100 | s | 10010 | allí | 11000 | ||||
| b | 00001 | h | 00111 | n | 01101 | t | 10011 | z | 11001 | ||||
| c | 00010 | I | 01000 | o | 01110 | u | 10100 | , | 11010 | ||||
| d | 00011 | j | 01001 | p | 01111 | v | 10101 | . | 11011 | ||||
| e | 00100 | k | 01010 | q | 10000 | w | 10110 | ¿? | 11100 | ||||
| f | 00101 | l | 01011 | r | 10001 | x | 10111 | 11101 |
La clave privada de Bob es [3, 4, 9, 19, 38, 77], con p = 27 y m = 155. Puede ahora calcular la clave pública con la cual Alice calculará su mensaje: [ 3x27 (mod 155), 4x27 (mod 155), 9x27 (mod 155), 19x27 (mod 155), 38x27 (mod 155), 77x27 (mod 155) ], lo que da [81, 108, 88, 48, 96, 64].
Alice quiere transmitir la palabra "niño" a Bob. Deberá pues, refiriéndose a la tabla aquí arriba, calcular la cadena 00001.00000.00001 11000. como la clave pública de Bob implica 6 números, ella deberá a continuación agrupar estos bites por paquetes de 6, y si es preciso añadir bites aleatorios para obtener un número de bites múltiple el 6: 000010.000000.001110.001101
El primer bloque de 6 bites se calculará: 81x0 + 108x0 + 88x0 + 48x0 + 96x1 + 64x0 = 96.
El segundo bloque de 6 bites se calculará: 81x0 + 108x0 + 88x0 + 48x0 + 96x0 + 64x0 = 0.
El tercer bloque de 6 bites se calculará: 81x0 + 108x0 + 88x1 + 48x1 + 96x1 + 64x0 = 232.
El cuarto bloque de 6 bites se calculará: 81x0 + 108x0 + 88x1 + 48x1 + 96x0 + 64x1 = 200.
El segundo bloque de 6 bites se calculará: 81x0 + 108x0 + 88x0 + 48x0 + 96x0 + 64x0 = 0.
El tercer bloque de 6 bites se calculará: 81x0 + 108x0 + 88x1 + 48x1 + 96x1 + 64x0 = 232.
El cuarto bloque de 6 bites se calculará: 81x0 + 108x0 + 88x1 + 48x1 + 96x0 + 64x1 = 200.
El mensaje codificado es pues: [ 96,.0,.232,.200 ]
Para descifrar, Bob calcula en primer lugarel revés módulo 155 27, que vale 23. Utiliza a continuación su clave privada y aplica el algoritmo glouton. Obtiene entonces:
El mensaje descifrado es pues [ 000010,.000000,.001110,.001101 ], lo que es el mensaje bien que había enviado Alice.
Para encontrar la palabra, Bob no tiene ya que a agrupar los bites por paquetes de 5 y consultar el cuadro de conversión.
Para encontrar la palabra, Bob no tiene ya que a agrupar los bites por paquetes de 5 y consultar el cuadro de conversión.
Es importante que el número de bites por paquete sea diferente de la longitud de la clave. En efecto, si no era el caso, se podría impugnar el texto calculado por un análisis de las frecuencias, ya que cada carta sería calculada por el mismo número.
Queda claro que más la clave es larga más, el mensaje será difícil de descifrar. En la práctica, se utilizan al menos 250 números en la clave y se elige el módulo m para para tener una longitud incluida entre 100 y 200 bites.








No hay comentarios:
Publicar un comentario