AMIGOS PARA SIEMPRE: Criptografía

Algoritmos criptográficos

Los Códigos de detección de manipulaciones son también llamados Códigos de detección de modificaciones, MDC (siglas del los dos términos ingleses válidos:Modification Detection Codes y Manipulation Detection Codes), Código de integridad de mensajes y MIC (siglas del inglés Message Integrity Codes). Un código de detección de modificaciones es una función hash criptográfica sin clave secreta que puede ser usada para detectar cualquier modificación de la cadena a la cual se aplique, ya sea esta modificación accidental o malintencionada. Por tanto las MDC permiten proteger la integridad de la información.

El modo de funcionamiento consiste en calcular el valor hash de la cadena y que este sirva como evidencia para la verificación de si la cadena ha sido modificada o no.

Para cumplir su objetivo la función hash tiene que cumplir propiedades que la hagan resistente frente ataques de adversarios maliciosos cuyo objetivo es que la función no cumpla con su cometido. Según las propiedades que se exijan podemos distinguir dos tipos de códigos de detección de modificaciones:

Las que requieren que la función hash sea OWHF. Por tanto es difícil encontrar un mensaje que tenga un valor hash pre-especificado.
Las que requieren que la función hash sea CRHF. Por tanto es difícil encontrar dos mensajes con el mismo valor hash.

Métodos de construcción¹ ²

Atendiendo a en que basan su algoritmo podemos clasificar los códigos de detección de modificaciones en:

Basadas en aritmética modular

Estos códigos de detección de modificaciones basan su construcción y por tanto su seguridad en la dificultad de problemas de la aritmética modular. Al poder cambiar fácilmente el valor de referencia con el que se calcula el módulo, es fácil variar la longitud de las cadenas de salida. Estas funciones aprovechan la facilidad de implementación de la función módulo. Suelen ser muy lentos comparados con otro tipo de construcciones.Ejemplo de este tipo de algoritmos es MASH-1 (Modular Arithmetic Secure Hash Algorithm-1).

Basadas en cifradores de bloque

Este tipo de códigos de detección de modificaciones basan su construcción en la reutilización de cifradores de bloque. De esta forma se minimiza el esfuerzo de diseño e implementación y además aprovechan la fiabilidad en la seguridad de esos cifradores para transformar en seguridad en la función hash. En general suelen ser lentos comparados con las llamadas funciones hash dedicadas.

Los siguientes esquemas son los más habituales:

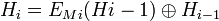
Davies-Meyer(DM): $H_i=E_{Mi} (Hi-1) \oplus H_{i-1}$
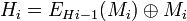
Matyas-Meyer-Oseas (MMO): $H_i= E_{Hi-1}(M_i) \oplus M_i$
Miyaguchi-Preenel: $H_i= E_{Hi-1} (M_i) \oplus M_i \oplus H_{i-1}$

Donde:

$\oplus$ representa al xor
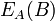$E_{A}(B)$ representa a aplicar el cifrador de bloque E con la clave A sobre el dato B.
$M_i$ es el bloque i del mensaje al que se le aplica la función hash en cada paso.
$H_{i-1}$ es el valor hash obtenido en el paso previo al paso i.

Funciones hash dedicadas

Son códigos de detección de modificaciones especialmente diseñadas desde el principio para este propósito teniendo en cuenta que tengan un rendimiento optimizado y sin tener que reutilizar componentes previamente construidos. Estas funciones no están basadas en problemas difíciles como factorización o logaritmos discretos. Suelen ser construidas usando la construcción de Merkle-Damgård.

Ejemplos: MD2, MD4, MD5, SHA-1, SHA-2, TIGER, HAVAL, RIPEMD, RIPEMD-160, HAIFA, FORK256 y WHIRLPOOL

Ataques

Los código de detección de manipulaciones son sometidos a distintos tipos de ataques. Cada tipo tiene como objetivo debilitar la seguridad desde un punto de vista distintos. Los principales son los siguiente:

Ataque de colisiones.- Se llama ataque de colisiones al proceso de encontrar dos valores arbitrarios cuyos hashes colisionan. Por tanto se ataca la resistencia a colisiones de la función hash.
Ataque preimagen.- Se llama ataque preimagen al proceso de encontrar un valor arbitrario cuyo hash colisione con otro hash dado. Por tanto se ataca laresistencia a preimagen de la función hash. Ejemplos exitosos de este tipo de ataques se han hecho utilizando o apoyándose en estrategias meet in the middle.

Un ataque preimagen exitoso es mucho más serio que un ataque de colisiones exitoso ya que la seguridad de muchas de las aplicaciones que emplean este tipo de funciones están basada en la resistencia a preimagen. Además romper la resistencia a preimagen implica muchas veces romper la resistencia a colisiones.

En el estudio de las colisiones son importantes:

Principio de Dirichlet también llamado Principio del palomar.
Paradoja del cumpleaños.

Diffie-Hellman,¹ debido a Whitfield Diffie y Martin Hellman (autores también del problema de Diffie-Hellman o DHP), es un protocolo de establecimiento de claves entre partes que no han tenido contacto previo, utilizando un canal inseguro, y de manera anónima (no autentificada).

Se emplea generalmente como medio para acordar claves simétricas que serán empleadas para el cifrado de una sesión (establecer clave de sesión). Siendo no autenticado, sin embargo, provee las bases para varios protocolos autenticados.

Su seguridad radica en la extrema dificultad (conjeturada, no demostrada) de calcular logaritmos discretos en un cuerpo finito.

Versión básica

El sistema se basa en la idea de que dos interlocutores pueden generar conjuntamente una clave compartida sin que un intruso que esté escuchando las comunicaciones pueda llegar a obtenerla.

Para ello cada interlocutor elige un número público y un número secreto. Usando una fórmula matemática, que incluye la exponenciación, cada interlocutor hace una serie de operaciones con los dos números públicos y el secreto. A continuación los interlocutores se intercambian los resultados de forma pública. En teoría revertir esta función es tan difícil como calcular un logaritmo discreto (Un millón de millones de cuadrillones más costosa que la exponenciación usada para transformar los números). Por eso se dice que este número es el resultado de aplicar una función unidireccional al número secreto.

A continuación ambos interlocutores utilizan por separado una fórmula matemática que combina los dos números transformados con su número secreto y al final los dos llegan al mismo número resultado que será la clave compartida.

Descripción detallada

Diffie-Hellman.

Para dos partes Alice y Bob que intentan establecer una clave secreta y un adversario Mallory, la versión básica es como sigue:

Se establecen un primo $p$ y un generador $g \in \mathbf{Z}_{p}^{*}$ (² ). Estos son públicos, conocidos no solo por las partes Alice y Bob sino también por el adversario Mallory .
Alice escoge $a \in \mathbf{Z}_{p-1}$ al azar, calcula $A = g^{a} \;\bmod\; p$ , y envía $A$ a Bob
Bob escoge 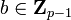$b \in \mathbf{Z}_{p-1}$ al azar, calcula $B = g^{b} \;\bmod\; p$ , y envía $B$ a Alice

Nótese que tanto A como B pueden calcular el valor

K=g^{a \cdot b} \;\bmod\; p

. En efecto, lo podemos demostrar usando las propiedades del grupo

\mathbf{Z}_{p}^{*}

Para Alice:

B^{a} \;\;\bmod\;\; p = (g^b \;\bmod\; p )^a \;\bmod\; p = ( \overbrace{(g^b \;\bmod\; p ) (g^b \;\bmod\; p ) \cdots (g^b \;\bmod\; p ) }^a ) \;\bmod\; p = g^{b \cdot a} \;\bmod\; p= g^{a \cdot b} \;\bmod\; p = K

Para Bob:

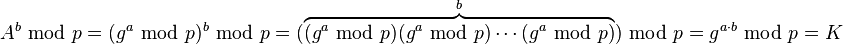
A^{b} \;\bmod\; p = (g^a \;\bmod\; p )^b \;\bmod\; p = ( \overbrace{(g^a \;\bmod\; p ) (g^a \;\bmod\; p ) \cdots (g^a \;\bmod\; p ) }^b ) \;\bmod\; p = g^{a \cdot b} \;\bmod\; p = K

Como ambas partes pueden calcular

K

entonces la podemos usar como clave compartida.

Ataques

Ataques pasivos

Un adversario Mallory que poseyera p, g, A y B, podría calcular el secreto compartido si tuviera también uno de los valores privados (a o b). Obtener a o b a partir de Ao B invirtiendo la función (

a=\operatorname{log\;disc}_p(A)

b=\operatorname{log\;disc}_p(B)

) es el problema del logaritmo discreto en

\mathbf{Z}_{p}^{*}

, un problema que se cree intratable computacionalmente siempre que p sea un número primo grande de 200 o más dígitos y que no cumplan ciertas características debilitantes.³

Ataques activos

El protocolo es sensible a ataques activos del tipo Man-in-the-middle. Si la comunicación es interceptada por un tercero, éste se puede hacer pasar por el emisor cara al destinatario y viceversa, ya que no se dispone de ningún mecanismo para validar la identidad de los participantes en la comunicación. Así, el "hombre en el medio" podría acordar una clave con cada participante y retransmitir los datos entre ellos, escuchando la conversación en ambos sentidos. Una vez establecida la comunicación simétrica el atacante tiene que seguir en medio interceptando y modificando el tráfico para que no se den cuenta. Observar que para que el ataque sea operativo el atacante tiene que conocer el método de cifrado simétrico que será utilizado. Basarse en la ocultación de algoritmo simétrico de cifrado no cumple con los principios de Kerckhoffs (la efectividad del sistema no debe depender de que su diseño permanezca en secreto).

Ataque man-in-the-middle en Diffie-Hellman.

Para evitar este tipo de ataque se suele usar una o más de las siguientes técnicas:

Control de tiempos
Autenticación previa de las partes. Por ejemplo usar en protocolo de capa subyacente autenticación. Podríamos primero establecer una conexión TLS y sobre esa capa aplicar el algoritmo de Diffie-Hellman
Autenticación del contenido. Por ejemplo podríamos usar MAC sobre el contenido de los mensajes
Cifrando las claves públicas con un algoritmo de clave pública (asimétrico), evitando el problema de Man-in-the-middle, y a su vez comprobando que la clave pública sea distinta de 0 y 1.

Ejemplo

Alice
Sec		Calc
	p, g
a
		g^a mod p
	…
	(g^b mod p)^a mod p

$\rightarrow$

$\leftarrow$

Bob
Calc		Sec
	p, g
		b
	…
g^b mod p
	(g^a mod p)^b mod p

Alice y Bob acuerdan usar el número primo p=23 y la base g=5.
Alice elige un número secreto a=6, luego envía a Bob (g^a mod p)
- 5⁶ mod 23 = 8.
Bob elige un número secreto b=15, luego envía a Alice (g^b mod p)
- 5¹⁵ mod 23 = 19.
Alice calcula (g^b mod p)^a mod p
- 19⁶ mod 23 = 2.
Bob calcula (g^a mod p)^b mod p
- 8¹⁵ mod 23 = 2.

Ejemplo con implementación de cifrado

La necesidad para este ejemplo es: Bob necesita enviarle un texto cifrado a Alice pero sin compartir la clave de cifrado. ¿Como lo hace?

Alice elige un número secreto a=6, el número primo p=23 y la base g=5. Luego envía a Bob la llave pública de Alice (g^a mod p), p y g:
- 5⁶ mod 23 = 8.
- 23
- 5
Bob elige un número secreto b=15, luego Bob calcula la llave de cifrado común (g^a mod p)^b mod p
- 8¹⁵ mod 23 = 2.
Bob cifra, con un cifrador simétrico como AES, el texto claro usando la llave de cifrado generada.
TextoCifrado = CifradorSimetrico ( TextoClaro, 2 )
Bob envía a Alice el texto cifrado y la llave pública de Bob (g^b mod p)
- 5¹⁵ mod 23 = 19.
- TextoCifrado
Alice calcula (g^b mod p)^a mod p
- 19⁶ mod 23 = 2.
Alice usa esa clave de cifrado generada para descifrar los datos enviados por Bob
TextoClaro = DescifradorSimetrico ( TextoCifrado, 2 )

Valores mucho más grandes de a,b y p se necesitarían para hacer este ejemplo seguro. Dado que es muy sencillo probar todos los valores posibles de g^ab mod 23 (habrá, como máximo, 22 valores, inclusive si a y b son números grandes).

Obviamente la necesidad de Alice enviarle a Bob la información cifrada también la cubre la implementación.

Generalizaciones

Aumentando el número de partes

La idea del algoritmo podemos generalizarla a la negociación de claves entre más de dos entidades. Veamos un ejemplo para tres entidades y a partir de ahí podemos aumentar el número de partes de forma fácil:

Las partes (Alice, Bob y Carol) se ponen de acuerdo en los parámetros del algoritmo $p$ and $g$ .
Las partes generan sus propias claves privadas llamadas $a$ , $b$ , y $c$ respectivamente.
Alice calcula 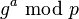$g^a \;\bmod\; p$ y lo envía a Bob.
Bob calcula 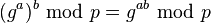$(g^a)^b \;\bmod\; p= g^{ab} \;\bmod\; p$ y lo envía a Carol.
Carol calcula 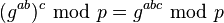$(g^{ab})^c \;\bmod\; p = g^{abc} \;\bmod\; p$ y la usa como su clave secreta.
Bob calcula $g^b \;\bmod\; p$ y lo envía a Carol.
Carol calcula 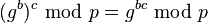$(g^b)^c \;\bmod\; p= g^{bc} \;\bmod\; p$ y lo envía a Alice.
Alice calcula $(g^{bc})^a \;\bmod\; p= g^{bca} \;\bmod\; p= g^{abc} \;\bmod\; p$ y lo usa como su clave secreta.
Carol calcula 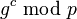$g^c \;\bmod\; p$ y lo envía a Alice.
Alice calcula $(g^c)^a \;\bmod\; p= g^{ca} \;\bmod\; p$ y lo envía a Bob.
Bob calcula 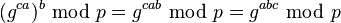$(g^{ca})^b \;\bmod\; p= g^{cab} \;\bmod\; p= g^{abc} \;\bmod\; p$ y lo usa como su clave secreta.

Cambiando de grupo

Podemos generalizar el protocolo y sus derivados si en lugar de basarnos en el grupo

\mathbf{Z}_{p}^{*}

nos basamos en otros grupos que cumplan las condiciones necesarias para poder aplicar el algoritmo (GDHP<-generalized diffie-hellman="" p="" problem="">

Formalización

Los usuarios A y B seleccionan públicamente un grupo multiplicativo finito G de orden n y generador 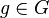$g \in G$ cuya operación multiplicación es una operación de una vía (no tiene inversa o difícilmente invertible)
El usuario A genera un número aleatorio a, 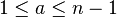$1 \le a \le n-1$ , calcula 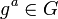$g^a \in G$ y transmite este elemento a B, manteniendo secreto a
El usuario B genera un número aleatorio b, 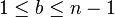$1 \le b \le n-1$ , calcula $g^b \in G$ y transmite este elemento a A, manteniendo secreto b
El usuario A recibe 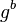$g^b$ y calcula $(g^b)^a \in G$
El usuario B recibe 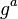$g^a$ y calcula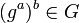 $(g^a)^b \in G$
A y B poseen un elemento común secreto del grupo $g^{a \cdot b}$

Ejemplos

Ejemplos de grupos que podríamos usar: El grupo multiplicativo análogo de los campos de Galois

\mathbb{F}_{2^{n}}

, el grupo de puntos definidos por una curva elíptica sobre un cuerpo finito.

Usos prácticos del protocolo

La red para anonimato Tor usa el protocolo Diffie Hellman, sobre una conexión TLS de una capa inferior previamente establecida, para procurarse claves de sesión entre el cliente y los nodos de enrutamiento de la red. Esas claves son usadas para cifrar las capas de cebolla de los paquetes que transitan por la red.
El protocolo Off-the-record messaging para comunicación de mensajería instantánea se apoya⁴ en el protocolo Diffie-Hellman para ir cambiando de clave de cifrado según se van intercambiando los mensajes.

El algoritmo de Diffie-Hellman

publicado por javier (Jul.22, 2011), en Seguridad

A veces pasa que vuelves a leer algo después de un tiempo y te sorprende como la primera vez. Me ha pasado con la explicación del algoritmo de Diffie-Hellman, utilizado aún hoy (es de 1976) como punto de partida de muchos protocolos de seguridad.

Esto lo escribí hace unos años, para una memoria.

El algoritmo de Diffie-Hellman (en honor a sus creadores, Whitfield Diffie y Martin Hellman) permite acordar una clave secreta entre dos máquinas, a través de un canal inseguro y enviando únicamente dos mensajes. La clave secreta resultante no puede ser descubierta por un atacante, aunque éste obtenga los dos mensajes enviados por el protocolo. La principal aplicación de este protocolo es acordar una clave simétrica con la que posteriormente cifrar las comunicaciones entre dos máquinas.

El protocolo de Diffie-Hellman fue publicado en 1976. Actualmente se conoce que es vulnerable a ataques de hombre en medio (MitM): un atacante podría situarse entre ambas máquinas y acordar una clave simétrica con cada una de las partes, haciéndose pasar por el host A de cara al host B y viceversa. Una vez establecidas las 2 claves simétricas, el atacante haría de puente entre los 2 hosts, descifrando toda la comunicación y volviéndola a cifrar para enviársela al otro host.

Para corregir la vulnerabilidad del protocolo, éste debe ser utilizado conjuntamente con algún sistema que autentique los mensajes. Esto ocurre, por ejemplo, durante el establecimiento de la asociación HIP, donde los paquetes R1 e I2, además de contener los mensajes de Diffie-Hellman, están firmados digitalmente.

En la figura siguiente se muestra un ejemplo de funcionamiento del protocolo Diffie-Hellman.

Los valores de “p” y “g” son públicos y cualquier atacante puede conocerlos, pero esto no supone una vulnerabilidad. Aunque un atacante conociese dichos valores y capturara los dos mensajes enviados entre las máquinas A y B, no sería capaz de averiguar la clave secreta. A continuación se muestra la información capturada por un atacante en el escenario de la Figura 46:

(g^a mod p) = 8 → (5^a mod 23) = 8
(g^b mod p) = 19 → (5^b mod 23) = 19

A partir de las ecuaciones anteriores, intentar calcular los valores de “a” y “b” es lo que se conoce como el problema del algoritmo discreto, un problema que se cree computacionalmente intratable y cuya notación es la siguiente:

a = log disc_g (g^a mod p) = log disc ₅ (8)
b = log disc_g (g^b mod p) = log disc ₅ (19)

Con los valores del ejemplo sí que es posible encontrar la solución, ya que se ha escogido un número primo “p” muy pequeño (p = 23), y se sabe que “a” y “b” son menores que “p”. Por lo tanto, para obtener los valores secretos en este ejemplo, un atacante tendría que probar sólo 22 posibles valores.

Por suerte, las implementaciones actuales del protocolo Diffie-Hellman utilizan números primos muy grandes, lo que impide a un atacante calcular los valores de “a” y “b”. El valor “g” no necesita ser grande, y en la práctica su valor es 2 ó 5. En el RFC 3526 aparecen publicados los números primos que deben utilizarse. A modo de ejemplo, se facilita aquí el número primo de 1024 bytes propuesto. El valor “g” utilizado es 2:

p = 2⁸¹⁹² – 2⁸¹²⁸ – 1 + 2⁶⁴ x ((2⁸⁰⁶² pi) + 4743158)

AMIGOS PARA SIEMPRE

Páginas

lunes, 26 de octubre de 2015

Criptografía

Algoritmos criptográficos

Métodos de construcción¹ ²

Basadas en aritmética modular

Basadas en cifradores de bloque

Funciones hash dedicadas

Ataques

Versión básica

Descripción detallada

Ataques

Ataques pasivos

Ataques activos

Ejemplo

Ejemplo con implementación de cifrado

Generalizaciones

Aumentando el número de partes

Cambiando de grupo

Formalización

Ejemplos

Usos prácticos del protocolo

El algoritmo de Diffie-Hellman

No hay comentarios:

Publicar un comentario

Datos personales

Archivo del blog

Páginas

lunes, 26 de octubre de 2015

Criptografía

Algoritmos criptográficos

Métodos de construcción1 2

Basadas en aritmética modular

Basadas en cifradores de bloque

Funciones hash dedicadas

Ataques

Versión básica

Descripción detallada

Ataques

Ataques pasivos

Ataques activos

Ejemplo

Ejemplo con implementación de cifrado

Generalizaciones

Aumentando el número de partes

Cambiando de grupo

Formalización

Ejemplos

Usos prácticos del protocolo

El algoritmo de Diffie-Hellman

No hay comentarios:

Publicar un comentario

Métodos de construcción¹ ²