Matemática financiera
análisis cuantitativo es la utilización de matemáticas financieras, con frecuencia derivadas de la física y de la estadística, para llevar a cabo análisis financiero. De modo similar, este tipo de análisis tiene lugar en la mayor parte de sectores industriales modernas, si bien en muchas ocasiones este análisis no se conoce en esos sectores como análisis cuantitativo. En la industria de inversión, los analistas que desarrollan análisis cuantitativo son conocidos normalmente como quants.
Aunque el área habitual de análisis de este tipo de técnicas era originalmente la gestión de activos, la gestión de riesgos y la fijación de precios de derivados financieros, el significado del término se ha expandido con el tiempo hasta incluir a aquellos individuos dedicados a casi cualquier aplicación de las matemáticas en finanzas. Entre los ejemplos se incluyen el arbitraje estadístico, el ''trading'' algorítmico y la realización de operaciones electrónicas en los mercados.
Historia
Las finanzas cuantitativas comenzaron en Estados Unidos en los años setenta, cuando algunos inversores comenzaron a utilizar fórmulas matemáticas para la asignación de precios de acciones y bonos.
Harry Markowitz, en su tesis de doctorado "Portfolio Selection" publicada en 1952, fue uno de los primeros en adaptar formalmente conceptos matemáticos a las finanzas. Markowitz formalizó una noción de rentabilidad media y de convarianzas para acciones que le permitió cuantificar el concepto de "diversificación" en un mercado. Mostró cómo procesar el retorno medio y la varianza para una cartera dada, y argumentó que los inversores deberían mantener solo aquellas carteras cuya varianza fuera mínima entre todas las carteras para un retorno medio dado.
En 1969, Robert Merton introdujo el cálculo estocástico en el estudio de las finanzas. Merton estaba motivado por el deseo de comprender cómo los precios son fijados en los mercados financieros, que es la cuestión económica clásica del "equilibrio".
En paralelo al trabajo de Merton y con su ayuda, Fischer Black y Myron Scholes desarrollaron el modelo Black–Scholes, que fue galardonado en 1997 con el Premio Nobel de Economía.
Acercamientos matemáticos y estadísticos
El análisis cuantitativo suele basarse en tres tipos de matemáticas: la estadística y la probabilidad, el cálculo centrado enecuaciones en derivadas parciales y la econometría. La mayoría de los analistas cuantitativos tienen escasa formación en economía, y suelen aplicar un conjunto de herramientas tomadas de la física. Los físicos suelen tener menos experiencia en técnicas estadísticas, por lo que suelen basarse en aproximaciones basadas en ecuaciones en derivadas parciales, y sus soluciones suelen basarse en el análisis numérico.
Los métodos numéricos más utilizados son:
- Método de las diferencias finitas, utilizado para resolver ecuaciones en derivadas parciales, y
- Método de Montecarlo, también utilizado para resolver ecuaciones en derivadas parciales, pero siendo también común la utilización de la simulación de Monte Carlo en la gestión de riesgos.
Análisis Cuantitativo de Pesonas Morales
En el caso de las personas morales, el análisis cuantitativo se basa en los estados de posición financiera (balance general, estado de resultados, estado de cambios en el capital y estado de flujo de efectivo).
Comunmente se realiza el análisis de forma vertical y horizontal.
El análisis vertical consiste en la evaluación de los estados financieros considerando un solo periodo, para ello es recomendable calcular diferentes razones financieras (de rentabilidad, de liquidez, de solvencia y de flujo).
El análisis horizontal se realiza comparando los estados financieros y sus razones entre varios periodos, a manera de poder identificar tendencias y situaciones de normalidad o extraordinarias.
También se realiza normalmente una comparación entre los resultados y razones financieras de la empresa evaluada respecto a otras que se ubiquen en el mismo sector y actividad, a modo de identificar aspectos positivos y negativos en la empresa que se está evaluando.
Hay otras maneras de evaluar cuantitativamente una persona moral con otro tipo de documentos e información, sin embargo, es mejor considerar todos los metodos como complementarios y no excluyentes.
Análisis Cuantitativo de Personas Físicas
El análsis cuantitativo de las personas físicas es por lo regular más complicado, ya que es muy facil conocer sus ingresos, pero sus gastos y su situación patrimonial no lo son tanto, y debe confiarse casi siempre en lo dicho por la persona en cuestión.
Para análizar los ingresos puede considerarse los recibos de nomina, declaraciones de impuestos o incluso estados de cuenta bancarios.
Como en el caso de las personas morales, cualquier metodo que se emplee es complementario a los demás.
Utilización del Conocimiento o Habilidad
Tuve la oportunidad de aplicar y mejorar estos conocimientos mediante el análisis de casos para efectos de otorgamiento de crédito y su seguimiento; el análisis del mismo banco y su cartera para efectos de reportar y dar explicaciones a la dirección, entidades regulatorias, auditores (externos e internos), calificadoras e incluso inversionistas; así como en el estudio de empresas en que el banco tenía interés de invertir o comprar completa o parcialmente.
Importancia
El análisis Cuantitativo es la base fundamental en el conocimiento de un negocio (en terminos financieros) y de un buen análisis de este aspecto puede dislumbrarse en que estado se encuentra.
Base o Base de cálculo a la convención que se pacta para calcular el número de días que han pasado para calcular el interés devengado en una operación financiera.
La base de cálculo es necesaria para evitar dudas respecto de los días pasados a computar para el cálculo de intereses. Por ejemplo, si se desea cancelar parte de unahipoteca en fecha 15 de febrero, respecto del mes anterior, ¿qué cálculo es el que se debe aplicar para obtener los intereses? ¿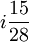 ? o ¿
? o ¿ , ya que se está a la mitad del mes?
, ya que se está a la mitad del mes?
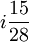 ? o ¿
? o ¿ , ya que se está a la mitad del mes?
, ya que se está a la mitad del mes?
Para una operación financiera pactada a un plazo total N, el interés devengado CC es el que resulta de calcular
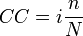
donde i es el tipo de interés y n es el número de días que han pasado desde el inicio de cálculo del pago de intereses.
Las convenciones más usadas en los mercados financieros son las siguientes: El numerador significa cómo se contarán los días del período devengado y el denominadorsignifica cómo se contarán los días del período total de pago de intereses.
- Base 30/360 : Todos los meses se computan como si tuvieran 30 días y los años como si tuvieran 360 días.
- Base 30/365 : Todos los meses se computan como si tuvieran 30 días y los años como si tuvieran 365 días.
- Base ACT/360: Todos los meses se computan por los días reales que tienen y los años como si tuvieran 360 días.
- Base ACT/365: Todos los meses se computan por los días reales que tienen y los años como si tuvieran 365 días.
- Base ACT/ACT: Todos los meses se computan por los días reales que tienen y los años por los días reales que tienen.
Los períodos inferiores a un mes siempre se cuentan por los días reales de calendario que han pasado.
Observaciones
Además de la base de cálculo hay convenciones que indican cómo considerar los días en el caso de que caigan en festivo y no se pueda realizar el pago. Se establecen entonces diferentes posibilidades a pactar:
- El siguiente día hábil sin modificar cálculo de n
- El día hábil anterior sin modificar el cálculo de n
- El siguiente día hábil modificando n hasta el día hábil siguiente
- El día hábil anterior modificando n hasta el día hábil anterior
Igualmente para operaciones a largo plazo, se suele pactar el calendario de festivos que regirá la operación. Por ejemplo, El calendario de Madrid, Barcelona, TARGET(el del sistema financiero europeo), etc.
Ejemplo
Si es 15 de junio de 2008 y se había pactado una operación desde el 15 de noviembre de 2007 al 15 de noviembre de 2008, el cálculo del coeficiente a aplicar sobre el tipo de interés por los días que faltan para terminar el año, seria:
- Base 30/360 = 210/360
- Base 30/365 = 210/365
- Base ACT/360= 213/360
- Base ACT/365= 213/365
- Base ACT/ACT= 213/366
Término utilizado en finanzas, bancos, títulos y valores financieros.
Un grado en una escala de 100 puntos, que se usa especialmente para expresar las variaciones que se producen en el rendimiento de bonos.
Por ejemplo, si el rendimiento de un bono cambia del 10.0 por ciento a 10.33 por ciento, se dice que aumentó en 33 puntos base.
curva cupón cero a la construida con los tipos de interés para diferentes plazos que cumplen la ecuación  que se corresponde con la cantidad a pagar (FC) por una unidad monetaria prestada hoy y devuelta en el momentot. Tanto el tipo de interés i como t se expresan en años. La inversa de FC es:
que se corresponde con la cantidad a pagar (FC) por una unidad monetaria prestada hoy y devuelta en el momentot. Tanto el tipo de interés i como t se expresan en años. La inversa de FC es:
 que se corresponde con la cantidad a pagar (FC) por una unidad monetaria prestada hoy y devuelta en el momentot. Tanto el tipo de interés i como t se expresan en años. La inversa de FC es:
que se corresponde con la cantidad a pagar (FC) por una unidad monetaria prestada hoy y devuelta en el momentot. Tanto el tipo de interés i como t se expresan en años. La inversa de FC es:
Los valores  se denominan factores de descuento.
se denominan factores de descuento.
 se denominan factores de descuento.
se denominan factores de descuento.
A diferencia de otros tipos de curvas de tipos de interés, por ejemplo la del euribor a 1 mes, 3 meses, etc. o la curva de tipos swap o la curva de rendimientos de bonos de gobiernos, no es una curva que sea observable directamente en los mercados financieros, especialmente para plazos superiores a un año.
Pero esta curva es muy importante ya que simplifica mucho el desarrollo y formulación matemática y el cálculo de valoración de todo tipo de instrumentos financieros.
A partir de diferentes curvas observables en el mercado (mercado monetario, swaps de tipos de interés, etc.) se construye la curva cupón cero. Se utilizan diferentes metodologías para su cálculo y, en especial, estimación para puntos no observables de la curva de tipos, como por ejemplo, el "bootstrapping".
Los valores del Estado suponen la referencia básica de la estructura temporal de los tipos de interés en España, y en cualquier país de corte occidental. Los bonos del Estado son instrumentos financieros con rendimiento explícito, esto es, pagan cupones periódicamente, lo que genera el denominado “riesgo de reinversión”, según el cual, cuando los bonos pagan un cupón, no se conoce el tipo de interés al que se podrá reinvertir a futuro, por lo que la inversión como tal se transforma más en una renta aleatoria, en términos de TIR, que en una renta cierta.
Por lo que antecede, en el mundo financiero, no se utiliza el TIR como instrumento de valoración, sino como instrumento de comparación estático, esto es, en un momento determinado. Ello significa que a la hora de evaluar la rentabilidad de una inversión, y para evitar el citado riesgo de reinversión, las entidades financieras utilicen los “tipos cupón cero” para valorar los flujos, esto es, tipos de interés desde la fecha de valoración hasta la fecha futura del flujo, sin pagos intermedios que provoquen la aleatoriedad de la reinversión.
Para obtener los tipos cupón cero, se parte de la cotización de los bonos del Estado en los mercados financieros a los distintos plazos, y a partir de la rentabilidad de dichos bonos, se construye un bono teórico sobre el cual se obtiene el tipo cupón cero al plazo correspondiente.
Veamos un ejemplo de aplicación, que es la forma más fácil de entender el mecanismo de generación de los tipos cupón cero.
Ejemplo: sabiendo que los tipos de interés (T.I.R.) de la deuda pública son: a 1 año (3,40%), a 2 años (3,65%), y a 3 años (3,80%), queremos obtener los tipos de interés de la curva cupón cero a tres años:
Tomamos el primer tipo (3,40%), y a partir de él, calculamos el segundo, imaginando un bono de precio 100 en origen, y que paga el tipo anual del 3,65% en dos años:
Análogamente:
de donde r3 = 3,808973 %.
Con los tipos “cupón cero” obtenidos, se conforma la curva “cupón cero”, que se correspondería con la gráfica temporal de la estructura de los tipos de interés.
Estos tipos son los que, por ejemplo, se utilizan en los mercados financieros para valorar flujos futuros, y en particular para valorar las coberturas de instrumentos derivados, los cuales constituyen operaciones sofisticadas que es preciso ajustar al máximo para evitar los riesgos de tipo de interés y de tipo de cambio.

No hay comentarios:
Publicar un comentario