Matemática financiera
cálculo variacional de Malliavin, nombrado así por Paul Malliavin, generaliza el cálculo de variaciones de funciones a procesos estocásticos. El cálculo variacional de Malliavin también se denomina cálculo variacional estocástico. En particular, permite definir la definción de la derivada de una variable aleatoria.
Las ideas de Malliavin llevaron a una demostración de que la condición de Hörmander implica la existencia de una densidad de probablidad suave para la solución de una ecuación diferencial estocástica. La demostración original de L. Hörmander se basaba en la teoría de ecuaciones en derivadas parciales. El cálculo de Malliavin ha sido aplicado también a las ecuaciones diferenciales estocásticas en derivadas parciales.
El cálculo de Malliavin permite definir la integración por partes de variables aleatorias, esta operación se usa en matemática financiera para calcular las sensibilidades de la derivada financiera. Además el cálculo de Malliavin ha encontrado algunas aplicaciones, por ejemplo, en el filtrado estocástico.
Panorama general e historia
El cálculo estocástico de Paul Malliavin generaliza como se ha dicho el cálculo de variaciones. Sólo que en lugar de resolver un problema variacional sobre un espacio de funciones lo hace sobre un espacio de procesos estocásticos
Principio de invariancia
El principio de invariancia usual para la integral de Lebesgue sobre la recta real es que, para cualquier número real ε y cualquier función integrable f, la siguiente condición se cumpla:
Esto puede usarse para deducir una fórmula de integración por partes, escogiendo f = gh y diferenciándloa con respecto a ε en ambos términos, lo que implica
Una idea parecida puede aplicarse en análisis estocástico para diferenciación a lo largo de una dirección de Cameron-Martin-Girsanov direction. De hecho, si 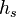 es un proceso predictile de cuadrado integrable y si se define:
es un proceso predictile de cuadrado integrable y si se define:
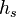 es un proceso predictile de cuadrado integrable y si se define:
es un proceso predictile de cuadrado integrable y si se define:
Siendo  un proceso de Wiener, el teorema de Girsanov entonces implica el siguiente análodo del principio de invariancia:
un proceso de Wiener, el teorema de Girsanov entonces implica el siguiente análodo del principio de invariancia:
 un proceso de Wiener, el teorema de Girsanov entonces implica el siguiente análodo del principio de invariancia:
un proceso de Wiener, el teorema de Girsanov entonces implica el siguiente análodo del principio de invariancia:
Diferenciando con respecto a ε en ambos miembros y evaluando en ε=0, se obtiene la siguiente fórmula de integración por partes:
Aquí, el término de la izquierda es la derivada de Malliavin de la variable aleatoria  en la dirección
en la dirección  y la integral que aparece a la derecha debe ser interpretada como una integral de Itō. Esta expresión también resulta cierta (por definición) si
y la integral que aparece a la derecha debe ser interpretada como una integral de Itō. Esta expresión también resulta cierta (por definición) si 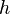 no está adaptado, dado que el miembro de la derecha se interpeta como una integral de Skorokhod.[cita requerida]
no está adaptado, dado que el miembro de la derecha se interpeta como una integral de Skorokhod.[cita requerida]
 en la dirección
en la dirección  y la integral que aparece a la derecha debe ser interpretada como una integral de Itō. Esta expresión también resulta cierta (por definición) si
y la integral que aparece a la derecha debe ser interpretada como una integral de Itō. Esta expresión también resulta cierta (por definición) si 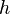 no está adaptado, dado que el miembro de la derecha se interpeta como una integral de Skorokhod.[cita requerida]
no está adaptado, dado que el miembro de la derecha se interpeta como una integral de Skorokhod.[cita requerida]Fórmula de Clark-Ocone
Uno de los resultados más útiles del cálculo variacional de Malliavin es el teorema de Clark-Ocone, que permite identificar explícitamente el proceso involucrado en elteorema de representación de martingalas. Una versión simple de este teorema afirma que:
|
Esto puede ser reexpresado de manera concisa mediante:
Mucho de trabajo en el desarrollo forma del cálculo variacional de Malliavin involucra extender este resultado a la clase más grande posible de funcionales F, reemplazando la derivada del núcleo usado anteriormente por la "derivada" de Malliavin denotada como  en la exposición del resultado anterior.
en la exposición del resultado anterior.
 en la exposición del resultado anterior.
en la exposición del resultado anterior.Intregral de Skorokhod
El operador integral de Skorokhod que se denota convencionalmente mediante δ se define como el operador adjunto de la derivada de Malliavin, así, para u en el dominio del operador (que es el un subjconjunto de  ), y para F en el dominio de la derivada de Malliavin se requiere que:
), y para F en el dominio de la derivada de Malliavin se requiere que:
 ), y para F en el dominio de la derivada de Malliavin se requiere que:
), y para F en el dominio de la derivada de Malliavin se requiere que:
donde el producto interno] es el definido en 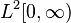 , es decir,
, es decir,
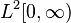 , es decir,
, es decir,
La existencia de este operador adjunto se sigue del teorema de representación de Riesz para operadores lineales sobre espacios de Hilbert. Se puede demostrarq que si uestá adaptada entonces
donde la integral debe entenderse en el sentido de Itō. Por tanto, esto proporciona una manera de extender la integral de Itō a integrandos no adaptados.
Aplicaciones
El cálculo de Malliavin permite la integración por partes en variables aleatorias, esta operación se usa en [[matemática fianciera para calcular la sensivilidad de la "derivada financiera" Además el cálculo tiene aplicaciones en el filtrado estocástico.
duración o duración de Macaulay, de un activo financiero compuestos de uno o varios flujos de caja, por ejemplo un bono, es la media ponderada de los distintos vencimientos de los flujos de caja, ponderados por el valor actual de cada uno de esos flujos. La duración mide también la sensibilidad del precio del activo al riesgo de tipo de interés. El concepto de duración fue desarrollo por Frederick Macaulay en 1938.
La compra de un bono proporciona distintos flujos de caja (cobros) a lo largo de la vida del título antes de ser amortizado. Para determinar la "duración" es necesario calcular el tiempo que transcurre hasta el pago de cada uno de los flujos de caja derivados de la compra del bono, ponderado por el valor presente del flujo conformado por el pago de cada cupón, ya que de acuerdo al tiempo en que sea pagado va a tener un tamaño diferente en el bono. Otra forma de entender la duración de un título es que la duración sería el plazo hasta el vencimiento de un bono cupón cero equivalente (un bono con un solo flujo de caja, en el que se devuelve el principal y los intereses de forma conjunta).
La fórmula que resulta es: ( VALOR PRESENTE DEL CUPÓN * TIEMPO DE PAGO DEL CUPÓN ) / PRECIO DEL BONO
Después de calcular el valor presente de los flujos se debe dividir por el precio del bono que no es más que la sumatorio de los valores presentes de los flujos de caja del bono. De esta forma se ha calculado finalmente la duración de Macaulay que por cierto es la base de otro cálculo de duración conocida como duración modificada.
El concepto de duración ha de englobarse dentro de la medida del riesgo de los títulos, si se comparan dos bonos que tienen el mismo plazo, es decir se amortizan a la vez, y el mismo rendimiento, pero en uno se pagan todos los intereses en el momento de la amortización (bono cupón cero) y en otro se van pagando los intereses a lo largo de la vida del título; el título cupón cero tiene un mayor riesgo de insolvencia y de variación de tipos de interés que el otro, esto introduce el concepto deduración, distinto de vencimiento o plazo de amortización. El concepto de duración ha reemplazado al concepto de madurez (plazo de tiempo hasta el vencimiento) como medida de la longitud de la corriente de pagos, porque la madurez mide exclusivamente el tiempo que transcurre hasta el último pago, sin tener en cuenta el momento y la cuantía del resto de los demás pagos. Por esto, la duración mide de manera mucho más precisa la longitud media del tiempo en la que se espera cobrar una inversión en bonos.
Ejemplo
Cálculo de la duración de un bono de 1.000€ de nominal que será amortizado a los tres años, otorga un cupón de 50 al año de la emisión, otro cupón de 50 a los dos años y en el tercer año se otorga otro cupón de 50 y a la vez será amortizado, tomando un tipo de actualización del 6%:
La duración de Macaulay será:
 años
años

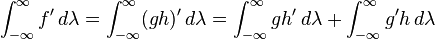
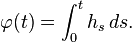
![\mathbb{E}(F(X + \varepsilon\varphi))= \mathbb{E} \left [F(X) \exp \left ( \varepsilon\int_0^1 h_s\, d X_s -
\frac{1}{2}\varepsilon^2 \int_0^1 h_s^2\, ds \right ) \right ]](https://upload.wikimedia.org/math/9/b/4/9b465f3ba6ea080ecf7f9af1d3fe69fc.png)
![\mathbb{E}(\langle DF(X), \varphi\rangle) = \mathbb{E}\Bigl[ F(X) \int_0^1 h_s\, dX_s\Bigr].](https://upload.wikimedia.org/math/f/2/6/f26461e799fc2ab2b708b002fffd0619.png)
![F: C[0,1] \to \R](https://upload.wikimedia.org/math/1/e/e/1ee24a4aab430be3208a1634d90f27f5.png) satisfaciendo
satisfaciendo  que sea
que sea 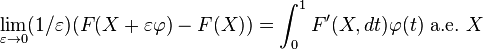





No hay comentarios:
Publicar un comentario