viernes, 23 de octubre de 2015

Magnitudes físicas


coeficiente de restitución (en realidad, cociente) es una medida del grado de conservación de la energía cinética en un choque entre partículas clásicas.

Introducción

En una colisión frontal alineada de dos esferas sólidas (como las que experimentan las bolas de billar) las velocidades después del choque están relacionadas con las velocidades antes del choque, por la expresión:
C_R = -\frac{V_{2f} - V_{1f}}{V_{2i} - V_{1i}}
Donde C_R es precisamente el coeficiente de restitución, que toma valores entre 0 y 1. El valor 1 se da en un choque perfectamente elástico, donde se conserva tanto elmomento lineal como la energía cinética del sistema. El valor 0\le C_R<1 se da en un choque inelástico (o plástico central) donde sólo se conserva el momento lineal, una porción de la energía cinética inicial de las partículas se "consume" durante el choque, convirtiéndose en energía de deformación plástica, energía sonora, calor, etcétera.
El coeficiente de restitución es la velocidad relativa de alejamiento, dividido entre la velocidad relativa de acercamiento de las partículas.

Expresiones analíticas

El coeficiente de restitución puede determinarse experimentalmente, en algunos pocos casos bajo ciertas hipótesis analíticas también puede calcularse teóricamente. Los cálculos teóricos prueban que el coeficiente depende de hecho de la velocidad de deformación (aunque frecuentemente este efecto se ignore), además del material del que estén hecho los cuerpos. La hipótesis más común consiste en suponer un material viscoelástico lineal. Para el caso de dos esferas del mismo material viscoelástico el coeficiente de restitución puede expresarse en potencias de la velocidad de aproximación:1
C_R = 1 - C_1\left(\frac{3}{2}A\right) \left(\frac{\rho}{m_{eff}}\right)^{2/5} v_r^{1/5} + C_2\left(\frac{3}{2}A\right)^2 \left(\frac{\rho}{m_{eff}}\right)^{4/5} v_r^{2/5} - \dots
Donde:
A = \frac{1}{3}\frac{(3\eta_2-\eta_1)^2}{3\eta_2+2\eta_1} \left[ \frac{(1-2\nu)(1-\nu^2)}{E\nu^2}\right]
\eta_1, \eta_2\,, constantes viscosas del material.
E, \nu\,, constantes elásticas del material: módulo de Young y coeficiente de Poisson.
\rho = \frac{2E}{3(1-\nu^2)}\sqrt{R_{eff}}
m_{eff} = m_1m_2/(m_1+m_2),\ R_{eff} = R_1R_2/(R_1+R_2),\,
R_i, m_i\,, radio y masa de la esfera i-ésima.
v_r = (\mathbf{v}_1-\mathbf{v}_2)\cdot \frac{(\mathbf{r}_1-\mathbf{r}_2)}{\|\mathbf{r}_1-\mathbf{r}_2\|}, velocidad relativa de aproximación.
C_1 = \frac{\sqrt{\pi}}{50^{1/5}} \frac{\Gamma(3/5)}{\Gamma(21/10)} = 1,15344,\ C_2 = 0,79826 constantes calculadas a partir de la ecuación de movimiento:
\begin{cases}\ddot{\xi} + \cfrac{\rho}{m_{eff}} \left( \xi^{3/2} + \cfrac{3}{2}A \sqrt{\xi}\dot{\xi} \right)\\ \xi(0) = 0, \dot{\xi}(0) = 0 \end{cases}
donde:
\xi = R_1 + R_2 -\|\mathbf{r}_1-\mathbf{r}_2\|, es la deformación por aplastamiento sufrida por la distancia entre centros de las dos esferas.

Aproximaciones

En el choque de una única partícula contra una superficie plana, es posible aplicar la aproximación de Servera-Galván.[cita requerida] A pesar de que este método permite reducir la complejidad de los cálculos, el resultado final sólo difiere ligeramente respecto la realidad.
C_R = \frac{\tan \varphi}{\tan \alpha}
En donde \alpha es el ángulo de la velocidad del centro de masas después del choque, y \varphi el ángulo de incidencia (ambos respecto a un eje paralelo a la superficie).
Fotografías de una pelota que rebota tomada con una luz estroboscópica a 25 imágenes por segundo. Si se desprecia la resistencia del aire, la raíz cuadrada de la relación de la altura de un rebote con respecto a la altura del rebote previo es el coeficiente de restitución del impacto pelota-superficie del suelo.


Coeficiente de restitución

Cuando dos cuerpos chocan, sus materiales pueden comportarse de distinta manera según las fuerzas de restitución que actúen sobre los mismos. Hay materiales cuyas fuerzas restituirán completamente la forma de los cuerpos sin haber cambio de forma ni energía cinética perdida en forma de calor, etc. En otros tipos de choque los materiales cambian su forma, liberan calor, etc., modificándose la energía cinética total.

Se define entonces un coeficiente de restitución (K) que evalúa esta pérdida o no de energía cinética, según las fuerzas de restitución y la elasticidad de los materiales.


Coeficiente de Restitución

V1(0), V2(0)  =   Velocidades de los cuerpos 1 y 2 antes del choque
V2(f), V1(f)   =   Velocidades de los cuerpos 1 y 2 después del choque



K es un número que varía entre 0 y 1. 

Si K = 0 choque perfectamente inelástico
Si 0
Si K = 1 choque perfectamente elástico











coeficiente de temperatura, habitualmente simbolizado como α, es una propiedad intensiva de los materiales que cuantifica la relación entre la variación de la propiedad física de un material y el cambio de temperatura. Por tanto, es el cambio relativo de una propiedad física cuando la temperatura se cambia un 1 K. Este coeficiente se expresa según el Sistema Internacional de Unidades en 1/K. Su expresión matemática toma la forma:
\alpha (T) =\frac{1}{R(T_0)} \cdot \frac{\partial R (T)}{\partial T}
donde:
  • α es el coeficiente de temperatura, que puede variar con la temperatura;
  • R (T) es la magnitud de la propiedad física del material a la temperatura T
  • R (T0) es la magnitud de la propiedad física del material a la temperatura de referencia T0
Si el coeficiente de temperatura es prácticamente constante en el intervalo de temperaturas entre T1 y T, es decir, la magnitud física depende linealmente de la temperatura, entonces puede realizarse la siguiente aproximación:
\alpha = \frac{1}{R(T_0)} \cdot \frac{\Delta R}{\Delta T} = \frac{1}{R(T_0)} \cdot \frac{R (T) - R (T_0)}{T - T_0}

En este caso, el coeficiente determina el aumento o disminución de la resistencia eléctrica de acuerdo con la variación de temperatura y la naturaleza de cada material. Este coeficiente se denomina con la letra α y se encuentra en la fórmula de la resistencia dependiendo del cambio de temperatura.
R = R_0\cdot(1+\alpha \cdot \Delta T)
Donde:
  • R : resistencia total
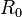  • R_0 : resistencia de referencia (a una temperatura fijada)
  • \alpha : el coeficiente en cuestión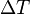
  • \Delta T : diferencia de T con respecto a una temperatura fijada


coeficiente de temperatura. [ing. temperature coefficient] El incremento relativo de la resistividad de los conductores por cada grado que aumenta su temperatura; es decir, . α es el coeficiente de temperatura, ρ la resistividad y T la temperatura absoluta del conductor. Se ve que la unidad del coeficiente de temperatura es el inverso del kelvin, es decir, K-1.













colorimetría es la ciencia que estudia la medida de los colores y que desarrolla métodos para la cuantificación del color, es decir la obtención de valores numéricos del color.

Procedimiento de la medida del color

Existe una necesidad de estandarizar el color para poderlo clasificar y reproducir. El procedimiento utilizado en la medida del color consiste sustancialmente en sumar la respuesta de estímulos de colores y su normalización a la curva espectral de respuesta del fotorreceptor sensible al color. Como referencia, se utiliza la curva espectral codificada de la Comisión Internacional de Iluminación, (conocida por sus siglas CIE en francés), la llamada función colorimétrica. Debe notarse que el color es una característica subjetiva, pues solo existe en el ojo y en el cerebro del observador humano, no siendo una característica propia de un objeto. Los fotorreceptores del ojo humano son los conos de la retina, de los que existen diferentes tipos, con sensibilidades diferentes a las distintas partes del espectro luminoso.
El matemático alemán Hermann Grassmann enunció unas leyes sobre la mezcla aditiva del color.1 Estas muestran que cualquier color puede expresarse como suma de tres colores primarios, es decir, de tres colores, cada uno de los cuales no puede obtenerse por la mezcla de los otros dos. Aplicando sus leyes, se obtiene la denominadaecuación unitaria del color, que representada, da una forma parecida a un triángulo, el triángulo internacional de color. El área dentro de las tres curvas que se obtienen con este procedimiento dan origen a tres valores: las coordinadas triestímulo X, Y y Z ligadas a las coordinadas de cromaticidad x e y por relaciones lineales. El paso de un espacio de colores a otro son datos de relaciones de transformación de coordenadas.

Percepción

El matiz es el estado puro del color: rojo, amarillo, azul... La saturación de un color es su grado de pureza. Un color está más saturado cuanto menor sea su contenido de grises o de blancos. Los colores de la naturaleza siempre son más o menos saturados. La intensidad, o luminosidad de un color, es la característica que hace que este aparezca más claro, independientemente de su saturación.

Evolución

Isaac Newton hizo un estudio sobre el color en su obra On colour (sobre el color).
La colorimetría ha tenido una gran expansión debido a la industria cosmética por el estudio de sombras, tintas, polvos y colores para el cabello. En la actualidad, otra importante expansión se ha debido a los problemas de gráficos por ordenador y a la reproducción de colores, así como por el análisis y la documentación de superficies antiguas, como cuadros y policromados. Utilizando técnicas para el análisis colorimétrico es posible llegar a un análisis químico del material superficial que se está analizando, como el análisis de la respuesta espectral.

La colorimetría es una técnica instrumental que tiene por objeto determinar la absorción de luz visible por una muestra, que puede ser una sustancia pura o bien una mezcla o disolución.
Para ello se utiliza un instrumento constituido por los siguientes elementos:
  • Fuente de radiación (luz blanca)
  • Sistema dispersivo (rendijas de entrada y salida, y red de difracción)
  • Detector (fototubo que transforma la señal luminosa en una señal eléctrica)  
  • Sistema de medida de la absorción, una vez amplificada (convertidor analógico o digital).
Uno de los instrumentos más utilizados es el modelo “Spectronic 20” diseñado en 1952
por Bausch – Lomb,
y que con algunos perfeccionamientos se sigue fabricando en la actualidad.
La absorción de radiación por una muestra en la región visible, así como en general en cualquier región del espectro, está regida por la ley de Lambert – Beer. Esta ley establece que la fracción de luz absorbida por una muestra es tanto mayor cuanto más grande es el número de moléculas sobre las que incide la radiación
Publicado por en

No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)