coeficiente de dilatación es el cociente que mide el cambio relativo de longitud o volumen que se produce cuando un cuerpo sólido o un fluido dentro de un recipiente cambia de temperatura provocando una dilatación térmica.
De forma general, durante una transferencia de calor, la energía que está almacenada en los enlaces intermoleculares entre dosátomos cambia . Cuando la energía almacenada aumenta, también lo hace la longitud de estos enlaces. Así, los sólidos normalmente se expanden al calentarse y se contraen al enfriarse;1 este comportamiento de respuesta ante la temperatura se expresa mediante elcoeficiente de dilatación térmica (típicamente expresado en unidades de °C-1):
Sólidos
Para los sólidos, el tipo de coeficiente de dilatación más comúnmente usado es el coeficiente de dilatación lineal αL. Para una dimensión lineal cualquiera, se puede medir experimentalmente comparando el valor de dicha magnitud antes y después de cierto cambio de temperatura, como:
Puede ser usada para abreviar este coeficiente, tanto la letra griega alfa  como la letra lambda
como la letra lambda  .
.
 como la letra lambda
como la letra lambda  .
.Térmica
Dilatación, por lo general, la materia se dilata al calentar y se contrae al enfriarla. Esta dilatación se supone que "a" no depende de la temperatura lo cual no es estrictamente cierto.Se denomina dilatación térmica al aumento de longitud, volumen o alguna otra dimensión métrica que sufre un cuerpo físico debido al aumento de temperatura que se provoca en él por cualquier medio.
Gases y líquidos
En gases y líquidos es más común usar el coeficiente de dilatación volumétrico  o
o  , que viene dado por la expresión:
, que viene dado por la expresión:
 o
o  , que viene dado por la expresión:
, que viene dado por la expresión:
Para sólidos, también puede medirse la dilatación térmica, aunque resulta menos importante en la mayoría de aplicaciones técnicas. A partir del cálculo se deduce que el coeficiente de dilatación volumétrico es el triple del coeficiente de dilatación lineal, por lo tanto, para los rangos donde el coeficiente es constante se cumple:
| Glicerina | 0.51 x 10-3 |
| Mercurio | 0.18 x 10-3 |
| Agua | 0.21 x 10-3 |
Nota: La unidad del SI (Sistema Internacional) es el Kelvin (K-1), aunque como se trata de variaciones, esto no afecta los cálculos.
Aplicaciones
El conocimiento del coeficiente de dilatación lineal adquiere una gran importancia técnica en muchas áreas del diseño industrial. Un buen ejemplo son los rieles del ferrocarril; estos van soldados unos con otros, por lo que pueden llegar a tener una longitud de varios centenares de metros. Si la temperatura aumenta mucho la vía férrea se desplazaría por efecto de la dilatación, deformando completamente el trazado. Para evitar esto, se estira el carril artificialmente, tantos centímetros como si fuese una dilatación natural y se corta el sobrante, para volver a soldarlo. A este proceso se le conoce como neutralización de tensiones.
Para ello, cogeremos la temperatura media en la zona y le restaremos la que tengamos en ese momento en el carril; el resultado lo multiplicaremos por el coeficiente de dilatación del acero y por la longitud de la vía a neutralizar...
Valores del coeficiente de dilatación lineal
| Material | α (°C-1) |
|---|---|
| Hormigón | 1.2 x 10-5 |
| Acero | 1.2 x 10-5 |
| Hierro | 1.2 x 10-5 |
| Plata | 3.0 x 10-5 |
| Oro | 1.5 x 10-5 |
| Invar | 0,04 x 10-5 |
| Plomo | 3.0 x 10-5 |
| Zinc | 2.6 x 10-5 |
| Aluminio | 2.4 x 10-5 |
| Latón | 1.8 x 10-5 |
| Cobre | 1.7 x 10-5 |
| Vidrio | 0.7 a 0.9 x 10-5 |
| Cuarzo | 0.04 x 10-5 |
| Hielo | 5.1 x 10-5 |
| Diamante | 0.12 x 10-5 |
| Grafito | 0.79 x 10-5 |

coeficiente de película o coeficiente de convección, representado habitualmente como h, cuantifica la influencia de las propiedades del fluido, de la superficie y del flujo cuando se produce transferencia de calor por convección.

donde  es el coeficiente de película,
es el coeficiente de película,  es el área del cuerpo en contacto con el fluido,
es el área del cuerpo en contacto con el fluido,  es la temperatura en la superficie del cuerpo y
es la temperatura en la superficie del cuerpo y  es la temperatura del fluido lejos del cuerpo.
es la temperatura del fluido lejos del cuerpo.
 es el coeficiente de película,
es el coeficiente de película,  es el área del cuerpo en contacto con el fluido,
es el área del cuerpo en contacto con el fluido,  es la temperatura en la superficie del cuerpo y
es la temperatura en la superficie del cuerpo y  es la temperatura del fluido lejos del cuerpo.
es la temperatura del fluido lejos del cuerpo.
El coeficiente de convección depende de múltiples parámetros relacionados con el flujo del fluido a través del cual se da la convección:
- del tipo de convección (forzada o natural)
- del régimen del fluido (laminar o turbulento)
- de la velocidad del flujo
- de la viscosidad del fluido,
- de la densidad del fluido,
- de la conductividad térmica del fluido,
- del calor específico del fluido.
- del coeficiente de dilatación del fluido,
- de la forma de la superficie de intercambio
- de la rugosidad de la superficie de intercambio
- de su temperatura,
- de si el derrame es interior o exterior,...
Las formas clásicas de estimarlo se basan en el empleo de correlaciones de números adimensionales (vid. número de Nusselt), de manera que en general se dispone de una igualdad entre el número de Nusselt, que es proporcional al coeficiente de convección, y una cierta expresión que involucra al número de Reynolds y al número de Prandtl en convección forzada, y al de Prandtl y al número de Grashof en convección natural.
Otras formas de calcularlo se basarían en emplear modernos programas de diferencias finitas para resolver las ecuaciones de Navier-Stokes numericamente, siendo esta última opción muy costosa en terminos computacionales.
coeficiente de Poisson (denotado mediante la letra griega 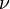 ) es una constante elástica que proporciona una medida del estrechamiento de sección de un prisma de material elástico lineal e isótropo cuando se estira longitudinalmente y se adelgaza en las direcciones perpendiculares a la de estiramiento. El nombre de dicho coeficiente se le dio en honor al físico francés Simeon Poisson.
) es una constante elástica que proporciona una medida del estrechamiento de sección de un prisma de material elástico lineal e isótropo cuando se estira longitudinalmente y se adelgaza en las direcciones perpendiculares a la de estiramiento. El nombre de dicho coeficiente se le dio en honor al físico francés Simeon Poisson.
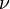 ) es una constante elástica que proporciona una medida del estrechamiento de sección de un prisma de material elástico lineal e isótropo cuando se estira longitudinalmente y se adelgaza en las direcciones perpendiculares a la de estiramiento. El nombre de dicho coeficiente se le dio en honor al físico francés Simeon Poisson.
) es una constante elástica que proporciona una medida del estrechamiento de sección de un prisma de material elástico lineal e isótropo cuando se estira longitudinalmente y se adelgaza en las direcciones perpendiculares a la de estiramiento. El nombre de dicho coeficiente se le dio en honor al físico francés Simeon Poisson.Materiales isótropos
Si se toma un prisma mecánico fabricado en el material cuyo coeficiente de Poisson pretendemos medir y se somete este prisma a una fuerza de tracción aplicada sobre sus bases superior e inferior, el coeficiente de Poisson se puede medir como: la razón entre el alargamiento longitudinal producido dividido por el acortamiento de una longitud situada en un plano perpendicular a la dirección de la carga aplicada. Este valor coincide igualmente con el cociente de deformaciones, de hecho la fórmula usual para el Coeficiente de Poisson es:
Donde ε es la deformación.
Para un material isótropo elástico perfectamente incompresible, este es igual a 0,5. La mayor parte de los materiales prácticos en la ingeniería rondan entre 0,0 y 0,5, aunque existen algunos materiales compuestos llamados materiales augéticos que tienen coeficiente de Poisson negativo. Termodinámicamente puede probarse que todo material tiene coeficientes de Poisson en el intervalo (-1, 0,5), dado que la energía elástica de deformación (por unidad de volumen) para cualquier material isótropo alrededor del punto de equilibrio (estado natural) puede escribirse aproximadamente como:
La existencia de un mínimo relativo de la energía para ese estado de equilibrio requiere:
Esta última condición sólo se puede cumplir si el coeficente de Poisson cumple 

Ley de Hooke generalizada
Conociendo lo anterior se puede concluir que al deformarse un material en una dirección producirá deformaciones sobre los demás ejes, lo que a su vez producirá esfuerzos en todos lo ejes. Por lo que es posible generalizar la ley de Hooke como:
Materiales ortótropos
Para materiales ortotrópicos (como la madera), el cociente entre la deformación unitaria longitudinal y la deformación unitaria transversal depende de la dirección de estiramiento, puede comprobarse que para un material ortotrópico el coeficiente de Poisson aparente puede expresarse en función de los coeficientes de Poisson asociados a tres direcciones mutuamente perpendiculares. De hecho entre las 12 constantes elásticas habituales que definen el comportamiento de un material elástico ortotrópico, sólo 9 de ellas son independientes ya que deben cumplirse las restricciones entre los coeficientes de Poisson principales y los módulos de Young principales:
Valores para varios materiales
El coeficiente de Poisson es adimensional. Para ver el valor del coeficiente de Poisson para varios materiales consultar los valores del coeficiente de Poisson delAnexo:Constantes elásticas de diferentes materiales.
Enlaces externos
- (Inglés) Materiales Augéticos
| [ocultar]Fórmulas de conversión | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Los materiales elásticos lineales isótropos homogéneos tienen sus propiedades elásticas únicamente determinadas por dos módulos cualesquiera de los especificados anteriormente, por lo tanto, cualquier otro módulo de elasticidad puede ser calculado de acuerdo a estas fórmulas. | ||||||||||
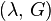 |  |  |  |  |  | 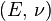 | 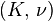 |  |  | |
 | 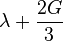 |  | 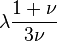 |  |  |  | ||||
 | 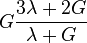 | 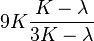 |  |  |  |  | 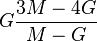 | |||
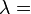 |  |  |  | 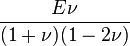 |  | 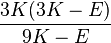 |  | |||
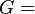 |  | 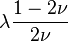 | 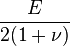 | 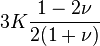 | 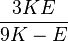 | |||||
 | 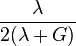 |  |  |  | 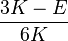 |  | ||||
 | 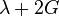 |  | 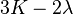 |  |  | 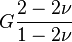 |  | |||
El coeficiente de Poisson (n) es un parámetro característico de cada material que indica la relación entre las deformaciones longitudinales que sufre el material en sentido perpendicular a la fuerza aplicada y las deformaciones longitudinales en dirección de la fuerza aplicada sobre el mismo. Así, si sobre el cuerpo de la figura se aplica una fuerza de tracción en dirección x se produce un alargamiento relativo ex en esa dirección y un acortamiento relativo ey y ez en las dos direcciones transversales, definiéndose el coeficiente de Poisson como:




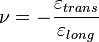


![\begin{cases}
\varepsilon_x = \cfrac {1}{E}
\left[ \sigma_x - \nu \left( \sigma_y + \sigma_z \right) \right] \\
\varepsilon_y = \cfrac {1}{E}
\left[ \sigma_y - \nu \left( \sigma_x + \sigma_z \right) \right] \\
\varepsilon_z = \cfrac {1}{E}
\left[ \sigma_z - \nu \left( \sigma_x + \sigma_y \right) \right] \end{cases}](https://upload.wikimedia.org/math/3/a/3/3a36ebb011815d396533edcbf118aafc.png)

No hay comentarios:
Publicar un comentario