AMIGOS PARA SIEMPRE: Teorías matemáticas

Teoría de cuerpos

teoría de Galois es una colección de resultados que conectan la teoría de cuerpos con la teoría de grupos. La teoría de Galois tiene aplicación a diversos problemas de la teoría de cuerpos, y que gracias a este desarrollo, pueden ser reducidos a problemas más sencillos de la teoría de grupos. La teoría de Galois debe su nombre al matemático francés Évariste Galois (1811-1832), fallecido a la edad de 20 años.

Aplicaciones de la teoría de Galois

El nacimiento de la teoría de Galois estuvo motivada por el intento de responder a la siguiente cuestión:

¿Por qué no existe una fórmula para la resolución de ecuaciones polinómicas de quinto grado (o superior) en términos de los coeficientes del polinomio, usando operaciones algebraicas (suma, resta, multiplicación, división) y la extracción de raíces (raíces cuadradas, cúbicas, etc); tal como existe para las ecuaciones de segundo, tercer y cuarto grado?

El teorema de Abel-Ruffini que es parte de la teoría de Galois, da una respuesta a esta pregunta. La teoría de Galois proporciona no sólo una elegante respuesta a esta cuestión, sino que también explica en detalle por qué es posible resolver ecuaciones de grado inferior al quinto, y por qué las soluciones son expresables mediante operaciones algebraicas y extracción de raíces.

Además la teoría de Galois proporciona respuestas a problemas clásicos de la constructibilidad mediante regla y compás. De hecho, la teoría de Galois establece cuándo es posible construir una cierta longitud proporcional a una dada, y gracias a eso pueden responderse a las siguientes preguntas:

¿Qué polígonos regulares son construibles mediante regla y compás?

¿Por qué no es posible la trisección de un ángulo?

El enfoque de la teoría de Galois usando el grupo de permutaciones

Si tenemos un polinomio puede suceder que algunas de sus raíces estén digamos que "conectadas" mediante varias ecuaciones algebraicas, que cumplan dichas raíces. Por ejemplo, puede suceder que para dos de las raíces, digamos A y B, la ecuación A² + 5B³ = 7 sea cierta. La idea central de la teoría de Galois es el considerar aquellas permutaciones (o arreglos) de las raíces que tengan la propiedad de que cualquier ecuación algebraica satisfecha por ellas sea satisfecha también tras la permutación o el arreglo. Es importante señalar que nos restringimos a ecuaciones algebraicas cuyos coeficientes son números racionales. (Se pueden especificar ciertoscuerpos para los coeficientes, pero en los ejemplos de abajo serán los números racionales los que usemos.)

El conjunto de tales permutaciones formarán un grupo de permutaciones, también llamado Grupo de Galois del polinomio (sobre los números racionales). Un ejemplo:

Primer ejemplo: ecuación cuadrática

Sea la ecuación cuadrática

x^2 -4x +1 = 0

Mediante el uso de la fórmula para la ecuación cuadrática sabemos que sus dos raíces son

A = 2 + \sqrt{3}

B = 2 - \sqrt{3}

Algunas de las ecuaciones algebraicas que satisfacen A y B son

A+B=4

AB=1

En cada una de estas ecuaciones es claro que si intercambiamos los papeles de A y B obtenemos ecuaciones válidas. Pero además esto es cierto, aunque menos obvio, para cualquier ecuación algebraica que satisfacen A y B. Para probarlo se requiere de la teoría de los polinomios simétricos.

Concluimos que el grupo de Galois del polinomio

x^2 -4x +1

consiste en dos permutaciones: la identidad que deja A y B quietas, y la transposición, que intercambia A y B. Como grupo, es isomorfo al grupo cíclico de orden dos, denotado Z/2Z.

Podríamos plantear la objeción de que existe esta otra ecuación satisfecha por A y B:

A-B-2 \sqrt{3} =0

pero que no es cierta cuando intercambiamos los papeles. Sin embargo hemos de observar que no nos importa pues sus coeficientes no son racionales;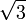

\sqrt{3}

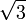es irracional.

De forma parecida podemos hablar de cualquier polinomio cuadrático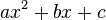

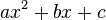ax^2+bx+c

, donde a, b y c son números racionales.

Si el polinomio tiene sólo una raíz, por ejemplo $x^2 -4x +4 = (x-2)^2$ , entonces el grupo de Galois es trivial; esto es, contiene sólo a la permutación identidad.
Si tiene dos distintas raíces racionales, por ejemplo $x^2 -3x +2 = (x-2)(x-1)$ , el grupo es de nuevo trivial.
Si tiene dos raíces irracionales (inclusive el caso en el que ambas son números complejos), entonces el grupo de Galois contiene dos permutaciones, como en el ejemplo anterior.

Segundo ejemplo

Considérese el siguiente polinomio:

x^4 -10x^2 +1

que puede escribirse también como:

(x^2 -5)^2 -24

Deseamos describir el grupo de Galois de este polinomio, nuevamente sobre el cuerpo de los números racionales. El polinomio tiene cuatro raíces:

A = \sqrt{2} + \sqrt{3}

B = \sqrt{2} - \sqrt{3}

C = -\sqrt{2} + \sqrt{3}

D = -\sqrt{2} - \sqrt{3}.

Existen 4! = 24 maneras de permutar estas cuatro raíces, pero no todas estas permutaciones son miembros del grupo de Galois. Los miembros del grupo de Galois debe preservar cualquier ecuación algebraica con coeficientes racionales A, B, C y D. Una de dichas ecuaciones es por ejemplo:

A+D=0

Ya que puesto que

A + C = 2\sqrt{3} \neq 0

la permutación

(A, B, C, D) → (A, B, D, C)

no está permitda, porque transforma la ecuación válida A + D = 0 en la ecuación inválida A + C = 0.

Otra ecuación que las raíces satisfacen es:

(A+B)^2 =8

Esto excluiría más permutaciones, como por ejemplo:

(A, B, C, D) → (A, C, B, D).

Continuando de esta manera, podemos encontrar que sólo las permutaciones que satisfacen las dos ecuaciones anteriores simultáneamente son:

(A, B, C, D) → (A, B, C, D)

(A, B, C, D) → (C, D, A, B)

(A, B, C, D) → (B, A, D, C)

(A, B, C, D) → (D, C, B, A),

y por tanto el grupo de Galois es isomorfo al grupo de Klein.

Grupos solubles y solución por radicales

Se dice que una raíz α se puede expresar en radicales si α es elemento de un cuerpo K tal que

F = K_0 \subset K_1 \subset \cdots \subset K_s = K

donde

K_{i+1} = K_i(\sqrt[n_i]{a_i}) \,\exists\, a_i \in K_i, i = 0, 1, \ldots, s-i

. Una ecuación polinomial es soluble por radicales si todas sus raíces se pueden expresar en radicales.¹ Con la teoría de Galois podemos derivar el siguiente teorema:

El polinomio f(x) (en el cuerpo F) es soluble por radicales si y sólo si su grupo de Galois essoluble.²

El problema inverso de Galois

El problema inverso de Galois plantea si todo grupo finito puede ser el grupo de Galois de alguna extensión de los números racionales. Este problema, propuesto inicialmente en el siglo XIX por Hilbert, permanece sin resolver.

Es por todos conocidas y, de hecho, es una de las fórmulas matemáticas que permanece en la memoria para toda la vida aunque uno se desvincule de las matemáticas para siempre, las soluciones de la ecuación de segundo grado ax² + bx + c = 0

$x=\frac{-b \pm \sqrt {b^2-4ac\ }}{2a}.$

Ahora bien, ya no son tan conocidas las soluciones de la ecuación de tercer grado ax³ + bx² + cx + d = 0, cuyas fórmulas son bastante grandes (pincharaquí para verlas, no asustarse) y sólo se estudian en cursos avanzados de matemáticas.

Si nos vamos a la ecuación de cuarto grado ax⁴ + bx³ + cx² + dx + e = 0 , la complejidad aumenta considerablemente (ver aquí las soluciones).

Como vemos en estas enrevesadas fórmulas, todas se basan en que hay que aplicar únicamente un número finito de sumas, restas, multiplicaciones, divisiones y raíces con los coeficientes de la ecuación. El éxito obtenido con estas ecuaciones de hasta cuarto grado parece augurar que todas las ecuaciones van a tener soluciones reales, complicadas eso sí, pero soluciones. Pues no. El teorema de Abel o teorema de Abel-Ruffini postula que no puede resolverse por radicales las ecuaciones polinómicas generales de grado igual o superior a cinco. Es decir, no es posible encontrar las soluciones de la ecuación general:

Évariste Galois

$a_n x^n + a_{n - 1} x^{n - 1} + \cdots + a_1 x + a_0 = 0,$

con n superior o igual a cinco.

El teorema no afirma que las ecuaciones polinómicas de grado cinco o superior no tengan soluciones o que no puedan ser resueltas. El contenido del teorema es que la solución de una ecuación de grado cinco o superior no puede siempre ser expresada comenzando por los coeficientes y usando sólo sumas, restas, multiplicaciones, divisiones y raíces con los coeficientes de la ecuación. El criterio preciso que separa aquellas ecuaciones que pueden ser resueltas mediante radicales de aquellas que no fue dado por Évariste Galois, del que ahora se ha cumplido el segundo centenario de su nacimiento el 25 de octubre de 1811, un matemático francés que en su corta vida (21 años) se reveló como un gran genio, haciendo aportaciones de primer orden como ésta.

teorema fundamental de la teoría de Galois es un resultado que describe la estructura de ciertos tipos de extensiones de cuerpos.

En su forma más básica el teorema dice que dada una extensión de cuerpos E/F que sea finita y Galois, existe una correspondencia uno a uno entre sus cuerpos intermedios (cuerpos K que satisfacen F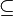

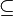\subseteq

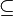\subseteq

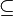E; también llamados subextensiones de E/F) y los subgrupos de su grupo de Galois.

Descripción explícita de la correspondencia

Para extensiones finitas, la correspondencia puede describirse explícitamente como sigue:

Para cada subgrupo H de Gal(E/F), el cuerpo correspondiente, denotado normalmente E^H, es el conjunto de aquellos elementos de E que son fijos para cada automorfismo en H.
Para cada cuerpo intermedio K de E/F, el subgrupo correspondiente es precisamente Aut(E/K), esto es, el conjunto de aquellos automorfismos en Gal(E/F) que dejan fijo a cada elemento de K.

Por ejemplo, el cuerpo más "grande" E se corresponde al subgrupo trivial de Gal(E/F), y el cuerpo base F se corresponde al grupo completo: Gal(E/F).

Propiedades de la correspondencia

La correspondencia tiene las siguientes propiedades útiles:

Es revertible por inclusión. La inclusión de subgrupos H₁ $\subseteq$ H₂ se da si y sólo si se da también la inclusión en cuerpos: E^H₁ $\supseteq$ E^H₂.
Los grados de las extensiones están relacionados con el orden de los grupos de manera consistente con la propiedad anterior. Concretamente, si H es un subgrupo de Gal(E/F), entonces |H| = [E:E^H] y [Gal(E/F):H] = [E^H:F].
El cuerpo E^H es una extensión normal de F si y sólo si H es un subgrupo normal de Gal(E/F). En este caso, la restricción de los elementos de Gal(E/F) al E^Hinduce un isomorfismo entre Gal(E^H/F) y el grupo cociente Gal(E/F)/H.

Aplicaciones

El teorema transforma el problema de clasificar los cuerpos intermedios de E/F en el problema menos difícil de listar los subgrupos de cierto grupo finito.

Por ejemplo, para demostrar que la ecuación general de quinto grado no es resoluble por radicales (ver teorema de Abel-Ruffini), se debe establecer el problema en términos de extensiones radicales (extensiones de la forma F(α) donde α es una n-sima raíz de algún elemento de F), y entonces usar el teorema fundamental para convertir esta afirmación en un problema sobre grupos que ya podamos atacar más directamente.

Las teorías como Teoría de Kummer y la teoría de cuerpos de clases se derivan del teorema fundamental.

Caso infinito

Existe también una versión de este teorema fundamental de la teoría de Galois que se aplica a extensiones algebraicas infinitas, que además son normales y separables. Se requiere para ello definir una cierta estructura topológica, la Topología de Krull sobre el grupo de Galois; entonces sólo aquellos subgrupos que sean tambiéncerrados de la topología serán relevantes para la correspondencia del teorema.

extensión de Galois (o extensión galoisiana) si es una extensión normal y separable. En este caso, se puede considerar el grupo de Galois de la extensión y sobre él es válida la tesis del Teorema Fundamental de la Teoría de Galois.

Definición

Sea la extensión E sobre un cuerpo base K (E/K).

Por ser normal, E es el cuerpo de descomposición de un polinomio con coeficientes en K; o, equivalentemente, las K-inmersiones de E en un cuerpo algebraicamente cerrado que contenga a K son automorfismos de E sobre K.
Por ser separable, dicho polinomio descompone completamente en raíces simples.

Grupo de Galois

Sobre una extensión de Galois E/K, se define el grupo de Galois Gal(E/K) como el grupo de los automorfismos de E sobre K. Por ser E/K normal, toda K-inmersión entre E y Ω es un automorfismo y se tiene:

\operatorname{Gal}(E/K)=\operatorname{Aut}_K(E)=\lbrace\sigma : E\rightarrow\bar K : \sigma \mbox{ } K \mbox{-}\mathrm{inmersi\acute on}\rbrace

siendo el cardinal del grupo

|\operatorname{Gal}(E/K)|=|\operatorname{Aut}_K(E)|=\lbrack E:K\rbrack

grupo de Galois es un grupo asociado a un cierto tipo de extensión de cuerpo. El estudio de las extensiones de cuerpos (y los polinomios que dan lugar a ellas) mediante el grupo de Galois es conocido como teoría de Galois.

Para ver una discusión más elemental de los grupos de Galois en términos de los grupos de permutaciones, ver el artículo sobre teoría de Galois .

Definición de grupo de Galois

Supongamos que E es una extensión del cuerpo F. Consideremos el conjunto de todos los automorfismos de cuerpos de E/F; esto es, los isomorfismos α de E a sí mismo, tal que α(x) = x para cada x en F. Este conjunto de automorfismos junto con la operación de composición de funciones forma un grupo G, denotado habitualmente Aut(E/F) o

\operatorname{Aut}_{F} E

Si E/F es una extensión de Galois, entonces G es llamado el grupo de Galois de la extensión, y se denota normalmente Gal(E/F). La importancia de que una extensión sea de Galois se debe a que obedece al teorema fundamental de la teoría de Galois.

Se puede demostrar que E es algebraico sobre F si y sólo si el grupo de Galois es profinito.

Ejemplos

En los siguientes casos F es un cuerpo, y C, R, Q son los cuerpos de los números complejos, reales, y racionales, respectivamente. La notación F(a) indica la extensión de cuerpo obtenida por unión de un elemento a al cuerpo F.

Gal(F/F) es el grupo trivial que tiene un solo elemento, llamado el automorfismo identidad.
Gal(C/R) tiene dos elementos, el automorfismo identidad y el automorfismo de conjugación compleja.
Aut(R/Q) es trivial. En efecto, se puede mostar que cualquier Q-automorfismo debe preservar el orden de los números reales y por lo tanto debe ser la identidad.
Aut(C/Q) es un grupo infinito.
Gal(Q(√2)/Q) tiene dos elementos, el automorfismo identidad y el automorfismo el cual intercambia √2 y −√2.
Considérese el cuerpo K = Q(³√2). El grupo Aut(K/Q) contiene únicamente el automorfismo identidad. Esto es porque K no es un extensión normal, puesto que las otras dos raíces cúbicas de 2 (ambas complejas) no se encuentran en la extensión — en otras palabras, K no es un cuerpo de descomposición.
Considérese ahora L = Q(³√2, ω), donde ω es la tercera raíz primitiva de la unidad. El grupo Gal(L/Q) es isomorfo a S₃, el grupo diédrico de orden 6, y L es, en efecto, el cuerpo de descomposición de x³ − 2 sobre Q.
Si q es una potencia prima, y si F = GF(q) y E = GF(qⁿ) denota el cuerpos de Galois de orden q y qⁿ respectivamente, entonces Gal(E/F) es cíclico de orden n.
Si f es un polinomio irreducible de grado primo p con coeficientes racionales y exactamente con dos raíces no reales, entonces el Grupo de Galois de f es el grupo simétrico completoS_p.

Propiedades

La importancia de una extensión que Galois es que obedece al teorema fundamental de la teoría de Galois: los subgrupos cerrados (con respecto a la topología de Krull mostrada abajo) del grupo de Galois corresponden a cuerpos intermedios de una extensión de cuerpos.

Si E/F es una extensión de Galois, entonces Gal(E/F) puede ser dada una topología, llamada topología de Krull, que lo convierte en un grupo profinito.

AMIGOS PARA SIEMPRE

Páginas

jueves, 22 de octubre de 2015

Teorías matemáticas