Teoría de cuerpos
cuerpo o campo es una estructura algebraica en la cual las operaciones llamadas adición y multiplicación se pueden realizar y cumplen las propiedades: asociativa, conmutativa y distributiva de la multiplicación respecto de la adición,1 además de la existencia de inverso aditivo, de inverso multiplicativo y de un elemento neutro para la adición y otro para la multiplicación, los cuales permiten efectuar las operaciones de sustracción y división (excepto la división por cero); estas propiedades ya son familiares de la aritmética de números ordinarios.
Los cuerpos son estructuras algebraicas importantes de estudio en diversas ramas de la matemática: álgebra, análisis matemático, teoría de los números, puesto que proporcionan la generalización apropiada de dominios de números tales como los conjuntos de números racionales, de los números reales, o de los números complejos. Los cuerpos eran llamados dominios racionales.
El concepto de un cuerpo se usa, por ejemplo, al definir el concepto de espacio vectorial y las transformaciones en estos objetos, dadas por matrices, dos objetos en elálgebra lineal cuyos componentes pueden ser elementos de un cuerpo arbitrario. La teoría de Galois estudia las relaciones de simetría en las ecuaciones algebraicas, desde la observación del comportamiento de sus raíces y las extensiones de cuerpos correspondientes y su relación con los automorfismos de cuerpos correspondientes.
Definición
Un cuerpo es un anillo de división conmutativo, es decir, un anillo conmutativo y unitario en el que todo elemento distinto de cero es invertible respecto del producto. Por tanto un cuerpo es un conjunto K en el que se han definido dos operaciones, + y ·, llamadas adición y multiplicación respectivamente, que cumplen las siguientes propiedades:
K es cerrado para la adición y la multiplicación
- Para todo a, b en K, a + b y a · b pertenecen a K (o más formalmente, + y · son operaciones matemáticas en K);
Asociatividad de la adición y la multiplicación
- Para toda a, b, c en K, a + (b + c) = (a + b) + c y a · (b · c) = (a · b) · c.
Conmutatividad de la adición y la multiplicación
- Para toda a, b en K, a + b = b + a y a · b = b · a.
Existencia de un elemento neutro para la adición y la multiplicación
- Existe un elemento 0 en K, tal que para todo a en K, a + 0 = a.
- Existe un elemento 1 en K, diferente de 0, tal que para todo a en K, a · 1 = a.
Existencia de elemento opuesto y de inversos:
- Para cada a en K, existe un elemento -a en K, tal que a + (- a) = 0.
- Para cada a ≠ 0 en K, existe un elemento a -1 en K, tal que a · a-1 = 1.
Distributividad de la multiplicación respecto de la adición
- Para toda a, b, c, en K, a · (b + c) = (a · b) + (a · c).
El requisito a ≠ 0 asegura que el conjunto que contiene solamente un cero no sea un cuerpo, y de paso elimina la posibilidad de que en el cuerpo existan divisores de cero distintos de 0, lo que lo convierte también en un dominio de integridad. Directamente de los axiomas, se puede demostrar que (K, +) y (K - { 0 }, ·) son grupos conmutativos y que por lo tanto (véase la teoría de grupos) el opuesto -a y el inverso a-1 son determinados únicamente por a. Además, el inverso de un producto es igual al producto de los inversos:
- (a·b)-1 = a-1 · b-1
con tal que a y b sean diferentes de cero. Otras reglas útiles incluyen
- -a = (-1) · a
y más generalmente
- - (a · b) = (-a) · b = a · (-b)
así como
- a · 0 = 0,
todas reglas familiares de la aritmética elemental.
Definiciones alternativas
Sintéticamente, Un anillo P se llama cuerpo, si consta no sólo del cero y en él es posible la división en todos los casos( salvo la división por cero), determinándose esta unívocamente, esto es, si para cualesquiera elementos m y n de P, de los cuales n es diferente de cero, existe en P un elemento q, y sólo uno, que cumple la igualdad nq= m. El elemento q se denomina cociente de los elementos m y n y se denota q = m/n.2
- Un cuerpo F es un dominio de integridad que contiene para cada elemento a ≠ 0 un «inverso» a-1 que verifica la igualdad:
- a-1·a = 1.3
Ejemplos de cuerpos
Racionales y algebraicos
Los números racionales es un cuerpo de números que incluye un subjconjunto isomorfo a los números enteros, que por abuso de notación también se designa como  . Todo número racional puede representarse por un conjunto de fracciones, pero el conjunto de los racionales no debe identificarse con el conjunto de las fracciones (ya que 1/2 y 2/4 son dos fracciones diferentes que representan el mismo número real. Para definir los racionales debe considerarse una relación de equivalencia sobre el conjunto de las fracciones:
. Todo número racional puede representarse por un conjunto de fracciones, pero el conjunto de los racionales no debe identificarse con el conjunto de las fracciones (ya que 1/2 y 2/4 son dos fracciones diferentes que representan el mismo número real. Para definir los racionales debe considerarse una relación de equivalencia sobre el conjunto de las fracciones:
 . Todo número racional puede representarse por un conjunto de fracciones, pero el conjunto de los racionales no debe identificarse con el conjunto de las fracciones (ya que 1/2 y 2/4 son dos fracciones diferentes que representan el mismo número real. Para definir los racionales debe considerarse una relación de equivalencia sobre el conjunto de las fracciones:
. Todo número racional puede representarse por un conjunto de fracciones, pero el conjunto de los racionales no debe identificarse con el conjunto de las fracciones (ya que 1/2 y 2/4 son dos fracciones diferentes que representan el mismo número real. Para definir los racionales debe considerarse una relación de equivalencia sobre el conjunto de las fracciones:
La relación de equivalencia entre dos fracciones a/b y c/d están relacionadas si ad = bc, es decir:
En esas condiciones el conjunto de los racionales es el conjunto de clases de equivalencia en que el conjunto de las fracciones queda dividido  .
.
 .
.
Los números racionales no forman un cuerpo algebraicamente cerrado, un importante teorema de la teoría de cuerpos demuestra la existencia de un cuerpo algebraicamente cerrado que contiene al primero (estrictamente un conjunto isomorofo). Dado que los racionales no son algebraicamente cerrados, existe y puede construirse su clausura algebraica 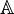 , este conjunto se denomina cuerpo de los números algebraicos, puede demostrarse que:
, este conjunto se denomina cuerpo de los números algebraicos, puede demostrarse que:
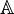 , este conjunto se denomina cuerpo de los números algebraicos, puede demostrarse que:
, este conjunto se denomina cuerpo de los números algebraicos, puede demostrarse que:
Los números complejos contienen tanto al cuerpo de números algebraicos como a los números reales. Sin embargo los reales no continen a los algabraicos ya que por ejemplo  . Además puede demostrarse que los números racionales y los números algebraicos son conjuntos numerables mientras que los reales y los complejos no lo son:
. Además puede demostrarse que los números racionales y los números algebraicos son conjuntos numerables mientras que los reales y los complejos no lo son:
 . Además puede demostrarse que los números racionales y los números algebraicos son conjuntos numerables mientras que los reales y los complejos no lo son:
. Además puede demostrarse que los números racionales y los números algebraicos son conjuntos numerables mientras que los reales y los complejos no lo son:Números reales, complejos y p-ádicos
Los números reales  con las operaciones usuales forman un cuerpo.
con las operaciones usuales forman un cuerpo.
 con las operaciones usuales forman un cuerpo.
con las operaciones usuales forman un cuerpo.
Los números hiperreales forman un cuerpo que contiene los reales, más los números infinitesimales e infinitos. Los números surreales forman un cuerpo que contiene los reales, a excepción del hecho de que son una clase propia, no un conjunto. El conjunto de todos los números surreales con el cumpleaños menor que un ciertocardinal inaccesible es un cuerpo.
Los números reales contienen varios subcuerpos interesantes: los números reales algebraicos, los números computables, y los números definibles.
Los números complejos  consisten en expresiones del tipo
consisten en expresiones del tipo
 consisten en expresiones del tipo
consisten en expresiones del tipo- a + bi
donde i es la unidad imaginaria, i.e., un número (no real) que satisface i2 = −1. Adición y multiplicación de los números reales son definidos de tal manera para que todos los axiomas del cuerpo se cumplen para C. Por ejemplo, la ley distributiva cumple
- (a + bi)·(c + di) = ac + bci + adi + bdi2, que es igual a ac−bd + (bc + ad)i.
Los números racionales se pueden ampliar a los cuerpos de números p-ádicos para cada número primo p.
Cuerpos finitos
El cuerpo más pequeño tiene solamente dos elementos: 0 y 1. Es denotado por  o
o  y puede a veces ser definido por las dos tablas
y puede a veces ser definido por las dos tablas
 o
o  y puede a veces ser definido por las dos tablas
y puede a veces ser definido por las dos tablas
Tiene aplicaciones importantes en informática, especialmente en álgebra de Boole, criptografía y teoría de la codificación.
Más generalmente, para un número primo  , el conjunto de los números enteros módulo
, el conjunto de los números enteros módulo  es un cuerpo finito con los
es un cuerpo finito con los  elementos: esto se escribe a menudo como
elementos: esto se escribe a menudo como  donde las operaciones son definidas realizando la operación en
donde las operaciones son definidas realizando la operación en  , dividiendo por
, dividiendo por  y tomando el resto, ver aritmética modular.
y tomando el resto, ver aritmética modular.
 , el conjunto de los números enteros módulo
, el conjunto de los números enteros módulo  es un cuerpo finito con los
es un cuerpo finito con los  elementos: esto se escribe a menudo como
elementos: esto se escribe a menudo como  donde las operaciones son definidas realizando la operación en
donde las operaciones son definidas realizando la operación en  , dividiendo por
, dividiendo por  y tomando el resto, ver aritmética modular.
y tomando el resto, ver aritmética modular.Cuerpos de funciones
Para un cuerpo dado K, el conjunto K(X) de funciones racionales en la variable X con coeficientes en K es un cuerpo; esto se define como el conjunto de cocientes depolinomios con coeficientes en K.
Si K es cuerpo, y p(X) es un polinomio irreducible en un anillo de polinomios F[X], entonces el cociente F[X]/<p(X)> es un cuerpo con un subcuerpo isomorfo a K. Por ejemplo, R[X]/(X2+1) es un cuerpo (de hecho, es isomorfo al cuerpo de los números complejos).
Cuando K es un cuerpo, el conjunto K[[X]] de series formales de Laurent sobre K es un cuerpo.
Si V es una variedad algebraica sobre K, entonces las funciones racionales V → K forman un cuerpo, el cuerpo de funciones V. Si S es una superficie de Riemann, entonces las funciones meromorfas de S → C forman un cuerpo.
Ultrafiltros
Si I es un conjunto de índices, U es un ultrafiltro sobre I, y Ki es un cuerpo para cada i en I, el ultraproducto de Ki (usando U) es un cuerpo.
Subcuerpos
Sean E y K dos cuerpos con E un subcuerpo de K (es decir, un subconjunto de K que contiene 0 y 1, cerrado bajo las operaciones + y * de K y con sus propias operaciones definidas por restricción). Sea x un elemento de K no en E. Entonces E(x) se define como el subcuerpo más pequeño de K que contiene a E y a x. Por ejemplo, Q(i) es el subcuerpo de los números complejos C que consisten en todos los números de la forma a+bi donde a y b son números racionales.
Algunos teoremas iniciales
- El conjunto de elementos diferentes de cero de un cuerpo K (denotado típicamente por K×) es un grupo abeliano bajo multiplicación. Cada subgrupo finito de K×es cíclico.
- La característica de cualquier cuerpo es cero o un número primo. (la característica se define como el número entero positivo más pequeño n tal que n·1 = 0, o cero si no existe tal n; aquí n·1 significa n sumandos 1 + 1 + 1 +... + 1.)
- Si
 es una potencia de un número primo, entonces existe (salvo isomorfismo) exactamente un cuerpo finito con
es una potencia de un número primo, entonces existe (salvo isomorfismo) exactamente un cuerpo finito con  elementos. Además, estos son los únicos cuerpos finitos posibles.
elementos. Además, estos son los únicos cuerpos finitos posibles.
- Como anillo, un cuerpo no tiene ningún ideal excepto {0} y sí mismo.
- Todo anillo de división finito es un cuerpo (teorema de Wedderburn).
- Para cada cuerpo K, existe (salvo isomorfismo) un cuerpo único G que contiene a K, es algebraico sobre K, y es algebraicamente cerrado. G se llama la clausuraalgebraica de K.
Construcciones de cuerpos
Subcuerpos e ideales
Si un subconjunto E de un cuerpo (K,+,·) junto con las operaciones ·, + restringido a E es en sí mismo un cuerpo, entonces se llama un subcuerpo de K. Tal subcuerpo tiene los mismos 0 y 1 que K.
Sea  un cuerpo, y
un cuerpo, y  . Se dice que
. Se dice que  es subcuerpo de
es subcuerpo de  o que
o que  es extensión de
es extensión de  si se cumple que
si se cumple que 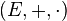 es un cuerpo cuando las operaciones
es un cuerpo cuando las operaciones  y
y  se restringen a
se restringen a  . En particular,
. En particular,  será entonces un subanillo de
será entonces un subanillo de  . Se tiene entonces que
. Se tiene entonces que  y
y  son subgruposrespectivos de los grupos abelianos
son subgruposrespectivos de los grupos abelianos  y
y  .
.
 un cuerpo, y
un cuerpo, y  . Se dice que
. Se dice que  es subcuerpo de
es subcuerpo de  o que
o que  es extensión de
es extensión de  si se cumple que
si se cumple que 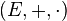 es un cuerpo cuando las operaciones
es un cuerpo cuando las operaciones  y
y  se restringen a
se restringen a  . En particular,
. En particular,  será entonces un subanillo de
será entonces un subanillo de  . Se tiene entonces que
. Se tiene entonces que  y
y  son subgruposrespectivos de los grupos abelianos
son subgruposrespectivos de los grupos abelianos  y
y  .
.
Como todo cuerpo es un anillo, podríamos preguntarnos por la forma que tengan sus ideales. Para empezar, como todo cuerpo es anillo conmutativo, todo ideal por la izquierda es ideal (bilátero) y todo ideal por la derecha es también ideal (bilátero). Así pues sólo hemos de estudiar los ideales del cuerpo.
Si  es ideal del cuerpo
es ideal del cuerpo  , entonces todo elemento no nulo
, entonces todo elemento no nulo 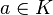 ha de tener inverso,
ha de tener inverso,  , luego
, luego  es una unidad de
es una unidad de  [esto es,
[esto es,  ], y se tendrá que
], y se tendrá que  , es decir,
, es decir,  . De esta manera, los únicos ideales de un cuerpo son el propio cuerpo y el ideal nulo.
. De esta manera, los únicos ideales de un cuerpo son el propio cuerpo y el ideal nulo.
 es ideal del cuerpo
es ideal del cuerpo  , entonces todo elemento no nulo
, entonces todo elemento no nulo 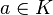 ha de tener inverso,
ha de tener inverso,  , luego
, luego  es una unidad de
es una unidad de  [esto es,
[esto es,  ], y se tendrá que
], y se tendrá que  , es decir,
, es decir,  . De esta manera, los únicos ideales de un cuerpo son el propio cuerpo y el ideal nulo.
. De esta manera, los únicos ideales de un cuerpo son el propio cuerpo y el ideal nulo.Cuerpo de fracciones
Dado un cuerpo  , el cuerpo polinómico
, el cuerpo polinómico  es el cuerpo de fracciones de polinomios en X con coeficientes en
es el cuerpo de fracciones de polinomios en X con coeficientes en  , es decir, sus elementos son funciones racionalescon coeficientes en
, es decir, sus elementos son funciones racionalescon coeficientes en  (técnicamente sobre las fracciones formadas por polinomios de
(técnicamente sobre las fracciones formadas por polinomios de ![\mathbb{K}[X]](https://upload.wikimedia.org/math/a/5/4/a54a58150f8fbfa21e4e47bea7551681.png) debe definirse una relación de equivalencia de tal manera que
debe definirse una relación de equivalencia de tal manera que
 , el cuerpo polinómico
, el cuerpo polinómico  es el cuerpo de fracciones de polinomios en X con coeficientes en
es el cuerpo de fracciones de polinomios en X con coeficientes en  , es decir, sus elementos son funciones racionalescon coeficientes en
, es decir, sus elementos son funciones racionalescon coeficientes en  (técnicamente sobre las fracciones formadas por polinomios de
(técnicamente sobre las fracciones formadas por polinomios de ![\mathbb{K}[X]](https://upload.wikimedia.org/math/a/5/4/a54a58150f8fbfa21e4e47bea7551681.png) debe definirse una relación de equivalencia de tal manera que
debe definirse una relación de equivalencia de tal manera que
donde:
Extensión de cuerpos
Véase también: Extensión de cuerpos
Una extensión algebraica de un cuerpo K es el cuerpo más pequeño que contiene a K y una raíz de un polinomio irreducible p(X) en K [X]. Alternativamente, es idéntico al anillo factor K [X]/(p(X)), donde (p(X)) es el ideal generado por p(X).
Cuerpo ordenado
Un cuerpo ordenado es un cuerpo en el que se puede definir una relación de orden que sea complatible con las operaciones de cuerpo, es decir:
 , para cualesquiera x, y y z.
, para cualesquiera x, y y z. , para cualesquiera x y z.
, para cualesquiera x y z. , para cualquier x
, para cualquier x
Los racionales 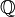 y los reales
y los reales  son cuerpos ordenados, en cambio en los complejos
son cuerpos ordenados, en cambio en los complejos  no es posible definir un orden compatible con las operaciones de grupo (si i > 0 se sigue que -1 > 0, si i < 0 se sigue que (-i)(-i) = -1 > 0).
no es posible definir un orden compatible con las operaciones de grupo (si i > 0 se sigue que -1 > 0, si i < 0 se sigue que (-i)(-i) = -1 > 0).
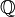 y los reales
y los reales  son cuerpos ordenados, en cambio en los complejos
son cuerpos ordenados, en cambio en los complejos  no es posible definir un orden compatible con las operaciones de grupo (si i > 0 se sigue que -1 > 0, si i < 0 se sigue que (-i)(-i) = -1 > 0).
no es posible definir un orden compatible con las operaciones de grupo (si i > 0 se sigue que -1 > 0, si i < 0 se sigue que (-i)(-i) = -1 > 0).Axiomas de cuerpo
Sea  un conjunto.Supongamos que en
un conjunto.Supongamos que en  definimos dos operaciones
definimos dos operaciones  y
y  que cumplen los siguientes axiomas; para cada
que cumplen los siguientes axiomas; para cada  ,
,  que pertenecen a
que pertenecen a  , se tiene que
, se tiene que  ,
,  son elementos de
son elementos de  . Consideremos éste como un axioma
. Consideremos éste como un axioma  , el cual garantiza que las operaciones estén bien definidas en
, el cual garantiza que las operaciones estén bien definidas en  .
.
1. Para todo  que pertenecen a
que pertenecen a  , se tiene:
, se tiene:  y
y  (
( y
y  son conmutativas)
son conmutativas)
2. Para todo  en
en  ,
,  y
y  (
( y
y  son asociativas)
son asociativas)
3. Para todo  en
en  ,
,  (
( es distributiva respecto a
es distributiva respecto a  )
)
4. Existen elementos  y
y  en
en  donde
donde  , tales que para todo
, tales que para todo  en
en  se tiene;
se tiene;  y
y  .
.  y
y  son llamados identidades, módulos o elementos neutros de la suma y el producto respectivamente (+ y son modulativas).
son llamados identidades, módulos o elementos neutros de la suma y el producto respectivamente (+ y son modulativas).
5. Para cada  en
en  existe
existe  en
en  , tal que
, tal que  , donde
, donde  es el mismo de la propiedad anterior.
es el mismo de la propiedad anterior.
6. Para cada  en
en  , con
, con  , existe
, existe  en
en  tal que
tal que 
Teorema
Si están en y , entonces
Teorema
Dados en , existe un único en , tal que
Definición
Al número  solución de la ecuación
solución de la ecuación  lo notaremos por
lo notaremos por  . En particular, si b = 0 (ver el axioma 5), entonces
. En particular, si b = 0 (ver el axioma 5), entonces  y así
y así , al cual llamaremos el inverso aditivo de
, al cual llamaremos el inverso aditivo de  , o el opuesto de
, o el opuesto de  .
.
Teorema
Para todo  y
y  en
en  ,
, 
Teorema
Para todo  en
en  ,
, 
Teorema
Para todo  en
en  ,
, 
Teorema
Para todo  ,
, 
 ,
, 
Teorema
Para todo  ,
, 
Teorema
Para todo  ,
, 
Teorema
Si  ,
,  y
y  , entonces
, entonces 
Teorema
Dados  ,
,  , existe un único
, existe un único  , tal que
, tal que 
Definición
Al número  solución de la ecuación
solución de la ecuación  ,
,  , lo notaremos por
, lo notaremos por  . En particular, si
. En particular, si  (ver el axioma 6), entonces
(ver el axioma 6), entonces , y así
, y así  , que notaremos por
, que notaremos por  y lo llamaremos el inverso multiplicativo de
y lo llamaremos el inverso multiplicativo de  , o el recíproco de
, o el recíproco de  .
.
Teorema
Si  y
y  , entonces
, entonces 
Teorema
Si  , entonces
, entonces  es invertible y
es invertible y 
Teorema
Sean  en
en  , Si
, Si  , entonces
, entonces  ó
ó 
Teorema
Dados  en
en  ,
,  ,
,
Teorema
Si  y
y  , entonces
, entonces 
Teorema
Si  , con
, con  y
y  , entonces
, entonces 
Teorema
Si  , con
, con  y
y  , entonces
, entonces 





![\mathbb{K}(X) = \left\{ \frac{p}{q} \Big|\ p,q \in \mathbb{K}[X], q\neq 0 \right\}/\mathcal{R}](https://upload.wikimedia.org/math/f/0/b/f0bd90c142889627eed648e54b8cf1ef.png)

No hay comentarios:
Publicar un comentario