jueves, 22 de octubre de 2015

Teorías matemáticas

Teoría de cuerpos

 extensión de cuerpo algebraica N/K es normal si N es el cuerpo de descomposición de una familia de polinomios en K[X].

Definición formal

Concretamente, una extensión es normal si verifica alguna de las siguientes condiciones equivalentes:
  • Para todo elemento  \alpha\in N, el polinomio irreducible de α en K sobre la variable x, denotado por \mathrm{Irr}(\alpha, K; x)\in K[x] descompone completamente en el cuerpo N (es decir, todas sus raíces pertenecen a N).
  • N es cuerpo de descomposición de alguna familia de polinomios T\subseteq K[x].
  • Dado un cuerpo \Omega algebraicamente cerrado, tal que N \subseteq\Omega, se cumple que cualquier K-inmersión \sigma : N \to \Omega es un automorfismo del cuerpo N respecto a K(\sigma\in \operatorname{Aut}_K(N)).









extensión separable de un cuerpo K es un cuerpo L que contiene a K y que puede ser generado adjuntando a Kun conjunto de elementos α, tales que son raíces de polinomios separables sobre K. En dicho caso, cualquier elemento β de L tiene asociado un polinomio mínimo que es separable sobre K.
La condición de separabilidad es importante en la teoría de Galois. Un cuerpo perfecto es aquel en que todas sus extensiones algebraicas son separables. Existe un criterio simple para ver si un cuerpo es perfecto: un cuerpo F es perfecto si y sólo si
  • F tiene característica 0, o
  • F tiene característica no nula p, y todo elemento de F es una raíz p-ésima de un elemento de F.
La segunda condición equivale a decir que el morfismo de Frobenius de F, x\mapsto x^p, es un automorfismo.
En particular, todo cuerpo de característica 0 y todo cuerpo finito es perfecto. Este hecho implica que la separabilidad puede ser supuesta en un gran número de contextos. Los efectos de la inseparabilidad (i.e. cuerpos de característica p infinitos) pueden ser vistos en el teorema del elemento primitivo, y en los productos tensoriales de cuerpos.
Dada una extensión finita de cuerpos L/K, existe un subcuerpo M de L que contiene K tal que L es una extensión separable de M. Cuando L = M la extensión L/K recibe el nombre de extensión inseparable pura.
Las extensiones inseparables puras aparecen en situaciones bastante naturales, por ejemplo en geometría algebraica en característicap. Si K es un cuerpo de característica p, y V una variedad algebraica sobre K de dimensión no nula, si consideramos el cuerpo de funciones K(V) y su subcuerpo K(V)p de potencias p-ésimas. Esta es siempre una extensión inseparable pura. Estas extensiones aparecen cuando uno estudia la multiplicación por p sobre una curva elíptica sobre un cuerpo de característica p.
En el contexto de cuerpos no perfectos, se introduce el concepto de clausura separable Ksep dentro de la clausura algebraica, la cual es la mayor extensión separable posible de K. Entonces la teoría de Galois es válida dentro de Ksep.









 extensión simple es una extensión de cuerpos L:K de manera que L está generado por un solo elemento, al cual se lo denomina elemento primitivo. Dicho de otro modo, un elemento primitivo de una extensión de cuerpos L/K es un elemento ζ de L tal que
L = K(ζ),
o en otras palabras, L está generado por ζ sobre K. Esto significa que todo elemento de L puede ser escrito como cociente de dos polinomios en ζ con coeficientes en K.
Si la extensión L/K es simple (es decir, si admite un elemento primitivo), entonces L puede ser una extensión finita de K (caso en el que ζ es un elemento algebraico deL sobre K), o en cambio L es isomorfo al cuerpo de funciones racionales sobre K en una indeterminada (en este caso ζ es un elemento trascendente de L sobre K).

Construcción

Sean L y K dos cuerpos de manera que L es extensión de K. Se define la extensión generada por \alpha sobre K como el conjunto
K(\alpha):= \{\frac{f(\alpha)}{g(\alpha)}: f,g \in K[x], g(\alpha) \neq 0\}.
Así K(\alpha) es exactamente el conjunto de los valores que se obtienen al evaluar en \alpha todas las funciones racionales definidas en K.

Propiedades

  • K(\alpha) es un subconjunto de L:
Todo elemento de K[x] está también en L[x], y como \alpha \in L, si f \in K[x] entonces f(\alpha) \in L. Si g \in K[x] entonces es g(\alpha) \in L, y si g(\alpha) \neq 0, existe g(\alpha)^{-1} \in L. Así pues, \frac{f(\alpha)}{g(\alpha)}:= f(\alpha) \cdot g(\alpha)^{-1} \in L y es K(\alpha) \subset L.
  • De hecho, K(\alpha) es subcuerpo de L.
Definimos las operaciones suma y producto en K(\alpha) como las restricciones a K(\alpha) de las operaciones del cuerpo de cocientes de L, i.e., si \frac{f(\alpha)}{g(\alpha)},\frac{p(\alpha)}{q(\alpha)} \in K(\alpha) , entonces:
\mathrm{i}) \quad \frac{f(\alpha)}{g(\alpha)} + \frac{p(\alpha)}{q(\alpha)}:= \frac{f(\alpha)q(\alpha)+p(\alpha)g(\alpha)}{g(\alpha)q(\alpha)}
\mathrm{ii}) \quad\frac{f(\alpha)}{g(\alpha)} \cdot \frac{p(\alpha)}{q(\alpha)} := \frac{f(\alpha)\cdot p(\alpha)}{g(\alpha)q(\alpha)}.
Por ser K[x] un anillo y L un cuerpo, es sencillo demostrar que la suma y el producto así definidos en K(\alpha) son operaciones internas en K(\alpha).
Como L es cuerpo, en particular es dominio de integridad, y por la Propiedad Universal del Cuerpo de Cocientes de un Dominio Íntegro, el cuerpo de cocientes de L es Q(L)=L (el menor cuerpo que contiene a L es el propio L). Así se demuestra que K(\alpha), con las operaciones así definidas, es subcuerpo de L.
  • K es un subconjunto de K(\alpha)
Para comprobar que K \subset K(\alpha), basta con tomar el cociente \frac{a(\alpha)}{1(\alpha)}=\frac{a}{1}=a para cada 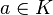a \in K (donde identificamos 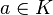a \in K con el polinomio constante a(x)=a \in K[x]). Además, como las operaciones en L son las extensiones de las operaciones en K, es inmediato que K es subcuerpo de K(\alpha).
Tomando el polinomio x \in K[x], entonces es \alpha = \frac{\alpha}{1}=\frac{x(\alpha)}{1(\alpha)}, luego \alpha \in K(\alpha).
Todo esto demuestra que K(\alpha) es una extensión de K y subcuerpo de L.
  • Finalmente, K(\alpha) es la menor extensión de K que contiene a \alpha:
Sea ahora una extensión E de K de forma que \alpha \in E. Como K(\alpha):= \{\frac{f(\alpha)}{g(\alpha)}: f,g \in K[x], g(\alpha) \neq 0\} y K \subset E, si f,g \in K[x], entonces f,g \in E[x], y como \alpha \in E, entonces f(\alpha), g(\alpha) \in E. Por último, como E es cuerpo, si g(\alpha) \neq 0, entonces existe g(\alpha)^{-1} \in E y \frac{f(\alpha)}{g(\alpha)} \in E, luego K(\alpha) \subset E.
Queda entonces demostrado que K(\alpha) es la menor extensión de K que contiene a \alpha. A este proceso se le denomina a veces adjunción de un elemento \alpha a un cuerpo K.

Observaciones

Una extensión simple K(\alpha):K puede ser algebraica o trascendente, dependiendo de si \alpha es un elemento algebraico o trascendente sobre K. Si \alpha es trascendente, entonces el grado [K(\alpha):K] de la extensión es infinito. Si \alpha es algebraico, entonces el grado [K(\alpha):K] de la extensión es finito. En concreto, [K(\alpha):K] = \deg(m_{\alpha}^k), siendo m_{\alpha}^K el polinomio mónico irreducible de \alpha sobre K. Se deduce que toda extensión simple que sea algebraica es de grado finito.
Recíprocamente, si la extensión L/K admite un elemento primitivo, entonces L puede ser una extensión finita de K, caso en el que ζ es un elemento algebraico de Lsobre K, o en cambio L es isomorfo al cuerpo de funciones racionales sobre K en una indeterminada, en este caso ζ es un elemento trascendente de L sobre K.

Teorema del elemento primitivo

El teorema del elemento primitivo responde a la pregunta de qué extensiones finitas de cuerpos tienen elementos primitivos, es decir, son simples. Por ejemplo, no es obvio que si se junta al cuerpo Q de números racionales las raíces de los siguientes polinomios
X2 − 2
y
X2 − 3,
llamadas α y β respectivamente, para obtener un cuerpo K = Q(α, β) de grado 4 sobre Q, donde K es Q(γ) para un elemento primitivo γ. De hecho, se puede ver que
γ = α + β
Las potencias de γi para 0 ≤ i ≤ 3 pueden ser expresadas como combinación lineal de 1, α, β y αβ a coeficientes enteros. Tomando dichas igualdades como un sistema lineal de ecuaciones, se puede resolver para α y β sobre Q(γ), la cual cosa implica que dicha elección de γ es en realidad un elemento primitivo en este ejemplo.

Enunciado

En general, el teorema del elemento primitivo se enuncia de la siguiente forma:
La extensión de cuerpo L/K es finita y tiene un elemento primitivo si y solo si hay un número finito de subextensiones de cuerpos F con K ⊆ F ⊆ L.

Consecuencias

Un importante corolario de dicho teorema afirma:
Toda extensión separable finita L/K tiene un elemento primitivo.
Dicho corolario es aplicable al ejemplo expuesto más arriba (y a muchos similares), ya que Q tiene característica 0 por lo que toda extensión finita sobre Q es separable.
Para extensiones inseparables (o no separables), se puede afirmar lo siguiente:
Si el grado de la extensión [L:K] es un número primo, entonces L/K tiene un elemento primitivo.
Si el grado de la extensión no es un número primo y la extensión no es separable, se pueden encontrar contraejemplos. Por ejemplo, si K es Fp(T,U), el cuerpo de las funciones racionales con dos indeterminadas T y U sobre el cuerpo finito con p elementos, y L se obtiene a partir de K adjuntando una raíz pesima de T, y de U, entonces no existe ningún elemento primitivo de L sobre K. De hecho se puede ver que para cualquier α en L, el elemento αp pertenece a K. Además tenemos que [L:K] = p2 pero no existen elementos de L con grado p2 sobre K, como un elemento primitivo debería tener.








Publicado por en

No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)