jueves, 22 de octubre de 2015

Teorías matemáticas

Teoría de cuerpos

extensión abeliana es una extensión de Galois cuyo grupo de Galois es abeliano. Cuando el grupo de Galois es un grupo cíclico, entonces tenemos una extensión cíclica.
Cualquier extensión finita de un cuerpo finito es una extensión cíclica. El desarrollo de la teoría de cuerpos de clases ha proporcionado información detallada sobre las extensiones abelianas de los cuerpos numéricos, cuerpos funcionales de curvas algebraicas sobre cuerpos finitos, y cuerpos locales.
Hay dos conceptos ligeramente diferentes de extensiones ciclotómicas: éstas pueden significar extensiones formadas mediante el adjuntado de raíces de la unidad, o subextensiones de tales extensiones. Los cuerpos ciclotómicos son ejemplos. Cualquier extensión ciclotómica (para otra definición) es abeliana.
Si un cuerpo K una n-ésima raíz primitiva de la unidad y la n-ésima raíz de un elemento de K es adjuntada, el resultado, llamadoextensión de Kummer es una extensión abeliana (si K tiene característica p se debe decir que p no divide a n, puesto que de otra manera, podría fallar, incluso en ser una extensión separable). Sin embargo, en general, el grupo de Galois de de las raíces n-ésimas de elementos operan conjuntamente sobre las raíces n-ésimas y sobre las raíces de la unidad, dando un grupo de Galois no abeliano comoproducto semidirecto. La teoría de Kummer proporciona una descripción completa del caso de extensión abeliano, y el teorema de Kronecker-Weber postula que si K es un cuerpo de números racionales, una extensión es abeliana si y sólo si es un subcuerpo de un cuerpo obtenido mediante el adjuntado de una raíz de la unidad.
Hay una importante analogía con el grupo fundamental en topología, el cual clasifica todos los espacios recubridores de un espacio: las coberturas abelianas son clasificadas mediante su abelianización, que se relaciona directamente con el primer grupo homológico.










extensión de cuerpo L/K se dice algebraica si cada elemento de L es algebraico sobre K, por ejemplo, si cada elemento de L es una raíz de algún polinomio distinto de cero con coeficientes en K. Las extensiones de cuerpos que no son algebraicas, i.e. que contienen elementos trascendentes, son llamadastranscendentes.
Por ejemplo, la extensión de cuerpos R/Q es trascendente, mientras que las extensiones de cuerpos C/R y Q(√2)/Q son algebraicas.

Propiedades

Si pensamos en L como un espacio vectorial sobre K, podemos considerar su dimensión. Esta dimensión es también llamada el grado de la extensión. Así, la extensiónL/K puede ser clasificada además como extensión finita o infinita de acuerdo con esta dimensión. Todas las extensiones trascendentes son de grado infinito. Esto además implica que todas las extensiones finitas son algebraicas.
Sin embargo lo contrario no es cierto: existen extensiones infinitas que son además algebraicas. Por ejemplo, el cuerpo de todos los números algebraicos es una extensión infinita algebraica de los números racionales.
Si a es algebraico sobre K, entonces K[a], el conjunto de todos los polinomios en a con coeficientes en K, es un cuerpo. Es una extensión de cuerpos algebraica de Kque tiene grado finito sobre K. En el caso especial de que K=Q, Q[a] es un ejemplo de cuerpo de números algebraicos.
Un cuerpo sin extensiones algebraicas propias es llamado algebraicamente cerrado. Un ejemplo es el de los números complejos. Cada cuerpo tiene una extensión algebraica que es algebraicamente cerrada (que se denomina su clausura algebraica), pero el probar esto en general, requiere cierta forma del axioma de elección.

Generalizaciones

La teoría de modelos generaliza la noción de extensión algebraica a teorías arbitrarias: una inmersión difeomorfa (incubamiento) de M en N se le llama extensión algebraica si para cada x en N existe una condición p con parámetros en M, tal que p(x) es cierta y el conjunto
\{y \in N | p(y) \}
es finito. Ocurre que aplicando esta definición a la teoría de cuerpos tenemos la definición usual de extensión algebraica. El grupo de Galois de N sobre M puede ser de nuevo definido como el grupo de automorfismos, y gran parte de la teoría de grupos de Galois puede ser desarrollada para el caso general.



Extensiones de cuerpos, polinomios minimales y elementos algebraicos y trascendentes.- ..................................................................:http://mate.dm.uba.ar/~mfarinat/materias/alg3/p2.pdf

EXTENSIONES ALGEBRAICAS .- ...........................................................:http://casanchi.com/mat/ext_algebraicas.pdf








extensiones de cuerpo son el problema fundamental de la Teoría de Cuerpos. Un cuerpo es un conjunto en el que las operaciones suma y producto están definidas y «funcionan bien». Cuando se construye una extensión de un cuerpo, se busca un conjunto más grande en el que las operaciones suma y producto sigan funcionando bien y además se puedan resolver las ecuaciones polinómicas.

Definición.

Sea (K, +, ·) un cuerpo. Un cuerpo L es una extensión de K si K es un subcuerpo de L, es decir si (L,+,·) es un cuerpo y (K,+,·) es un cuerpo con la restricción a K de las operaciones + y · en L. Si L es extensión sobre K se denota L:K o L/K.

Extensión sobre un cuerpo como espacio vectorial sobre el cuerpo

En efecto, La adición de K sirve también de adición en el espacio vectorial, y la multiplicación de un elemento de K por uno de L define el producto escalar del espacio vectorial:
Por definición de cuerpo, (L,+) es grupo abeliano, y podemos considerar el producto por escalares \cdot: K \times L \longrightarrow L como una restricción a K \times L del producto en \cdot: L \times L \longrightarrow. De esta forma es inmediato que se cumple que:
  • a \cdot (\alpha + \beta)= (a \cdot \alpha) + (a \cdot \beta),
  • (a+b) \cdot \alpha = (a \cdot \alpha) + (b \cdot \alpha),
  • (a \cdot (b \cdot \alpha))= (a \cdot b) \cdot \alpha,
  • 1 \cdot \alpha = \alpha,
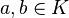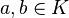cualesquiera que sean a,b \in K y \alpha,\beta \in L. Las dos primeras propiedades son debidas a la distributividad del producto respecto de la suma en L y a que K \subset L, la tercera se debe a que el producto es asociativo en L, y la cuarta se debe a que K es subcuerpo de L, por lo que el elemento unidad de L es el elemento unidad de K.

Extensión simple

El conjunto K(\alpha):= \{\frac{f(\alpha)}{g(\alpha)}: f,g \in K[x], g(\alpha) \neq 0\}. Este conjunto es un cuerpo, es extensión de K, es subcuerpo de L, y de hecho es la menor extensión de K que contiene a \alpha. Se le denomina extensión generada por α sobre K.

Extensiones algebraicas y trascendentes

Teorema de Kronecker.

Sea K un cuerpo y p \in K[x] un polinomio irreducible, entonces existe alguna extensión L:K de manera que p tiene alguna raíz en L.

Homomorfismo evaluación

La función \beta: K[x] \longrightarrow K(\alpha) que a cada polinomio p(x) \in K[x] le hace corresponder su evaluación en \alpha, i.e., \beta(p)=p(\alpha). Esta aplicación es de hecho unisomorfismo de anillos conmutativos y unitarios, y se denomina homomorfismo evaluación.

Extensión algebraica

Una extensión L:K se dice que es algebraica si todo elemento \alpha \in L es algebraico sobre K.

Elementos algebraicos

Supongamos que existe algún polinomio p \in K[x] que tiene a \alpha por raíz.
En esta situación (\ker(\beta) \neq \{0\}, o equivalentemente, existe algún p \in K[x] irreducible con \frac{K[x]}{(p)} \cong K(\alpha)) se dice que \alpha es algebraico sobre K.
Un elemento es entonces algebraico sobre un cuerpo si y sólo si es raíz de algún polinomio a coeficientes en dicho cuerpo.
Polinomio mónico irreducible
Si \alpha es un elemento algebraico sobre el cuerpo K de manera que \alpha \notin K, el polinomio p que genera al núcleo de la aplicación evaluación (i.e., \ker \beta = (p)) es irreducible. Dividiendo p por su coeficiente principal (aquél escalar que multiplica a la mayor potencia de la variable x) se obtiene un polinomio mónico (es decir, de manera que su coeficiente principal es la unidad), que se denota por m_{\alpha}^K y se denomina polinomio mónico irreducible de \alpha respecto de K.
Claramente, K(\alpha) \cong \frac{K[x]}{(m_{\alpha}^K)}.

Extensión trascendente

Una extensión L:K se dice que es trascendente si existe algún elemento \alpha \in L que sea trascendente sobre K.

Elementos trascendentes

Si el ker(\beta) = \{0\}, será \beta un monomorfismo. En ese caso, K(x) es isomorfo a K(\alpha).

Se dirá que el elemento \alpha es trascendente sobre K y que K(\alpha) es una extensión trascendente sobre K. Además, no existirá ningún polinomio con coeficientes en Kque tenga por raíz a \alpha (es decir, si p \in K[x], entonces p(\alpha) \neq 0).

Grado de una extensión

Como todo espacio vectorial tiene base, podemos calcular la dimensión de L como espacio vectorial sobre K, denotado por \operatorname{dim}_K(L). Se denomina grado de la extensión L:K a la dimensión de L como K-espacio vectorial: [L:K] = \operatorname{dim}_K(L).
Tomemos varios ejemplos:
K =  \mathbb{Q}  el cuerpo de los racionales y L =  \mathbb{R}  el cuerpo de los reales;  \mathbb{R}  visto como espacio vectorial sobre  \mathbb{Q} , es de dimensión infinita, es decir,  [\mathbb{R} : \mathbb{Q}] = \infty .
El resultado no sorprende si se considera los cardinales de ambos conjuntos: Si la dimensión de  \mathbb{R}  sobre  \mathbb{Q}  fuese finita,  \mathbb{R}  sería isomorfo a  \mathbb{Q}^{n} , n \in \mathbb{N}, lo que no es posible porque  |\mathbb{Q}^{n}| = |\mathbb{Q}| = |\mathbb{N}| < |\mathbb{R}|.
Si K =  \mathbb{Q} , el cuerpo de los racionales y L =  \mathbb{Q}(\sqrt{2}) , el menor cuerpo que contiene a la vez  \mathbb{Q}  y √2, claramente  \mathbb{Q}(\sqrt{2})  es una extension algebraica de  \mathbb{Q} , ya que  \sqrt{2} es raíz del polinomio  x^2 -2 .
Al mismo tiempo:
\mathbb{Q}(\sqrt{2}) \cong \mathbb{Q}[x]/(x^{2}-2)
ya que el ideal  (x^{2}-2)  es el nucleo del morfismo \beta: \mathbb{Q}[x] \longrightarrow \mathbb{Q}(\sqrt{2}), claramente este es un morfismo suprayectivo, se sigue del primer teorema de isomorfismo que son campos isomorfos.
Además  [\mathbb{Q}(\sqrt{2}) : \mathbb{Q}] = 2 , es decir, la dimensión de  \mathbb{Q}(\sqrt{2})  como espacio vectorial sobre  \mathbb{Q}  es 2, esto es así ya que 2 es el grado del polinomio mónico e irreducible que tiene a √2 como raíz:  x^2 - 2 .
En general:
[\mathbb{K}(\alpha) : \mathbb{K}] = n  si  n  es el grado del polinomio mónico e irreducible en  \mathbb{K}[x]  que tiene a  \alpha  como raíz, donde  \mathbb{K}  es un cuerpo y  \mathbb{K}[x]  son los polinomios con coeficientes en  \mathbb{K} .


Cuerpos y sus extensiones .- .................................................:https://www.uam.es/personal_pdi/ciencias/fchamizo/asignaturas/teogal1112/capitulo2.pdf


Extensiones de cuerpos. Extensiones algebraicas y finitas .- .....................................................:http://departamento.us.es/da/planantiguo/notas-ant/estructuras/t2.pdf 
Publicado por en

No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)