Unidades de ángulo
El estereorradián es la unidad derivada del SI que mide ángulos sólidos. Es el equivalente tridimensional del radián. Su símbolo es sr.
Definición
El estereorradián se define haciendo referencia a una esfera de radio r. Si el área de una porción de esta esfera es r2, un estereorradián es el ángulo sólido comprendido entre esta porción y el centro de la esfera.
Explicación de la definición
El ángulo sólido en estereorradianes, es:
Donde 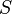 es la superficie cubierta por el objeto en una esfera imaginaria de radio
es la superficie cubierta por el objeto en una esfera imaginaria de radio  , cuyo centro coincide con el vértice del ángulo.
, cuyo centro coincide con el vértice del ángulo.
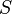 es la superficie cubierta por el objeto en una esfera imaginaria de radio
es la superficie cubierta por el objeto en una esfera imaginaria de radio  , cuyo centro coincide con el vértice del ángulo.
, cuyo centro coincide con el vértice del ángulo.
Por tanto, un estereorradián es el ángulo que cubre una superficie  a una distancia
a una distancia  del vértice.
del vértice.
 a una distancia
a una distancia  del vértice.
del vértice.- Analogía con el radián
En dos dimensiones, el ángulo en radianes, está relacionado con la longitud de arco, y es:
siendo s la longitud de arco, y r el radio del círculo.
Ángulo de un casquete esférico
Si el área  es igual a
es igual a  y está dada por el área de un casquete esférico (
y está dada por el área de un casquete esférico ( ) entonces se cumple que
) entonces se cumple que 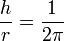 . Entonces el ángulo sólido descrito por el cono que corresponde al ángulo (plano, vea la figura) es igual a:
. Entonces el ángulo sólido descrito por el cono que corresponde al ángulo (plano, vea la figura) es igual a:
 es igual a
es igual a  y está dada por el área de un casquete esférico (
y está dada por el área de un casquete esférico ( ) entonces se cumple que
) entonces se cumple que 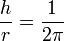 . Entonces el ángulo sólido descrito por el cono que corresponde al ángulo (plano, vea la figura) es igual a:
. Entonces el ángulo sólido descrito por el cono que corresponde al ángulo (plano, vea la figura) es igual a: .
.
Estereorradián
Los estereorradianes valen para medir ángulos "sólidos"Un estereorradián está relacionado con el área de la superficie de una esfera, de la misma manera en que unradián está relacionado con la longitud de una circunferencia:Un radián "marca" una longitud en una circunferencia igual a la del radio. Un estereorradián "marca" un área en una esfera igual a (radio)2. El nombre estereorradián se compone del griego stereos que significa "sólido" y radián. La abreviatura en el Sistema Internacional es "sr".Esfera y estereorradián
- El área de una esfera es 4πr2,
- El área de la superficie de un estereorradián es r2.
Así que una esfera mide 4π estereorradianes, más o menos 12.57 estereorradianes. De la misma manera un estereorradián es 1/12.57, más o menos 8% de una esfera.Y como estás midiendo ángulos, no importa el tamaño de la esfera, siempre mide 4π estereorradianes.Ejemplo: una esfera de radio 1 (llamada una "esfera unidad"):- tiene una superficie de 4π,
- y un estereorradián "cubriría" un área de 1.
Intensidad radiante
La intensidad radiante (con cuánta intensidad brilla algo) se puede medir en vatios por estereorradián (W/sr).Ejemplo: Quieres medir la luz que sale de una esfera brillante. Tu sensor mide 50mm × 50mm y si lo pones a 2 m marca 0.1 vatios. ¿Cuál es la intensidad radiante en W/sr?Respuesta: A 2 m, un estereorradián corresponde a 2×2 = 4 m2 de la esfera.Y como el sensor es bastante pequeño, su superficie plana es más o menos el área de la esfera que ocupa. Así que son 0.05×0.05=0.0025m2.Entonces, un estereorradián recibiría 0.1 W × (4m2/0.0025m2) = 160 W/sr.En grados
Igual que se puede convertir de radianes a grados también puedes convertir estereorradianes en "grados cuadrados":Un radián son 180/π grados, aproximadamente 57.296°.un estereorradián son entonces (180/π)2 grados cuadrados, aproximadamente 3282.8 grados cuadrados.- grado centesimal o gon —también llamado gradián (plural: gradianes), pero no gonio1 — es una unidad de medida de ángulos planos, alternativa al grado sexagesimal y, como este, no perteneciente al Sistema Internacional de Unidades, cuyo valor se define como el ángulo central subtendido por un arco cuya longitud es igual a 1/400 de la circunferencia. La circunferencia se divide, por tanto, en 400 gon y un ángulo recto en cien gon, lo que permite determinar que un grado centesimal equivale a nueve décimas partes del grado sexagesimal.2 Su símbolo es una "g" minúscula en superíndice colocada tras la cifra (por ejemplo, 12,4574g).La denominación de gon suele restringirse a los ámbitos especializados de la topografía y la ingeniería civil, donde es muy utilizada esta unidad de medida para definir el valor de los ángulos. La denominación de gradián se emplea en las calculadoras, en las que suele representarse con la abreviatura grad.Sus divisores son:
- 1 grado centesimal = 100 minutos centesimales (100m o 100c)
- 1 minuto centesimal = 100 segundos centesimales (100s o 100cc)
Existía una denominación anterior de esta unidad como grado centígrado. Para evitar confusiones, en 1948 la unidad homónima de temperatura del mismo nombre pasó a denominarse oficialmente grado Celsius, aunque popularmente el grado celsius se siga denominando centígrado.3 Esto es parcialmente incorrecto, ya que la escala Kelvin también es centígrada (es una escala que toma de referencia 100 partes iguales, en este caso, punto de congelación y ebullición del agua destilada) y el término sería ambiguo. Relación con el tamaño de la Tierra
Atendiendo a la definición de metro utilizada en 1889, un kilómetro debería corresponder a la longitud de un arco de meridiano cuya amplitud es un minuto centesimal; aunque mediciones posteriores más precisas del tamaño de la Tierra mostraron que existen diferencias.Equivalencias
El grado centesimal surge de la división del plano cartesiano en cuatrocientos ángulos iguales, con vértice común. Cada cuadrante posee una amplitud 100 grados centesimales, y la suma de los cuatro cuadrantes mide 400 grados centesimales.- Equivalencia entre grados sexagesimales y centesimales
- 0° = 0g
- 90° = 100g
- 180° = 200g
- 270° = 300g
- 360° = 400g
- Ejemplo
Los siguientes valores angulares son equivalentes:- 23° 47' 35" grados sexagesimales
- 23,7931º grados sexagesimales con fracción decimal
- 26g 43c 67cc gons con minutos y segundos centesimales
- 26,4367g gons o grados centesimales
Los minutos y segundos de gon se corresponden con la fracción decimal de gon, cosa que no ocurre con los grados sexagesimales. No deben confundirse los grados centesimales con el uso de fracciones decimales para expresar ángulos en grados sexagesimales.Conversión de ángulos comunes
Unidades Valores Revolución 0 






Grados sexagesimales 0° 30° 45° 60° 90° 180° 270° 360° Radianes 0 




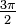

Grados centesimales 0g 
50g 
100g 200g 300g 400g - convertidor de los grados centesimal .- ..............................................:http://www.convertworld.com/es/angulo/Grado+centesimal.html
- ÁNGULOS
DEFINICIONES:
Ángulo: del Latín 'angulus', rincón.
Intuitivamente, desde un punto de vista estático, la idea de ángulo traduce la mayor o menor abertura de dos semirrectas a y b, llamadas lados, que parten de un mismo punto O, llamadovértice.
Dos ángulos son iguales si al superponer sus vértices coinciden sus lados respectivos (sin importar el orden).
Se puede establecer una correspondencia biyectiva entre los ángulos de un plano y los sectores, o con los arcos, de una circunferencia de radio unidad:
Ciertos ángulos, como los de la figura adjunta, reciben nombres especiales:
Para medir un ángulo se utiliza el arco que determinan los lados en la circunferencia cuyo centro es el vértice.
Si la unidad de medida del arco es el radio de la circunferencia, se dice que el ángulo se mide en radianes; así que un ángulo completo mide 2p radianes, ya que la longitud de la circunferencia es 2p r, siendo r su radio.
Si la circunferencia se divide en 360 partes iguales, cada parte se denomina un grado sexagesimal.
Si la circunferencia se divide en 400 partes iguales, cada una se llama un grado centesimal.
Los ángulos menores que un recto, se llaman agudos y los mayores que un recto se denominan obtusos.
Algunos ejemplos de medidas de ángulos:
Para sumar dos ángulos, se superponen sus vértices y el segundo ángulo se coloca a continuación del primero, de modo que tengan un lado común. Si la suma pasa de un ángulo completo, entonces se elimina este y nos quedamos sólo con la parte restante.
Los ángulos tal como acabamos de definirlos (que suelen llamarse sectores ángulares) pueden caracterizarse por un par de semirrectas, sin importar el orden.
Si se considera, dinámicamente, que un ángulo representa una rotación, entonces los ángulos tienen signo, según se considere que la semirrecta a gira hacia la semirrecta b, o al contrario:
Estos ángulos orientados se pueden representar por un par ordenado de semirrectas: a^b. El ángulo a^a representa el ángulo nulo.
Ahora, para sumar dos ángulos hay que colocar la primera semirrecta del segundo ángulo sobre la segunda del primero). Se cumple la relación de Chasles:
a^b + b^c =a^c
y, por tanto:
a^b=-b^a
COMENTARIOS:
La Naturaleza y el Arte parecen preferir ángulos de 72º, 120º, 90º y 60º. El primero suelen preferirlo muchas flores; el segundo es muchas veces el resultado del cuarteamiento de superficies, …
Nota: Además de las fotos que aquí se presentan, pueden analizarse las del apartado de polígonos
RELACIONES:
Ángulos opuestos por el vértice:
Dos rectas que se cortan, determinan ángulos iguales.
Ángulos alternos internos:
Dos rectas paralelas cortadas por otra recta determinan ángulos iguales,
Ángulos en un polígono:
Ángulos en una circunferencia:
Ángulo entre dos curvas que se cortan:
Es el ángulo que forman las rectas tangentes, si existen, a las curvas en el punto de corte P
Ángulo diedro entre dos planos que se cortan:
Es el ángulo que forman una semirrecta contenida en uno de los planos, perpendicular a la recta intersección por un punto P, y otra semirrecta, contenida en el otro plano, perpendicular a la recta intersección por el mismo punto P.
Por ejemplo, el angulo diedro que forman entre si cada dos caras consecutivas de un cubo es 90º; el ángulo diedro de las caras de un tetraedro es
Ángulo de una recta y un plano:
Es el ángulo que forma la recta con la recta intersección del plano que pasa por aquella y es perpendicular al plano.
Ángulo de dos superficies en un punto de intersección:
Es el ángulo que forman sus planos tangentes en el punto de intersección, si existen.
Ángulo sólido:
Es el espacio comprendido dentro de una superficie cónica (o piramidal).
Para medir un ángulo sólido, se traza una esfera de radio r y centro el vértice O del ángulo. Si S es el área de la superficie esférica interceptada por el ángulo sólido sobre la esfera, el cociente S/r2 es el valor del ángulo sólido en estereorradianes. Como la superficie de la esfera es 4p r2, la medida de un ángulo sólido completo es 4p estereorradianes.
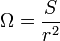




No hay comentarios:
Publicar un comentario