Análisis de Nodos
El análisis de nodos es completamente general y siempre se puede aplicar a cualquier red eléctrica.
Procedimiento paso a paso
Paso 1: referenciar cada elemento
Paso 2: localizar y enumerar los nodos
Paso 3: elegir un nodo de referencia
Paso 4: definir un voltaje entre cada nodo y el nodo de referencia.
Paso 5: obtener ecuaciones. Aplicar LCK a cada nodo
Paso 6: resolver el sistema de ecuaciones
Ejemplo 1 análisis de nodos
Dos fuentes de corriente
PASO 1: REFERENCIAR CADA ELEMENTO
Para facilitar la comprensión del circuito se referencia cada elemento del circuito, usando los subíndices S para las fuentes (sources)
PASO 2: ENUMERAR LOS NODOS Y ELEGIR UN NODO DE REFERENCIA
En un circuito con N nodos deberán haber N-1 voltajes desconocidos y N-1 ecuaciones. Se elige como nodo de referencia aquel al cual están conectadas el mayor número de ramas.
El nodo de referencia tiene cuatro ramas conectadas.
PASO 3: DEFINIR UN VOLTAJE ENTRE CADA NODO Y EL NODO DE REFERENCIA.
Supondremos que el nodo de referencia es de CERO VOLTIOS.
Debe haber N-1 voltajes de nodo desconocidos. Como hay tres nodos, hay 2 voltajes desconocidos, V1 y V2 y dos ecuaciones.
Los voltajes se definen entre pares de nodos. Se sobreentiende que el voltaje colocado en cada uno de los nodos es el voltaje de ese nodo respecto al nodo de referencia. Si se elige un nodo de referencia diferente, los voltajes serán diferentes.
Esta es la única situación en la cual se usará el voltaje en el nodo sin los signos más-menos, exceptuando que se trate de una batería.
PASO 4: OBTNENER ECUACIONES. APLICAR LCK A CADA NODO
Para obtener un conjunto de ecuaciones se aplica LCK a cada nodo, excepto al de referencia, Al nodo de referencia nunca se aplica LCK.
Para evitar equivocaciones al aplicar LCK se recorre cada nodo en forma circular de izquierda a derecha, comenzando por la cola y terminando en la punta de flecha. Debe haber N-1 ecuaciones. Es decir, en este caso debe haber dos ecuaciones.
LCK en nodo N1
Se puede emplear suma de corrientes que entran igual a cero, o suma de corrientes que salen igual a cero, o suma de corrientes que entran igual a suma de corrientes que salen. Se debe procurar no trazar las flechas de corriente en cada nodo, sino visualizarlas mentalmente. En este caso hemos considerado que todas las corrientes SALEN de cada nodo.
Aplicar la Ley de Ohm
Multiplicamos ambos lados por 10:
LCK en nodo N2
Multiplicamos ambos lados por 5:
Observe que:
Además, para la corriente I2, como V1 aparece primero la flecha va desde V1 hacia V2 , y para I4 la flecha va desde V2 hacia V1.
De nuevo, no es necesario colocar las fechas de corriente. Se ha hecho para dar claridad.
PASO 5: RESOLVER EL SISTEMA DE ECUACIONES
Se resuelve el sistema de ecuaciones, para obtener los voltajes de nodo, usando determinantes, o cualquier otro método de solución de ecuaciones como reducción, sustitución, igualación o eliminación gausiana.
Multiplicamos la Ec 2 por 7:
Sumamos Ec 1 y Ec 3:
Una vez obtenidos los voltajes es fácil obtener las corrientes aplicando la Ley de Ohm y LCK.
Ejemplo 2 análisis de nodos
Tres fuentes de corriente (matriz de conductancias simétrica)
PASO 1: REFERENCIAR CADA ELEMENTO
Para facilitar la comprensión del circuito se referencia cada elemento del circuito, usando los subíndices S para las fuentes (sources)
PASO 2: ENUMERAR LOS NODOS Y ELEGIR UN NODO DE REFERENCIA
En este caso hay 4 nodos. Se elige como nodo de referencia aquel al cual están conectadas el mayor número de ramas, es decir, el nodo 4 que tiene cuatro ramas. También se pudo haber escogido el nodo 2 como referencia.
PASO 3: DEFINIR VOLTAJES ENTRE CADA NODO Y EL NODO DE REFERENCIA.
Debe haber N-1 voltajes de nodo desconocidos. Como hay cuatro nodos, hay 3 voltajes desconocidos, V1, V2 y V3.
PASO 4: OBTENER ECUACIONES. APLICAR LCK A CADA NODO
Para obtener un conjunto de ecuaciones se aplica LCK a cada nodo, excepto al de referencia, Debe haber N-1 ecuaciones, es decir, debe haber 3 ecuaciones.
Para evitar equivocaciones al aplicar LCK se recorre cada nodo en forma circular de izquierda a derecha, comenzando por la cola y terminando en la punta de flecha.
LCK en nodo N1
Tenga cuidado al aplicar la Ley de Ohm, pues se trata de conductancias.
LCK en nodo N2
LCK en nodo N3
PASO 5: RESOLVER EL SISTEMA DE ECUACIONES
Se resuelve el sistema de ecuaciones, para obtener los voltajes de nodo, usando determinantes, o cualquier otro método de solución de ecuaciones como reducción, sustitución, igualación o eliminación gausiana.
Forma matricial del sistema:
G es la matriz de conductancias simétrica, aunque no se corresponde con los valores de las conductancias en el circuito. Sirve como forma de verificación si se ha cometido un error al escribir las ecuaciones en un circuito solo con fuentes independientes de corriente.
Se hace fácil ahora determinar las corrientes en cada nodo, aplicando la fórmula: I = GV. Se han cambiado las direcciones de las flechas cuya corriente es negativa para facilitar la verificación de corrientes en cada nodo.
Ejemplo 3 análisis de nodos
Una fuente de voltaje (supernodos)
PASO 1: REFERENCIAR CADA ELEMENTO
Para facilitar la comprensión del circuito se referencia cada elemento del circuito, usando los subíndices S para las fuentes (sources)
PASO 2: ENUMERAR LOS NODOS Y ELEGIR UN NODO DE REFERENCIA
En este caso hay 4 nodos. Se elige como nodo de referencia aquel al cual están conectadas el mayor número de ramas, es decir, el nodo 4 que tiene cuatro ramas. También se pudo haber escogido el nodo 2 como referencia.
PASO 3: DEFINIR VOLTAJES ENTRE CADA NODO Y EL NODO DE REFERENCIA.
Los voltajes se definen entre pares de nodos. Como hay cuatro nodos, deberá haber tres voltajes desconocidos y tres ecuaciones.
PASO 4: ESTABLECER SUPERNODO SOBRE FUENTES DE VOLTAJE SI LAS HAY
Cuando hay presente una fuente de voltaje, se establece un supernodo alrededor de esa fuente.
En este caso establecemos un supernodo en torno a la fuente de 22V
PASO 5: OBTENER ECUACIONES. APLICAR LCK A CADA NODO Y SUPERNODO
Se aplica LCK a cada nodo y supernodo, excepto al de referencia, para obtener un conjunto de ecuaciones.
Debe haber N-1 ecuaciones. Es decir, debe haber 3 ecuaciones. La inclusión de una fuente de voltaje reduce en uno el número de nodos a los que se aplica LCK.
Para evitar equivocaciones al aplicar LCK se recorre cada nodo en forma circular de izquierda a derecha. Se debe evitar considerar una corriente en la fuente de voltaje.
LCK en nodo N1
LCK en supernodo N2-N3
Ecuación de la fuente de voltaje (supernodo N2-N3)
Como apenas hay dos ecuaciones, la otra ecuación se obtiene de la fuente de voltaje ubicada en el supernodo.
PASO 6: RESOLVER EL SISTEMA DE ECUACIONES
Se resuelve el sistema de ecuaciones, para obtener los voltajes de nodo, usando determinantes, o cualquier otro método de solución de ecuaciones como reducción, sustitución, igualación o eliminación gausiana.
Se organizan para resolver por determinantes:
G ya no es una matriz de conductancias propiamente dicha, ya que la ecuación 3 no tiene nada que ver con conductancias.
He resuelto este sistema con el programa Microsoft Mathematics 4.0
Por último, se calculan las corrientes y se verifican en cada nodo.
Ejemplo 4 análisis de nodos
Cuatro tipos de fuentes
PASO 1: REFERENCIAR CADA ELEMENTO
Para facilitar la comprensión del circuito se referencia cada elemento del circuito, usando los subíndices S para las fuentes (sources)
PASO 2: ENUMERAR LOS NODOS Y ELEGIR UN NODO DE REFERENCIA
En este caso hay cinco nodos. Se elige como nodo de referencia aquel al cual están conectadas el mayor número de ramas, es decir, el nodo 5 que tiene cuatro ramas.
PASO 3: DEFINIR VOLTAJES ENTRE CADA NODO Y EL NODO DE REFERENCIA.
Los voltajes se definen entre pares de nodos. Debe haber N-1 voltajes de nodo desconocidos, es decir, 4 voltajes. Se sobreentiende que el voltaje colocado en cada uno de los nodos es el voltaje de ese nodo respecto al nodo de referencia, que se considera de cero voltios.
Esta es la única situación en la cual se usará el voltaje en el nodo sin los signos más-menos, exceptuando que se trate de una batería.
PASO 4: ESTABLECER SUPERNODOS SOBRE FUENTES DE VOLTAJE SI LAS HAY
Cuando hay presente una fuente de voltaje, se establece un supernodo alrededor de esa fuente. En este caso establecemos un supernodo en torno a la fuente Vs1 y otro en torno a la fuente Vs2.
PASO 5: OBTENER ECUACIONES. APLICAR LCK A CADA NODO
Se aplica LCK a cada nodo y supernodo, excepto al de referencia, para obtener un conjunto de ecuaciones.
Debe haber N-1 ecuaciones. Es decir, debe haber 4 ecuaciones.
Para evitar equivocaciones al aplicar LCK se recorre cada nodo en forma circular de izquierda a derecha, comenzando por la cola y terminando por la punta de flecha.
Ecuación de la fuente de voltaje (supernodo N1-REF)
Observe que no se puede aplicar LCK en este supernodo porque es el de referencia, pero si podemos establecer el voltaje de la fuente.
LCK en nodo N2:
Multiplicamos ambos lados por 2:
Obtenemos Vx de la variable de control:
LCK en supernodo N3-N4
Obtenemos Vx y Vy de las variables de control:
Multiplicamos ambos lados por 10:
Ecuación de la fuente de voltaje (supernodo N3-N4)
Multiplicamos por 5 ambos lados:
PASO 6: RESOLVER EL SISTEMA DE ECUACIONES
Se resuelve el sistema de ecuaciones, para obtener los voltajes de nodo, usando determinantes, o cualquier otro método de solución de ecuaciones como reducción, sustitución, igualación o eliminación gausiana.
Sustituimos V1 en todas las ecuaciones:
Por último calculamos las corrientes y verificamos la suma en cada nodo.
Ejemplo 5 análisis de nodos
Una fuente de tensión dependiente
PASO 1: REFERENCIAR CADA ELEMENTO
PASO 2: ENUMERAR LOS NODOS Y ELEGIR UN NODO DE REFERENCIA
Elegimos como nodo de referencia el nodo tierra o GROUND del amplificador.
PASO 3: DEFINIR VOLTAJES ENTRE CADA NODO Y EL NODO DE REFERENCIA.
PASO 4: OBTENER ECUACIONES. APLICAR LCK A CADA NODO
Hay 4 nodos, lo que debe dar tres voltajes desconocidos, y tres ecuaciones de nodo.
El objetivo será definir el voltaje de salida Vo en términos del voltaje de entrada Vs.
LCK en nodo Vo
Ecuación de la fuente de voltaje (supernodo V2-ref)
Ecuación de la fuente de voltaje (supernodo V3-ref)
PASO 5: RESOLVER EL SISTEMA DE ECUACIONES
Sustituimos Ec 2 y Ec 3 en Ec 1
Separamos en Vo y Vs:
Factor común Vo y Vs:
Sustituimos los valores de Ri, Ro y RL
Análisis de nodos en circuitos resistivos
El método de análisis de nodos es muy utilizado pararesolver circuitos resistivos lineales (este método, un poco más ampliado, se aplica a también a circuitosresistivos – reactivos)
Resolver en este caso significa obtener los valores que tienen las tensiones en todas las resistencias que haya en el circuito. Conociendo estos valores se pueden obtener otros datos como: corrientes, potencias, etc., en todos los elementos del circuito. El análisis de nodos se basa en la ley de corrientes de Kirchoff:
La suma algebraica de las corrientes que salen y entran de un nodo es igual a cero.
Donde un nodo se define como el lugar en el circuito donde se unen de dos o más ramas.
Pasos a seguir en el análisis de nodos son:
- Convertir todas las fuentes de tensión en fuentes de corriente (ver Teorema de Norton)
- Escoger un nodo para que sea el nodo de referencia (usualmente se escoge tierra).
- Etiquetar todos los otros nodos con V1, V2, V3, V4, etc.
- Armar una tabla para formar las ecuaciones de nodos. Hay 3 columnas y el número de filas depende del número de nodos (no se cuenta el nodo de referencia)
- El término de la columna A es la suma de las conductancias que se conectan con en nodo N multiplicado por VN
- Los términos de la columna son las conductancias que se conectan al nodo N y a otro nodo X por VX (El nodo de referencia no se incluye como nodo X). Pueden haber varios términos en la columna B. Cada uno de ellos se resta del término de la columna A.
- El término de la columna C, al lado derecho del signo de igual, es la suma algebraica de todas las fuentes de corriente conectadas al nodo N. La fuente es considerada positiva si suministra corriente hacia el nodo (al nodo) y negativa si la corriente sale del nodo
- Una vez elaborada la tabla, se resuelve el sistema de ecuaciones para cada VN. Se puede hacer por el método de sustitución o por el método de determinante. Al final si un valor de V tiene un valor negativo significa que la tensión original supuesto para el era el opuesto
Ejemplo de análisis de nodos:
Obtener los valores de las tensiones V1 y V2 en al gráfico siguiente:
Figura # 1
Primero se transforman todas las fuentes de tensión en fuentes de corriente (Teorema de Norton) y se obtiene el primer circuito (Figura # 2). Después se calculan las resistencias equivalentes de las resistencias en paralelo(2 y 4 ohmios en V1 ) y (2 y 4 ohmios en V2). (Figura # 3).
Figura # 2
Figura # 3
En el análisis de nodos, es más cómodo utilizar conductancias en vez de resistencias. Se transforma cada una de ellas en su valor de conductancia correspondiente y se obtiene el circuito que sigue:
Se escoge el nodo inferior (unión de todas las resistencias menos la de 5 ohmios) como nodo de referencia y se etiquetan los otros nodos V1 y V2, como se ve en al figura. Se implementa la tabla de dos filas (2 ecuaciones) pues hay dos nodos sin tomar en cuenta el nodo de referencia.
Con la tabla generada se procede a la solución de las variables V1 y V2, ya sea por el método de sustitución o con ayuda de determinantes. Los resultados son: V1 = 9.15 voltios, V2 = – 6.5 voltios.
análisis de nodos, o método de tensiones nodales es un método para determinar la tensión (diferencia de potencial) de uno o más nodos.
Cuando se analiza un circuito por las leyes de Kirchhoff, se podrían usar análisis de nodos (tensiones nodales) por la ley de corrientes de Kirchhoff (LCK) o análisis de malla (corrientes de malla) usando la ley de tensiones de Kirchhoff (LVK). En el análisis de nodos se escribe una ecuación para cada nodo, con condición que la suma de esas corrientes sea igual a cero en cualquier instante, por lo que una carga  nunca puede acumularse en un nodo. Estas corrientes se escriben en términos de las tensiones de cada nodo del circuito. Así, en cada relación se debe dar la corriente en función de la tensión que es nuestra incógnita, por laconductancia. Por ejemplo, para un resistor, Irama = Vrama * G, donde G es la Conductancia del resistor.
nunca puede acumularse en un nodo. Estas corrientes se escriben en términos de las tensiones de cada nodo del circuito. Así, en cada relación se debe dar la corriente en función de la tensión que es nuestra incógnita, por laconductancia. Por ejemplo, para un resistor, Irama = Vrama * G, donde G es la Conductancia del resistor.
 nunca puede acumularse en un nodo. Estas corrientes se escriben en términos de las tensiones de cada nodo del circuito. Así, en cada relación se debe dar la corriente en función de la tensión que es nuestra incógnita, por laconductancia. Por ejemplo, para un resistor, Irama = Vrama * G, donde G es la Conductancia del resistor.
nunca puede acumularse en un nodo. Estas corrientes se escriben en términos de las tensiones de cada nodo del circuito. Así, en cada relación se debe dar la corriente en función de la tensión que es nuestra incógnita, por laconductancia. Por ejemplo, para un resistor, Irama = Vrama * G, donde G es la Conductancia del resistor.
El análisis de nodos es posible cuando todos los nodos tienen conductancia. Este método produce un sistema de ecuaciones que puede resolverse a mano si es pequeño, o también puede resolverse rápidamente usando álgebra lineal en un computador. Por el hecho de que forme ecuaciones muy sencillas, este método es una base para muchos programas de simulación de circuitos (por ejemplo, SPICE). Cuando los elementos del circuito no tienen conductancia, se puede usar una extensión más general del análisis de nodos: el análisis de nodos modificado.
Los ejemplos simples de análisis de nodos se enfocan en elementos lineales. Las redes no lineales (que son más complejas) también se pueden resolver por el análisis de nodos al usar el método de Newton para convertir el problema no lineal en una secuencia de problemas lineales.
Procedimiento
- Localice los segmentos de cable conectados al circuito. Estos serán los nodos que se usarán para el método.
- Seleccione un nodo de referencia (polo a tierra). Se puede elegir cualquier nodo ya que esto no afecta para nada los cálculos; pero elegir el nodo con más conexiones podría simplificar el análisis.
- Identifique los nodos que están conectados a fuentes de voltaje que tengan una terminal en el nodo de referencia. En estos nodos la fuente define la tensión del nodo. Si la fuente es independiente, la tensión del nodo es conocida. En estos nodos no se aplica la LCK.
- Asigne una variable para los nodos que tengan tensiones desconocidas. Si la tensión del nodo ya se conoce, no es necesario asignarle una variable. (Véase Figura 2)
- Para cada uno de los nodos, se plantean las ecuaciones de acuerdo con las Leyes de Kirchhoff. Básicamente, sume todas las corrientes que pasan por el nodo e igualelas a 0. Si el número de nodos es
 , el número de ecuaciones será por lo menos
, el número de ecuaciones será por lo menos  porque siempre se escoge un nodo de referencia el cual no se le elabora ecuación.
porque siempre se escoge un nodo de referencia el cual no se le elabora ecuación. - Si hay fuentes de tensión entre dos tensiones desconocidas, una esos dos nodos como un supernodo, haciendo el sumatorio de todas las corrientes que entran y salen en ese supernodo. Las tensiones de los dos nodos simples en el supernodo están relacionadas por la fuente de tensión intercalada.
- Resuelva el sistema de ecuaciones simultáneas para cada tensión desconocida.
Ejemplos
Ejemplo 1: Caso básico
La única tensión desconocida en este circuito es V1. Hay tres conexiones en este nodo y por esta razón, 3 corrientes a considerar. Ahora se analiza todas las corrientes que pasan por el nodo, así:

Con ley de corrientes de Kirchhoff (LCK), tenemos:

Se resuelve con respecto a V1:

Finalmente, la tensión desconocida se resuelve sustituyendo valores numéricos para cada variable. Después de haber obtenido estas ecuaciones y conocer cada tensión, es fácil calcular cualquier corriente desconocida.
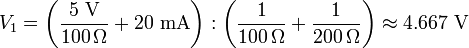
Ejemplo 2
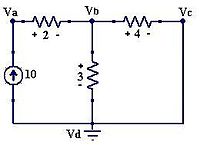
Ejemplo: Del circuito de la figura 4 debemos hallar los voltajes en sus diferentes nodos'
Solución:
- Se localizan todos los nodos del circuito.
- Se busca el nodo con más conexiones y se le llama nodo de referencia Vd (Figura 5).
- No hay fuentes de tensión.
- Se le asignan variables a los nodos Va, Vb y Vc
- Se plantean las ecuaciones según las leyes de Kirchhoff, así:
- Para calcular el voltaje en el nodo Va, decimos que la resistencia de
 tiene la polaridad de la Figura 5. Así
tiene la polaridad de la Figura 5. Así
- Para calcular el voltaje en el nodo Va, decimos que la resistencia de
-

- simplificando:
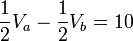
- Para calcular el voltaje en el segundo nodo (Vb) las resistencias que van a dicho nodo tendrán la polaridad de la Figura 6:
- factorizando obtenemos
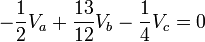
- Para la polaridad del nodo Vc asumimos así:

-
- factorizando obtenemos:

Sistema de ecuaciones: Obtenemos un sistema de ecuaciones del cual podemos determinar los valores del los voltajes en los nodos.

Solucionando el sistema lineal, nos da como resultado los voltajes: 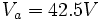 ,
,  y
y 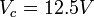
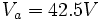 ,
,  y
y 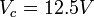
Supernodos
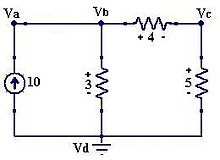
En este circuito, inicialmente tenemos dos tensiones desconocidas, V1 y V2. La tensión en la terminal positiva de VB ya se conoce porque la otra terminal se encuentra en el nodo de referencia. La corriente que pasa por la fuente de voltaje VA no puede ser calculada directamente. Además no podemos escribir las ecuaciones de corriente para V1 y V2. Incluso si los nodos no pueden resolverse individualmente, sabemos que la combinación de estos nodos es cero. Esta combinación de los dos nodos es llamada el método de supernodo, y requiere una ecuación adicional, que involucre las tensiones que afectan a la fuente, V1 = V2 + VA.
El sistema de ecuaciones para este circuito es:

Al sustituir V1 en la primera ecuación y resolviendo con respecto a V2, tenemos: 

Ejemplo de resolución por supernodos
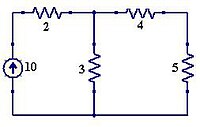
Para calcular la tensión entre las terminales de la fuente de tensión, sumamos las tensiones de las resistencias que están unidas a estos nodos, y además consideramos los dos nodos de la fuente de tensión como uno solo, así:
- Tensión en la resistencia de 4Ω:
- factorizando
- Observamos el supernodo en los nodos
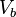 y
y  , tomamos estos dos nodos como uno solo, por lo tanto sumamos las corrientes de las resistencias que hay conectadas a
, tomamos estos dos nodos como uno solo, por lo tanto sumamos las corrientes de las resistencias que hay conectadas a
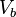 y
y  :
:
- factorizando
- Finalmente, planteamos una ecuación para la fuente de voltaje la cual es la caída de voltaje en los nodos así:
Observación:Debemos tener en cuenta la polaridad de la fuente para plantear esta última ecuación, y así obtener el sistema de ecuaciones para determinar los valores de los voltajes.
Sistema de ecuaciones: 

Resolviendo Va= 62,5 V, Vb= 22,5 V y Vc= 12,5 V







































































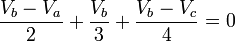
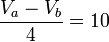



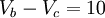
No hay comentarios:
Publicar un comentario