sábado, 23 de abril de 2016

Temas de física

Aceleración

La aceleración es una magnitud física presente en muchos de los fenómenos que nos rodean en la vida diaria, y representa el cambio de la velocidad por unidad de tiempo de un cuerpo de masa m cuando se le aplica una fuerza F. Utilicemos los esquemas de las figuras que siguen para entender su naturaleza.

Supongamos que colocamos un coche de masa m en un camino ideal, liso, horizontal y donde las pérdidas porrozamiento son nulas. (figura1).

Supongamos también, que en ciertos puntos del camino se colocan dos tipos de sensores, tres velocímetros y tres cronómetros. Estos sensores determinarán la velocidad del coche al pasar por los puntos en cuestión y también el tiempo transcurrido desde el inicio del movimiento, los que se indican en las pantallas de cada uno.

En el camino se han marcado las distancias en metros.

El coche está inicialmente detenido sobre el punto de referencia 0.

A este estado de reposo le agregamos el empuje de una fuerza F, el coche comenzará a moverse cada vez mas rápido como se muestra en la figura 2.

A este tipo de movimiento, cuya velocidad cambia constantemente se le llama movimiento acelerado, es decir el cuerpo en cuestión tiene una aceleración.

Observe las indicaciones de los sensores al transcurrir el movimiento del coche. Apóyese en la figura 3, en esta, para facilitar la observación, se ha detenido por un momento el movimiento del coche en los puntos de interés.

Note lo siguiente: 
  1. Durante el primer segundo de tiempo, el coche recorrre una distancia de 5 metros, y la velocidad es de 10 m/seg.
  2. En el próximo segundo de tiempo, la distancia recorrida aumenta a 20 metros, mientras que la  velocidad registrada es de 20 m/seg.
  3. En el tercer segundo de tiempo, la distancia recorrida es mucho mayor, 45 metros, y la velocidad es de 30 m/seg.
Del experimento anterior podemos sacar las conclusiones siguientes:
  1. Cuando a un cuerpo de masa m se le aplica una fuerza constante F, el cuerpo adquiere un movimiento en la misma dirección de la fuerza, y en este movimiento la velocidad del cuerpo cambia constantemente, por lo que es un movimiento acelerado. 
  2. El aumento de velocidad es siempre el mismo por cada unidad de tiempo, esto es, un aumento de 10 m/seg en cada segundo. Lo que hace suponer que la aceleración es constante 10m/seg/seg, o lo que es lo mismo 10 m/seg2.
  3. El cambio de velocidad con respecto al tiempo del movimiento generado se produce en la misma dirección de la fuerza aplicada. Esto nos indica que la aceleración es una magnitud de tipo vectorial, es decir, para establecer su naturaleza exacta es necesario dar dos parámetros, magnitud y dirección.
  4. A medida que pasa el tiempo, el espacio recorrido por unidad de tiempo es cada vez mayor. Primero 5 metros en el primer segundo, luego 20 metros en el próximo y finalmente 45 metros en el tercer segundo. Si se fija, la distancia total recorrida es directamente proporcional al cuadrado del tiempo. Note que al cabo de 2 segundos la distancia total recorrida (20 metros) es cuatro (2²) veces la recorrida en el primer segundo (5 metros) y a los 3 segundos la distancia recorrida (45 metros) es nueve (3²) veces mayor que la del primer segundo.
Ahora hagamos el mismo experimento aplicando al mismo coche una fuerza doble a la utilizada en el experimento anterior, la figura 4 muestra lo que sucede.

En este caso la fuerza de empuje es 2F, doble de la anterior, y el automóvil (masa) es el mismo.

Observemos los resultados, y hagamos una comparación con los resultados del experimento anterior:

Observe que ahora.
  1. Al transcurrir el tiempo los valores de velocidad son dobles en cada instante de tiempo, es decir, el cambio de velocidad por unidad de tiempo se ha duplicado, y como la aceleración es precisamente eso, se desprende que la aceleración se ha duplicado también. Ahora es de 20 m/seg2.
  2. El espacio recorrido, también ha sido doble en cada instante de tiempo, pero manteniendo la condición de tener una relación cuadrática con respecto a este. Note que al cabo de 2 segundos la distancia total recorrida (40 metros) es cuatro (2²) veces la recorrida en el primer segundo (10 metros) y a los 3 segundos la distancia recorrida (90 metros) es nueve (3²) veces mayor que la del primer segundo.
    De esta comparación llegamos a una segunda conclusión importante: La aceleración es proporcional a la fuerza aplicada; si se duplica la fuerza, también se duplica al aceleración.

    Lo contrario sucede si se aumenta la masa m, así por ejemplo, si en lugar de aplicar la fuerza F al coche del primer experimento, la aplicamos a un camión de masa doble a la del coche, los resultados mostrarían que el cambio de velocidad por unidad de tiempo se reduciría a la mitad, y con ello, la aceleración en la misma proporción. Este hecho indica que la magnitud de la aceleración es inversamente proporcional a la masa, lo que significa que para una fuerza constante; a mayor masa menor aceleración y viceversa.

    Como ya hemos entendido qué es la aceleración y como se relaciona con la velocidad, el espacio y la fuerza aplicada, ya estamos en condiciones de expresar matemáticamente los resultados obtenidos. Así tenemos:

    La relación entre la aceleración a, la masa m, y la fuerza F en cualquier momento es:

    F=m.
    		a

    La velocidad v de un cuerpo que parte del reposo con aceleración constante a al transcurrir el tiempo t es:

    v=a.
    		t

    El espacio X recorrido por un cuerpo que parte del reposo con aceleración a en el tiempo t es:

    X=½.
    		a.
    		t²

    Para el caso de que el cuerpo al que se le aplica la fuerza, y con ello una aceleración, ya tuviera una velocidad inicial v0 antes de la aplicación y además no se encuentre en el punto de referencia 0 si no en un punto adelantado X0, las fórmulas mas generales son:

    v=v0+a.t

    X=X0+v0.t+½.a.t2

    esquema
    Figura 1

    animado
    Figura 2

    animadoFigura 3

    animado




    El concepto aceleración, no tiene que ver con ir moviéndose rápido.  Es un concepto que en muchas ocasiones ha sido mal utilizado en la vida real, sin embargo, su significado en física es muy diferente.  Es muy común escuchar que se utiliza este concepto para indicar que un objeto se mueve a gran velocidad lo cual es incorrecto.  El concepto aceleración se refiere al cambio en la velocidad de un objeto. Siempre que un objeto cambia suvelocidad, en términos de su magnitud o dirección, decimos que está acelerando. 
    La Enciclopedia Encarta 2008 explica que la aceleración, se conoce también como aceleración lineal, y es la variación de la velocidad de un objeto por unidad de tiempo.  La velocidad se define como vector, es decir, tiene módulo (magnitud), dirección y sentido. De ello se deduce que un objeto se acelera si cambia su celeridad (la magnitud de la velocidad), su dirección de movimiento, o ambas cosas. Si se suelta un objeto y se deja caer libremente, resulta acelerado hacia abajo. Si se ata un objeto a una cuerda y se le hace girar en círculo por encima de la cabeza con celeridad constante, el objeto también experimenta una aceleración uniforme; en este caso, la aceleración tiene la misma dirección que la cuerda y está dirigida hacia la mano de la persona.
    La aceleración es la razón de cambio en la velocidad respecto al tiempo. Es decir, la aceleración se refiere a cuan rápido un objeto en movimiento cambia su velocidad. Por ejemplo, un objeto que parte de reposo y alcanza una velocidad de 20 km/h, ha acelerado.  Sin embargo, si a un objeto le toma cuatro segundos en alcanzar la velocidad de 20 km/h, tendrá mayor aceleración que otro objeto al que le tome seis segundos en alcanzar tal velocidad.

    Definimos la aceleración como el cambio en la velocidad respecto al tiempo durante el cual ocurre el cambio. El cambio en la velocidad (ΔV) es igual a la diferencia entre la velocidad final (Vf)y la velocidad inicial (Vi). Esto es: 

    Por lo tanto definimos la aceleración matemáticamente como:

    De la ecuación surge la posibilidad de que la aceleración sea positiva o negativa. La aceleración resulta ser positiva si el objeto aumentara su velocidad. Cuando el objeto aumenta la velocidad, entonces la velocidad final sería mayor que la inicial por lo que al restarlas para determinar la diferencia, la misma sería positiva. Por el contrario, si el objeto disminuye lavelocidad, entonces la aceleración sería negativa. La velocidad final sería menor que la inicial y por tanto la diferencia entre ambas sería negativa. En ambos casos, si la velocidad aumenta o disminuye, decimos que el objeto está acelerado. Sin embargo es muy común utilizar la palabra desaceleración para referirnos a la aceleración negativa. 
    0 - 60 in seven seconds flat. by Reynolds, DanEl signo de la aceleración indica la dirección de la misma. Una aceleración positiva indica que la aceleración es en dirección al movimiento del objeto. La aceleración negativa indica que la misma es en dirección opuesta al movimiento del objeto. En próximas lecciones profundizaremos más en este aspecto.
     
    Si ocurriera que la velocidad final y la inicial son iguales, entonces la aceleración sería igual a cero. Para que la velocidad final y la inicial sean iguales, el objeto tendría que moverse con velocidad constante. Por lo tanto, los objetos que se mueven con velocidad constante tienen una aceleración igual a cero.
    Ahora, imagina un auto que se mueve alrededor de una pista circular. Si el chófer mantiene el velocímetro, digamos que en 20 mph, el auto se estaría moviendo con rapidez constante; pero su velocidad no lo sería. Recuerda que aceleración se refiere a un cambio en la magnitud o en la dirección de la velocidad. Si el auto se mueve en una pista circular, la dirección de la velocidad cambia constantemente con la posición del auto en la pista. Por tal motivo, decimos que aunque la magnitud de la velocidad sea constante (la rapidez), la dirección de la velocidad no lo es. Por tanto, el auto estaría acelerando.
     
    La unidad para medir la aceleración según el Sistema Internacional de Medidas es el metro por segundo cuadrado (m/s²). Recuerda que el cambio en la velocidad se mide en m/s y al dividir esta unidad por el tiempo en segundos resulta (m/s)/s o m/s². 
     
     
    Cuando conocemos la aceleración de un objeto, y esta es uniforme, podemos determinar su velocidad al cabo de un intervalo de tiempo. Para ello, resolveremos la ecuación de la definición de aceleración para la velocidad final.

     Si
    Esta ecuación puede ser escrita así también:



     
     
     
     
    En la pasada lección discutimos que para un objeto que se mueve con velocidad constante (a = 0), la gráfica de posición versus tiempo resulta ser una línea recta, como lo muestra la figura de la derecha.  Observa el diagrama de puntos que aparece en la parte izquierda de la gráfica.  Se puede observar que la distancia entre ellos es muy similar.
     
     
     
     
     
     
     
     
     
     
     
    Si por el contrario el objeto se mueve con aceleración uniforme distinta de cero, entonces la gráfica de posición versus tiempo resulta ser una parábola.Ese es el caso de la imagen de la derecha.  En esta puedes observar que la distancia entre los puntos va aumentando más cada vez y por lo que esa distancia no es uniforme.


    En este caso, el objeto se aleja del origen aumentando la velocidad uniformemente. El aumento uniforme en la velocidad, hace que el objeto recorra mayor distancia por unidad de tiempo según se aleja. Por ello, la gráfica resulta ser una parabólica. Observa que el cambio en la posición al principio es pequeño y el mismo va aumentando según pasa el tiempo. 
     
    Si determinamos la velocidad instantánea del objeto cada segundo, observaríamos un aumento proporcional en la misma. Por lo que la gráfica de velocidad versus tiempo sería una lineal con lapendiente igual a la aceleración.  Puedes repasar estos conceptos en la unidad de Análisis gráfico del movimiento.


    La aceleración es la magnitud física que mide la tasa de variación de la velocidad respecto del tiempo. Las unidades para expresar la aceleración serán unidades de velocidad divididas por las unidades de tiempo (en unidades del Sistema Internacional se usa generalmente) para la física
    No debe confundirse la velocidad con la aceleración, pues son conceptos distintos, acelerar no significa ir más rápido, sino cambiar de velocidad.
    Se define la aceleración media como la relación entre la variación o cambio de velocidad de un móvil y el tiempo empleado en dicho cambio:
    a= \frac{v-v_0}{t-t_0} = \frac{\Delta v}{\Delta t}
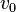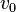    Donde a es aceleración, y v la velocidad final en el instante t,  v_0  la velocidad inicial en el instante t0.
    Aceleración instantánea.
    La aceleración instantánea, que para trayectorias curvas se toma como un vector, es la derivada de la velocidad (instantánea) respecto del tiempo en un instante dado (en dos instantes cercanos pero diferentes el valor puede cambiar mucho):
    \mathbf{a}=\frac{d\mathbf{v}}{dt}
    Puesto que la velocidad instantánea v a su vez es la derivada del vector de posición r respecto al tiempo, se tiene que la aceleración vectorial es la derivada segunda respecto de la variable temporal:
    \mathbf{a} = \frac{d^2 \mathbf{r}}{dt^2}

    Componentes intrínsecas de la aceleración: aceleraciones tangencial y normal

    Existe una descomposición geométrica útill del vector de aceleración de una partícula, en dos componentes perpendiculares: la aceleración tangencial y la aceleración normal. La primera da cuenta de cuanto varía el módulo del vector velocidad o celeridad. La aceleración normal por el contrario da cuenta de la tasa de cambio de la dirección velocidad:
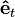    \mathbf{a}= \frac{d\mathbf{v}}{dt} = \frac{d}{dt}(\left \Vert \mathbf{v} \right \|\mathbf{\hat{e}}_t) = \frac{d\left \Vert \mathbf{v} \right \|}{dt}\mathbf{\hat{e}}_t + \left \Vert \mathbf{v} \right \|\frac{d\mathbf{\hat{e}}_t}{dt} = a_t \mathbf{\hat{e}}_t + \left \Vert \mathbf{v} \right \| (\boldsymbol{\omega} \times \hat{e}_t)

    Donde \mathbf{\hat{e}}_t es el vector unitario y tangente a la trayectoria del mismo sentido que la velocidad. Usando las fórmulas de geometría diferencial de curvas se llega a que la expresión anterior es igual a:
    \mathbf{a}= \frac{d\mathbf{v}}{dt} = a_t \mathbf{\hat{e}}_t + \frac{\left \Vert \mathbf{v} \right \|^2}{\rho} \mathbf{\hat{e}}_n = a_t \mathbf{\hat{e}}_t + a_n \mathbf{\hat{e}}_n

    Donde at es la aceleración tangencial, an es la aceleración normal y los vectores que aparecen en la anterior expresión se relacionan con los vectores del Triedro de Frênet-Serret que aparece en la geometría diferencial de curvas del siguiente modo:
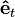    \mathbf{\hat{e}}_t es el vector unitario tangente a la curva.
    \mathbf{\hat{e}}_n es el vector normal (unitario) de la curva.
    \boldsymbol{\omega} es el vector velocidad angular que es siempre paralelo al vector binormal de la curva.
    Publicado por en

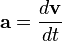
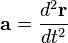
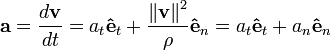
    No hay comentarios:

    Publicar un comentario

    Suscribirse a: Enviar comentarios (Atom)